一、二叉搜索树概念

二叉搜索树又叫二叉排序数，它或者是空树，或者是具有以下性质的二叉树：

1. 如果它的左子树不为空，那么左子树上所有节点的值都小于根结点的值。
2. 如果它的右子树不为空，那么右子树上所有节点的值都大于根节点的值。
3. 它的左右子树也是二叉搜索树。

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

比如说：这个数组都可以将它化为二叉搜索树

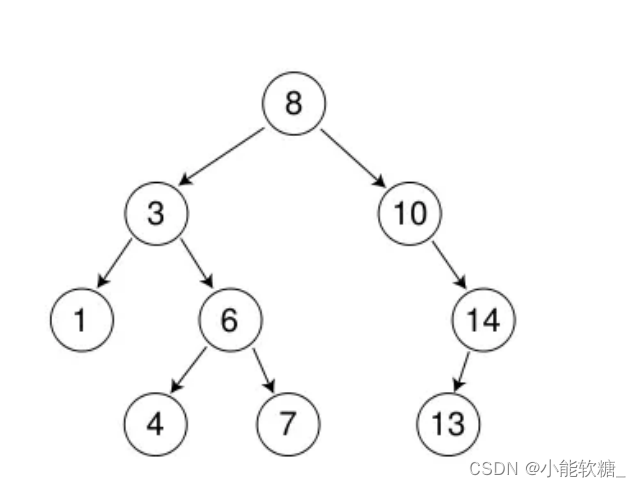
总结：在左子树值比根小，右子树值比根大。 当树走中序遍历时，序列都是有序的。

二叉搜索树 的 结构定义：

#include<iostream>
using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
private:Node* _root;
public:BSTree():_root(nullptr){}
};

二、二叉搜索树操作（非递归）

1.二叉搜索树的查找 （非递归）

利用二分查找的方法，借助我们去二叉搜索树中查找节点。

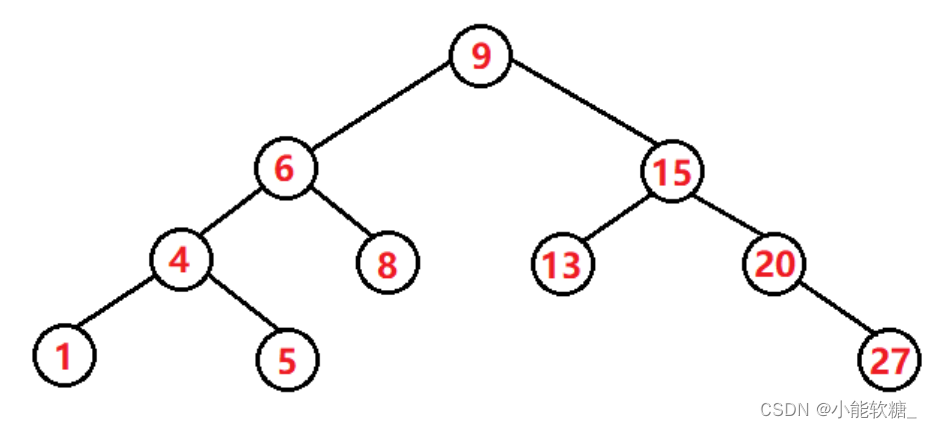
查找的时间复杂度：最坏的情况，就是查找高度（h=logN）次，就可以判断一个值在不在节点里面。

（1）查找

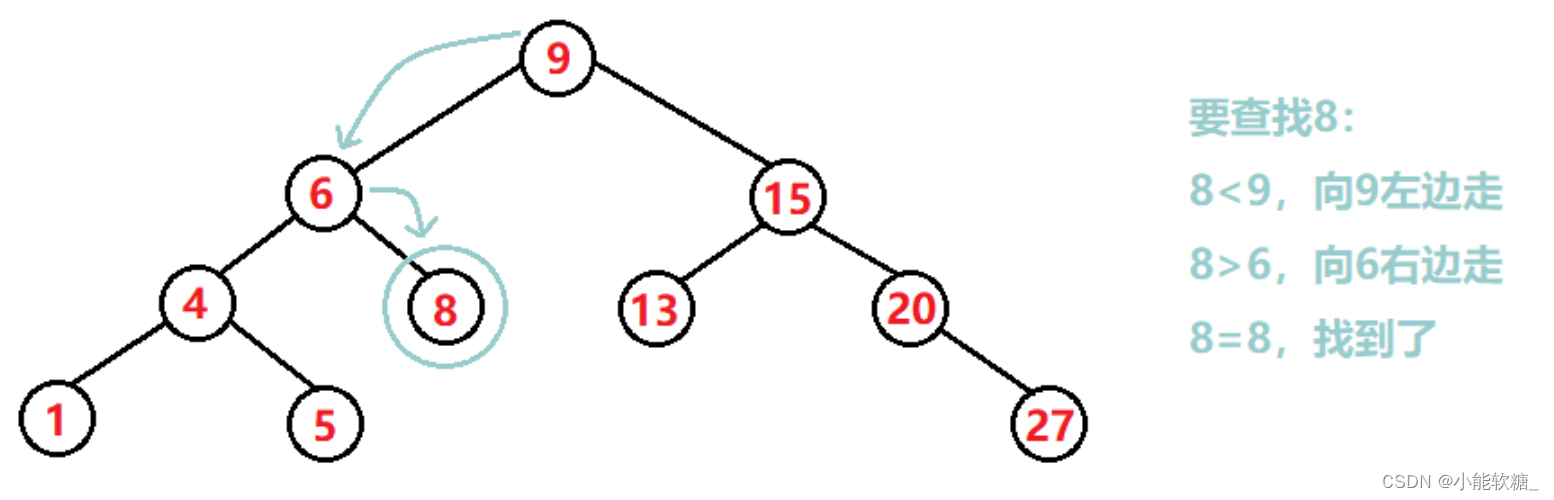
查找的思路：

1. key比当前结点的值小，往左走！
2. key比当前结点的值大，往右走！
3. key==当前结点的值，就找到了！

// 查找：Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;// 找到了！}}return nullptr;// 遍历完了，都还没找到！}

（2）中序遍历

由于根节点_root是私有成员变量，如果在main函数里面来进行中序遍历的话，这就是在类外对私有成员进行访问，这是不合法的！

所以说我们要解决这个问题，可以用这样：
在类的public内的 中序遍历 InOrder 里面 再套一层私有的中序遍历：_InOrder，这样，_InOrder身为私有函数，就可以访问：私有变量_root！

private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << endl;_InOrder(root->_right);}
public:// 中序遍历：void InOrder() //这个函数 类外可以直接访问！{_InOrder(_root); // 这个函数，是 私有函数 对 私有成员 的访问！cout << endl;}

2.二叉搜索树的插入（非递归）

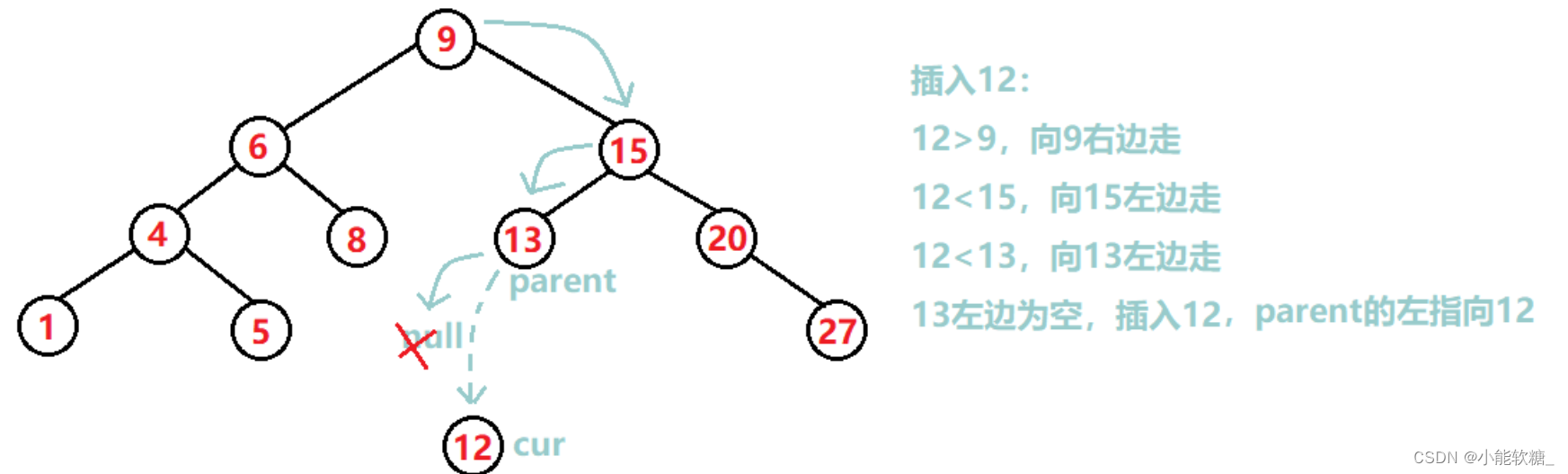
插入节点分两步：

（1）找位置

    ①key比当前节点值大，向左走②key比当前节点值小，向右走③key等于当前节点值，该节点值已经存在，插入失败

（2）插入

    ①key比父亲节点值小就插入父亲左子树②key比父亲节点值大就插入父亲右子树

由于插入后，要将节点链接到树中，因此要定义parent节点，用来链接新节点：

// 插入：bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;// (1) 找到插入的位置while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;// 二叉搜索树不允许数据冗余！}}cur = new Node(key);// (2) 判断if (key<parent->_key){parent->_left = cur;}else{parent->_right = cur;}return true;}

3.二叉搜索树的删除（非递归）

非递归删除：

（1）找位置

    ①key比当前节点值大，向左走②key比当前节点值小，向右走③key等于当前节点值，找到了，准备删除

（2）删除，有两种删除方法：非递归和递归

    非递归删除: ①该节点没有孩子，即该节点是叶子节点，删除节点后把父亲指向自己的指针置空

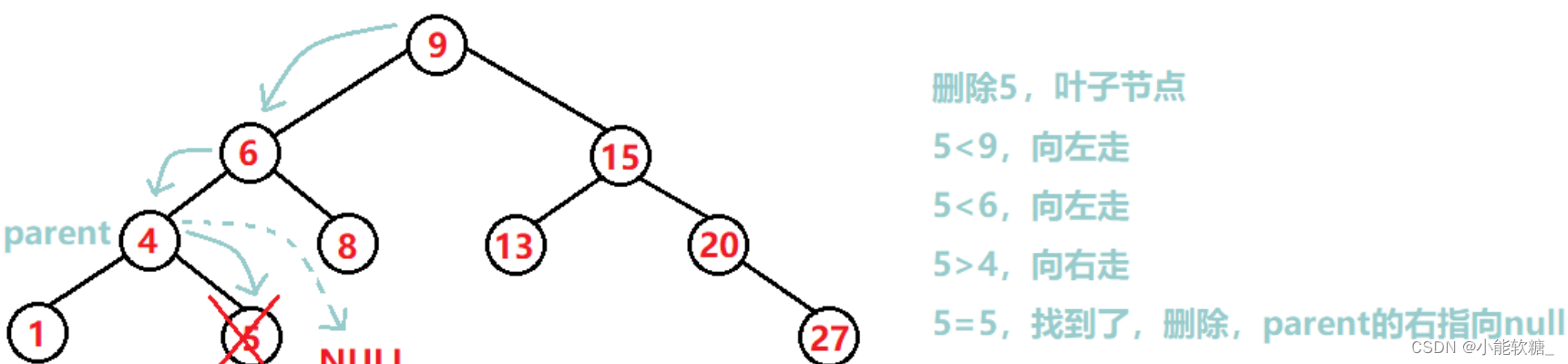
    ②该节点有一个孩子，就把该节点的孩子节点的链接给该节点的父亲，顶替自己的位置，①可以当成②的特殊情况

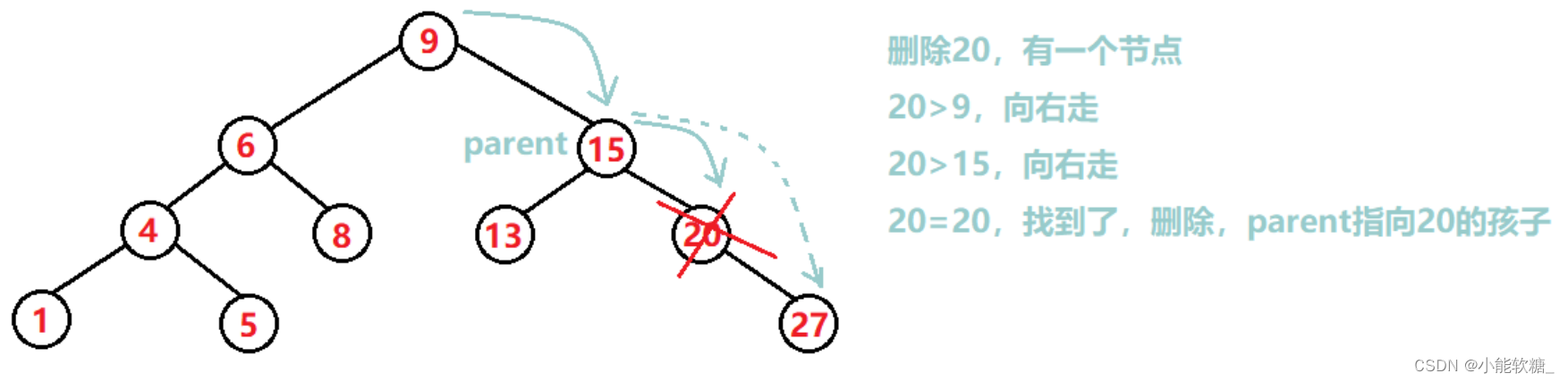
    ③该节点有两个孩子，找比它自己的左孩子大，比它自己的右孩子小的节点替换它（也就是拿它的左子树的最大节点或右子树的最小节点替换它），替换之后，该节点就只有一个孩子或没有孩子了，就变成①或②了。

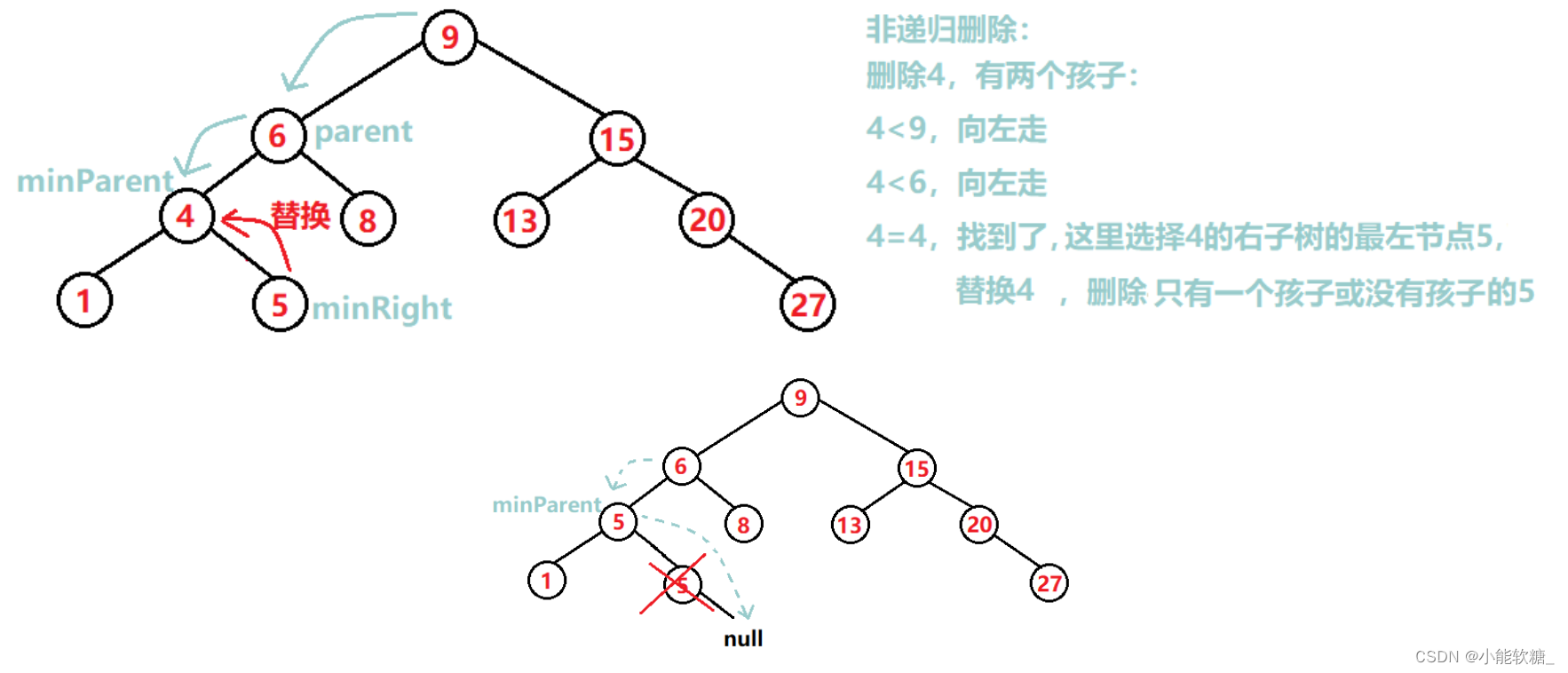
// 删除bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;// (1) 找到插入的位置while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{break;}}// 1、2、 (子 代替 父亲的位置)// 大前提：如果要删除的节点，left为空if (cur->_left == nullptr){// 如果要删除根！if (cur == _root){_root = cur->_right;// 那就让cur的右当根}// 如果要删除的不是根！else{// 如果要删除的节点cur，在父亲的左边。// 因为是替代法，所以说要让 子 的位置代替 父亲 的位置，但是 子 的位置只有_right存在，所以说会把_right的位置放到即将要删除cur的位置。if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}// 大前提：如果要删除的节点，right为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 因为是替代法，所以说要让 子 的位置代替 父亲 的位置，但是 子 的位置只有_left存在，所以说会把_left的位置放到即将要删除cur的位置。if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}// 3、要删除的cur不只有一个节点。可能有多个节点，甚至整个指子树// 找到要删除节点cur，左子树最大的节点，右子树最小的节点，来代替cur的位置。else{// 要么找cur左子树中的max，要么就找右子树中的min// 这里 以 RightMin为例！// (1)找到 RightMin (就像找 cur那样)Node* RightMin = cur->_right;Node* RightMinParent = cur; // 定义 RightMinParent 为了方便后续节点的连接。while (RightMin->_left){RightMinParent = RightMin;RightMin = RightMin->_left;}// (2)找到了 就交换！swap(RightMin->_key, cur->_key);// (3) 交换完后 就链接！if (RightMinParent->_left == RightMin)RightMinParent->_left = cur;elseRightMinParent->_right = cur;// 链接完成！delete cur;}return true;}

递归删除：

相对于非递归，只需要修改找到了要修改的代码：找到了后不需要管cur到底左为空、右为空、还是左右都不为空

① 找要删除节点的右子树的最小节点并把它的值保存起来

② 删除右子树的最小节点

③ 把要删除的节点值替换成右子树的最小节点值

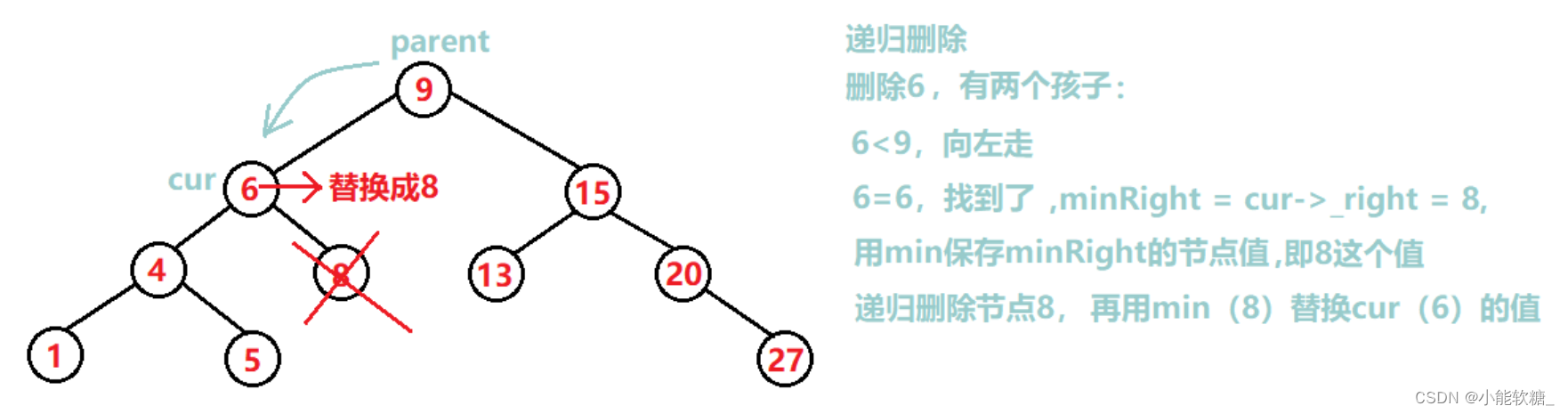
                else//左右都不为空，替换法删除{//找右子树最小节点Node* minRight = cur->_right;while (minRight->_left){minRight = minRight->_left;}//用min保存右子树最小节点的值K min = minRight->_key;//递归调用自己去替换删除节点，一定会走到左为空的情况处理this->Erase(min);//删除完毕替换节点之后，把cur的值替换成mincur->_key = min;}

三、二叉搜索树操作（递归）

理解了非递归操作以后， 递归操作就很简单了：

#include<iostream>
using namespace std;//树的节点可以支持多种类型
template<class K>
//树节点结构
struct BSTreeNode
{BSTreeNode<K>* _left;//左指针BSTreeNode<K>* _right;//右指针K _key;//值//构造函数BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BStree//树结构
{typedef BSTreeNode<K> Node;
public://递归查找Node* FindR(const K& key){return _FindR(_root, key);}//递归插入bool InsertR(const K& key){return _InsertR(_root, key);}//递归删除bool EraseR(const K& key){return _EraseR(_root, key);}
private:Node* _root;
};

由于_root是私有的，可以把递归子函数查找、插入、删除都定义成私有的

1.二叉搜索树的查找（递归）

private://查找Node* _FindR(Node* root, const K& key){if (root == nullptr)//没找到{return nullptr;}if (key < root->_key)//到左子树去找{FindR(root->_left, key);}else if (key > root->_key)//到右子树去找{FindR(root->_right, key);}else//找到了{return root;}}

2.二叉搜索树的插入（递归）

	//插入 加了&，root是_root的别名，修改root就直接修改到上一层调用，不用找父亲bool _InsertR(Node*& root, const K& key){if (root == nullptr)//找到位置了{root = new Node(key);return true;}if (key < root->_key)//到左子树去找位置{_InsertR(root->_left, key);}else if (key > root->_key)//到右子树去找位置{_InsertR(root->_right, key);}else//已存在，无需插入{return false;}}

3.二叉搜索树的删除（递归）

递归删除：和二叉树的删除（非递归）一样，找到后的删除也有两种方式，递归和非递归

找到后的非递归删除：

    //插入 加了&，root是_root的别名，修改root就直接修改到上一层调用，不用找父亲	bool _EraseR(Node*& root, const K& key){if (root == nullptr)//没找到{return false;}if (key < root->_key)//到左子树去找{_EraseR(root->_left, key);}else if (key > root->_key)//到右子树去找{_EraseR(root->_right, key);}else{//找到了，root就是要删除的节点if (root->_left == nullptr)//root左为空{Node* del = root;root = root->_right;delete del;}else if (root->_right == nullptr)//root右为空{Node* del = root;root = root->_left;delete del;}else//root左右都不为空{//找到右子树最左节点替换Node* minParent = root;Node* minRight = root->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}//保存替换节点的值cur->_key = minRight->_key;//链接if (minParent->_left == minRight){minParent->_left = minRight->_right;}else{minParent->_right = minRight->_right;}//删除delete minRight;}return true;}}

找到后的递归删除：

			else//root左右都不为空{				//找右子树最左节点Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}//保存右子树最左节点的值K min = minRight->_key;//使用递归方法删除右子树最左节点_Erase(root->_right, min);}

四、二叉搜索树的默认成员函数

现在还剩下二叉搜索树的构造、拷贝构造、赋值运算符重载、析构函数。

1.构造

public://构造函数需要将根初始化为空就行了BSTree():_root(nullptr){}

2.拷贝构造

拷贝构造利用递归调用子函数不断拷贝节点:

	//拷贝构造BSTree(const BSTree<K>& t){_root = t.copy(t._root);}

在子函数处:

	Node* _copy(Node* root){if (root == nullptr)//如果根为空，直接返回{return;}Node* copyNode = new Node(root->_key);//创建根节点copyNode->_left = _copy(root->_left);//递归拷贝左子树节点copyNode->_right = _copy(root->_right);//递归拷贝右子树节点return copyNode;//返回根}

3.赋值运算符重载

借助拷贝构造用现代写法写:

	//赋值运算符重载(现代写法)BSTree& operator=(const BSTree<K>& t){swap(_root,t._root);return *this;}

4.析构

递归调用子函数去析构

	//析构~BSTree(){_Destroy(_root);_root = nullptr;}

在子函数处:

	_Destroy(root){if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;}

五、K模型和KV模型搜索树

1.K模型搜索树

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
1、以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
2、在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

2.KV模型搜索树

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见：

1、比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；
2、再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对。

改造二叉搜索树为KV结构的代码

#pragma once
#include<iostream>
#include<string>
using namespace std;namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;// pair<K, V> _kv;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:// logNbool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return cur;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空，父亲指向我的右if (cur->_left == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_left;}else{// 右为空，父亲指向我的左if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空，替换法删除// // 查找右子树的最左节点替代删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_key, rightMin->_key);if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};

六、二叉搜索树性能分析

---

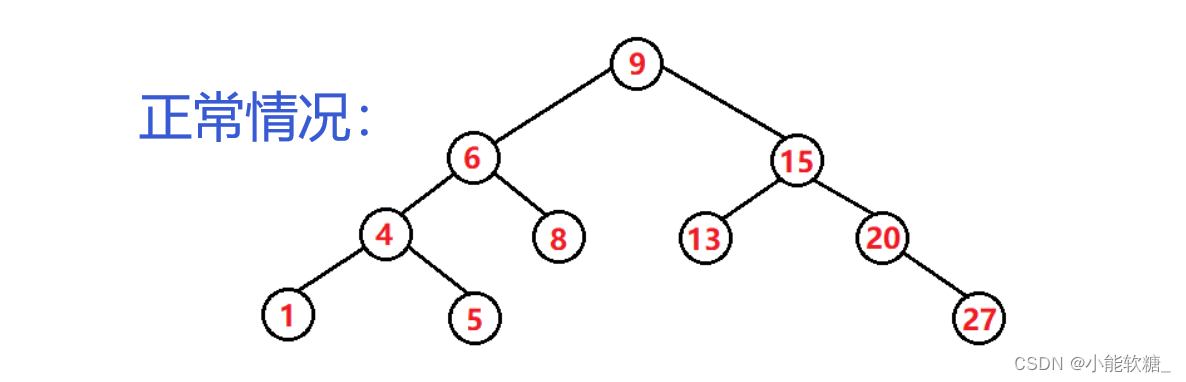
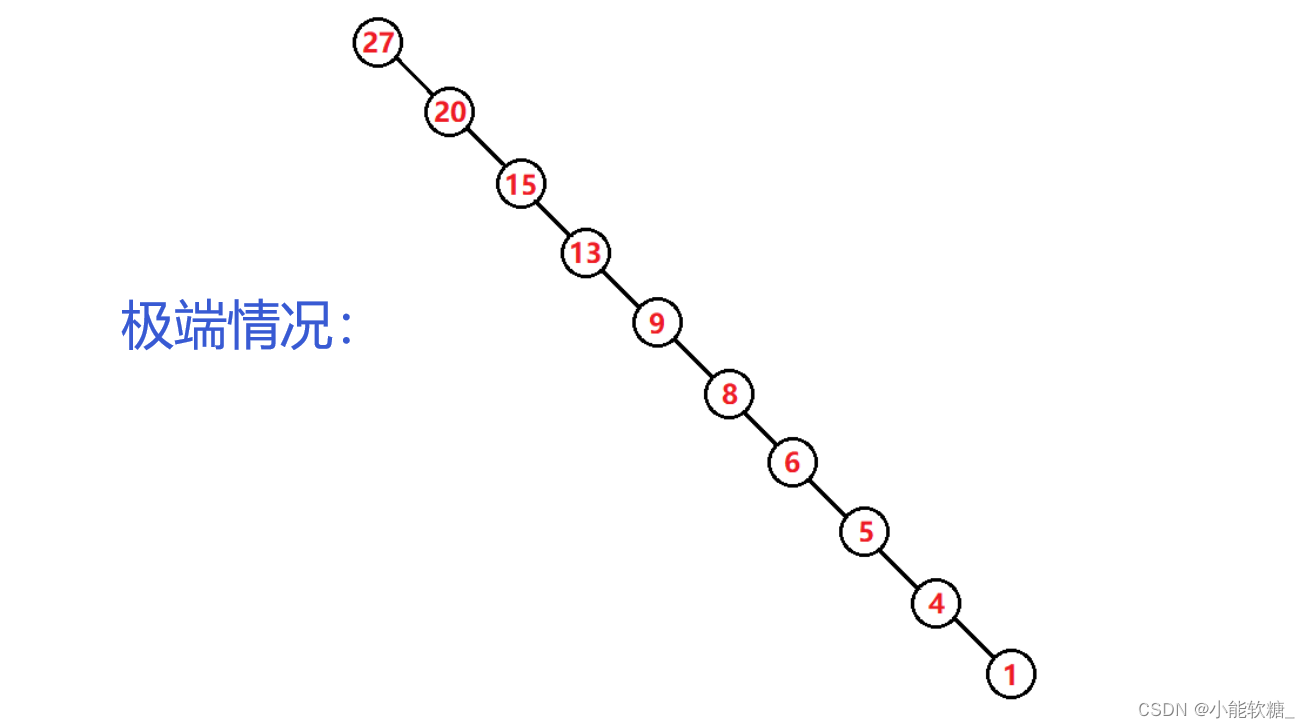
好了，今天的分享就到这里了
如果对你有帮助，记得点赞👍+关注哦！
我的主页还有其他文章，欢迎学习指点。关注我，让我们一起学习，一起成长吧！