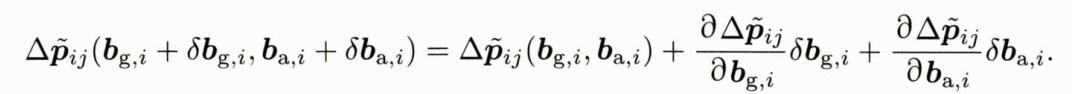IMU状态预积分代码实现 —— IMU状态预积分类
- 实现IMU状态预积分类
实现IMU状态预积分类
首先,实现预积分自身的结构。一个预积分类应该存储一下数据:
- 预积分的观测量 △ R ~ i j , △ v ~ i j , △ p ~ i j \bigtriangleup \tilde{R} _{ij},\bigtriangleup \tilde{v} _{ij},\bigtriangleup \tilde{p} _{ij} △R~ij,△v~ij,△p~ij
- 预积分开始时的IMU零偏 b g , b a b_{g},b_{a} bg,ba
- 在积分时期内的测量噪声 Σ i , k + 1 \Sigma _{i,k+1} Σi,k+1
- 各积分量对IMU零偏的雅克比矩阵
- 整个积分时间 △ t i j \bigtriangleup t_{ij} △tij
以上都是必要的信息。除此之外,也可以将IMU的读数记录在预积分类中(当然,也可以不记录,因为都已经积分过了)。同时,IMU的测量噪声和零偏随机游走噪声也可以作为配置参数,写在预积分类中。
声明这个类
class IMUPreintegration {
参数配置项
其中包括:
- 陀螺仪初始零偏
- 加速度计初始零偏
- 陀螺噪声
- 加计噪声
/// 参数配置项/// 初始的零偏需要设置,其他可以不改struct Options {Options() {}Vec3d init_bg_ = Vec3d::Zero(); // 初始零偏Vec3d init_ba_ = Vec3d::Zero(); // 初始零偏double noise_gyro_ = 1e-2; // 陀螺噪声,标准差double noise_acce_ = 1e-1; // 加计噪声,标准差};
构造函数
IMUPreintegration(Options options = Options());
中间省略函数的声明,之后再写。
下面完成类的成员变量定义
整体预积分时间
double dt_ = 0; // 整体预积分时间
噪声矩阵,累积噪声矩阵 Σ i , k + 1 \Sigma _{i,k+1} Σi,k+1 ,测量噪声矩阵 C o v ( η d , k ) Cov(\eta_{d,k} ) Cov(ηd,k)
Mat9d cov_ = Mat9d::Zero(); // 累计噪声矩阵Mat6d noise_gyro_acce_ = Mat6d::Zero(); // 测量噪声矩阵
预积分开始时的IMU零偏 b g , b a b_{g},b_{a} bg,ba
// 零偏Vec3d bg_ = Vec3d::Zero();Vec3d ba_ = Vec3d::Zero();
预积分的观测量 △ R ~ i j , △ v ~ i j , △ p ~ i j \bigtriangleup \tilde{R} _{ij},\bigtriangleup \tilde{v} _{ij},\bigtriangleup \tilde{p} _{ij} △R~ij,△v~ij,△p~ij
// 预积分观测量SO3 dR_;Vec3d dv_ = Vec3d::Zero();Vec3d dp_ = Vec3d::Zero();
各积分量对IMU零偏的雅克比矩阵
// 雅可比矩阵Mat3d dR_dbg_ = Mat3d::Zero();Mat3d dV_dbg_ = Mat3d::Zero();Mat3d dV_dba_ = Mat3d::Zero();Mat3d dP_dbg_ = Mat3d::Zero();Mat3d dP_dba_ = Mat3d::Zero();
因为IMU零偏相关的噪声项并不直接和预积分类有关,所以将它们挪到优化类当中。这个类主要完成对IMU数据进行预积分操作,然后提供积分之后的观测量与噪声值。
下面来看单个IMU的积分函数,首先在类中进行声明。
/*** 插入新的IMU数据* @param imu imu 读数* @param dt 时间差*/void Integrate(const IMU &imu, double dt);
来看函数具体实现
整体而言,它按照以下顺序更新内部的成员变量:
- 更新位置和速度的测量值
- 更新运动模型的噪声矩阵
- 更新观测量对零偏的各雅克比矩阵
- 更新旋转部分的测量值
- 更新积分时间在这里插入代码片
void IMUPreintegration::Integrate(const IMU &imu, double dt) {
去掉零偏的测量
Vec3d gyr = imu.gyro_ - bg_; // 陀螺Vec3d acc = imu.acce_ - ba_; // 加计
更新预积分速度观测量和位置观测量
// 更新dv, dpdp_ = dp_ + dv_ * dt + 0.5f * dR_.matrix() * acc * dt * dt;dv_ = dv_ + dR_ * acc * dt;
对应公式为
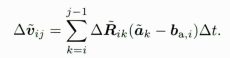
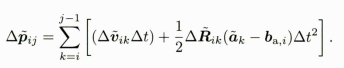
预积分旋转观测 dR先不更新,因为A, B阵还需要现在的dR
下面计算运动方程雅克比矩阵系数A、B阵,用于更新噪声项
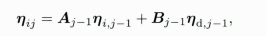
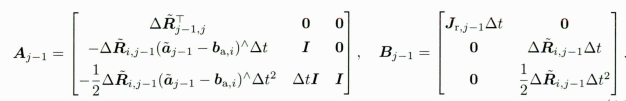
// 运动方程雅可比矩阵系数,A,B阵,// 另外两项在后面Eigen::Matrix<double, 9, 9> A;A.setIdentity();Eigen::Matrix<double, 9, 6> B;B.setZero();
加速度计的伴随矩阵和t的平方
Mat3d acc_hat = SO3::hat(acc);double dt2 = dt * dt;
公式中的这个地方有用到,避免重复计算
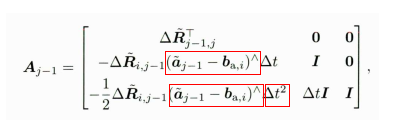
A.block<3, 3>(3, 0) = -dR_.matrix() * dt * acc_hat;A.block<3, 3>(6, 0) = -0.5f * dR_.matrix() * acc_hat * dt2;A.block<3, 3>(6, 3) = dt * Mat3d::Identity();
计算A矩阵中对应的各个块,分别对应公式如下,A矩阵中的A.block<3, 3>(0, 0)块,之后用更新完的dR 更新
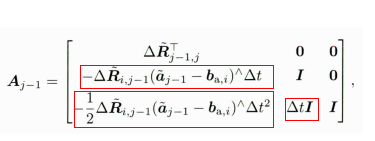
B.block<3, 3>(3, 3) = dR_.matrix() * dt;B.block<3, 3>(6, 3) = 0.5f * dR_.matrix() * dt2;
更新B矩阵的各块,分别对应公式如下
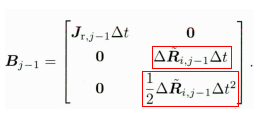
// 更新各雅可比dP_dba_ = dP_dba_ + dV_dba_ * dt - 0.5f * dR_.matrix() * dt2; dP_dbg_ = dP_dbg_ + dV_dbg_ * dt - 0.5f * dR_.matrix() * dt2 * acc_hat * dR_dbg_; dV_dba_ = dV_dba_ - dR_.matrix() * dt; dV_dbg_ = dV_dbg_ - dR_.matrix() * dt * acc_hat * dR_dbg_;
更新各雅克比矩阵对应公式依次为:
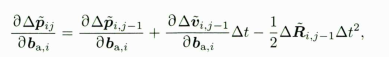

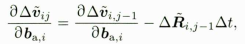
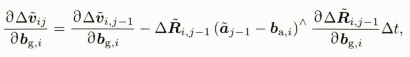
下面更新预积分旋转部分观测量
// 旋转部分Vec3d omega = gyr * dt; // 转动量Mat3d rightJ = SO3::jr(omega); // 右雅可比SO3 deltaR = SO3::exp(omega); // exp后dR_ = dR_ * deltaR; // 更新预积分旋转部分观测量
对应公式:
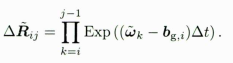
其中右雅克比矩阵的计算是为了更新上面的B矩阵
A.block<3, 3>(0, 0) = deltaR.matrix().transpose();B.block<3, 3>(0, 0) = rightJ * dt;
利用更新完的dR和右雅克比矩阵更新A、B阵中对应的块
对应公式:
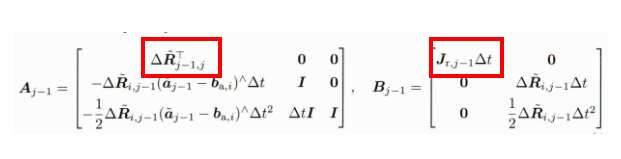
// 更新噪声项cov_ = A * cov_ * A.transpose() + B * noise_gyro_acce_ * B.transpose();
利用填充好的A阵和B阵,来更新噪声项
对应公式如下:
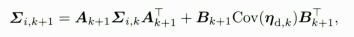
其中 C o v ( η d , k ) Cov(\eta_{d,k} ) Cov(ηd,k)即代码中的noise_gyro_acce_的构成就是陀螺仪和加计的噪声构成的对角矩阵,在构造函数中构成的
const float ng2 = options.noise_gyro_ * options.noise_gyro_;const float na2 = options.noise_acce_ * options.noise_acce_;noise_gyro_acce_.diagonal() << ng2, ng2, ng2, na2, na2, na2;
下则继续更新预积分旋转观测量对陀螺仪零偏的雅克比矩阵
// 更新dR_dbgdR_dbg_ = deltaR.matrix().transpose() * dR_dbg_ - rightJ * dt;
对应公式如下:
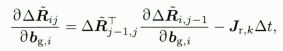
最后增加积分时间:
// 增量积分时间dt_ += dt;
这样就完成了一次对IMU数据的操作。需要注意的是,如果不进行优化,则预积分和直接积分的效果是完全一致的,都是将IMU数据一次性地积分。在预积分之后,也可以向ESKF一样,从起始状态向最终状态进行预测。
预测函数实现如下:
/*** 从某个起始点开始预测积分之后的状态* @param start 起始时时刻状态* @return 预测的状态*/NavStated IMUPreintegration::Predict(const sad::NavStated &start, const Vec3d &grav) const {SO3 Rj = start.R_ * dR_;Vec3d vj = start.R_ * dv_ + start.v_ + grav * dt_;Vec3d pj = start.R_ * dp_ + start.p_ + start.v_ * dt_ + 0.5f * grav * dt_ * dt_;auto state = NavStated(start.timestamp_ + dt_, Rj, pj, vj);state.bg_ = bg_;state.ba_ = ba_;return state;}
与ESKF不同的是,预积分可以对多个IMU数据进行预测,可以从任意起始时刻向后预测,而ESKF通常只在当前状态下,针对单个IMU数据,向下一时刻预测。
获取修正之后的观测量,bias可以与预积分时期的不同,会有一阶修正
// 预积分旋转零偏更新修正后测量值
SO3 IMUPreintegration::GetDeltaRotation(const Vec3d &bg) { return dR_ * SO3::exp(dR_dbg_ * (bg - bg_)); }
对应公式为:
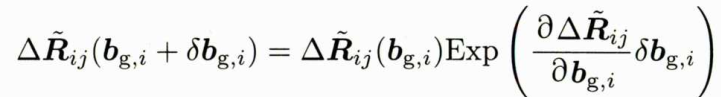
预积分速度零偏更新修正后测量值
// 预积分速度零偏更新修正后测量值Vec3d IMUPreintegration::GetDeltaVelocity(const Vec3d &bg, const Vec3d &ba) {return dv_ + dV_dbg_ * (bg - bg_) + dV_dba_ * (ba - ba_);}
对应公式为:

预积分位置零偏更新修正后测量值
// 预积分位置零偏更新修正后测量值Vec3d IMUPreintegration::GetDeltaPosition(const Vec3d &bg, const Vec3d &ba) {return dp_ + dP_dbg_ * (bg - bg_) + dP_dba_ * (ba - ba_);}
对应公式为: