一、堆的概念

  堆的概念：一个按照完全二叉树的储存方式存储的一维数组我们称之为堆。


  堆可以分为大堆和小堆：
  大堆：二叉树中父亲节点的值都比自己的孩子节点的值大；
  小堆：二叉树中父亲节点的值都比自己的孩子节点的值小；

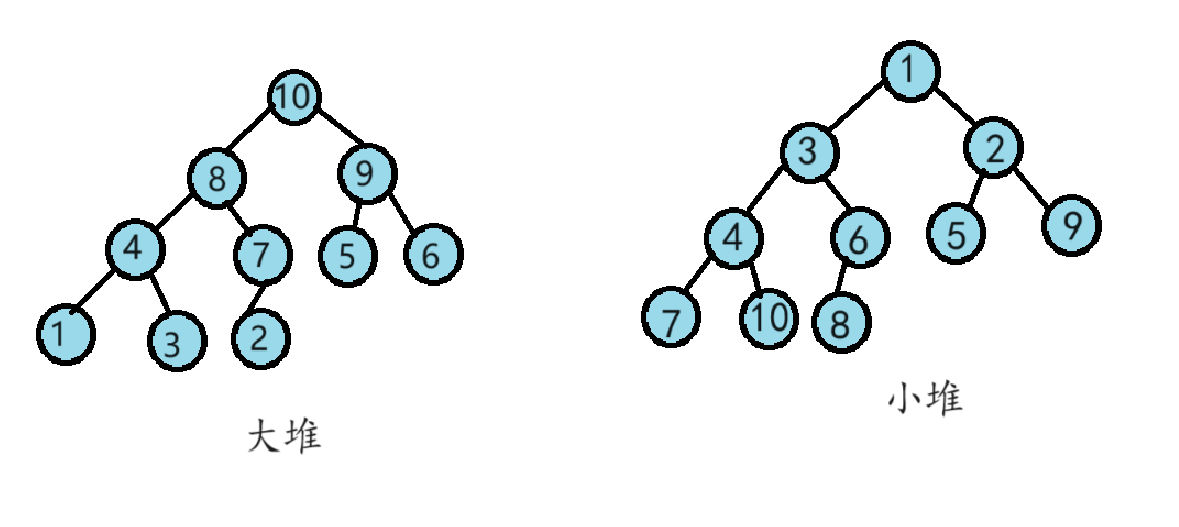
  这就是很明显的一组大小堆。
  堆排序的实现就是在对的基础上完成的。

二、向下调整法

  实现堆排序，用向下调整法时间复杂度最低
下面是向下调整的代码：

void Swap(int* x, int* y)
{int ret = *x;*x = *y;*y = ret;
}//降序建小堆
//升序建大堆
void AdjustDown(int* arr, int n, int father)
{                 // arr为数组 n为数组元素个数  father为当前数组下标//假设左孩子大int child = 2 * father + 1;while (child < n)//结束条件为到达了最后一层，最后一层没有孩子{//比较左右孩子，找出最大的孩子//if (child + 1 < n && arr[child + 1] < arr[child])//小堆， 降序if (child + 1 < n && arr[child + 1] > arr[child])//大堆， 升序{   //child+1<n是为了防止数组越界，    child++; //如果右孩子大于（小于）左孩子，child就加1}//if (arr[father] > arr[child])//小堆， 降序if (arr[father] < arr[child])//大堆， 升序 {Swap(&arr[father], &arr[child]);//father的值小于child的值，让二者交换father = child;  //再次进行下一组的交换，重新定义father和childchild = 2 * father + 1;}else{break;}}}

  以上就是向下调整法建大/小堆的过程。

三、堆排序

  建好堆以后就开始进行排序了，即将此时堆里的数值从上向下梳理一遍，使其变的有序。

  后面我们以大堆排升序为例进行讲解。

建堆

自定义一个函数HeapSort,用来进行堆排序

void HeapSort(int* arr, int n)
{//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--) //(n - 1 - 1) / 2是最后一个有孩子的父节点{AdjustDown(arr, n, i);}
}

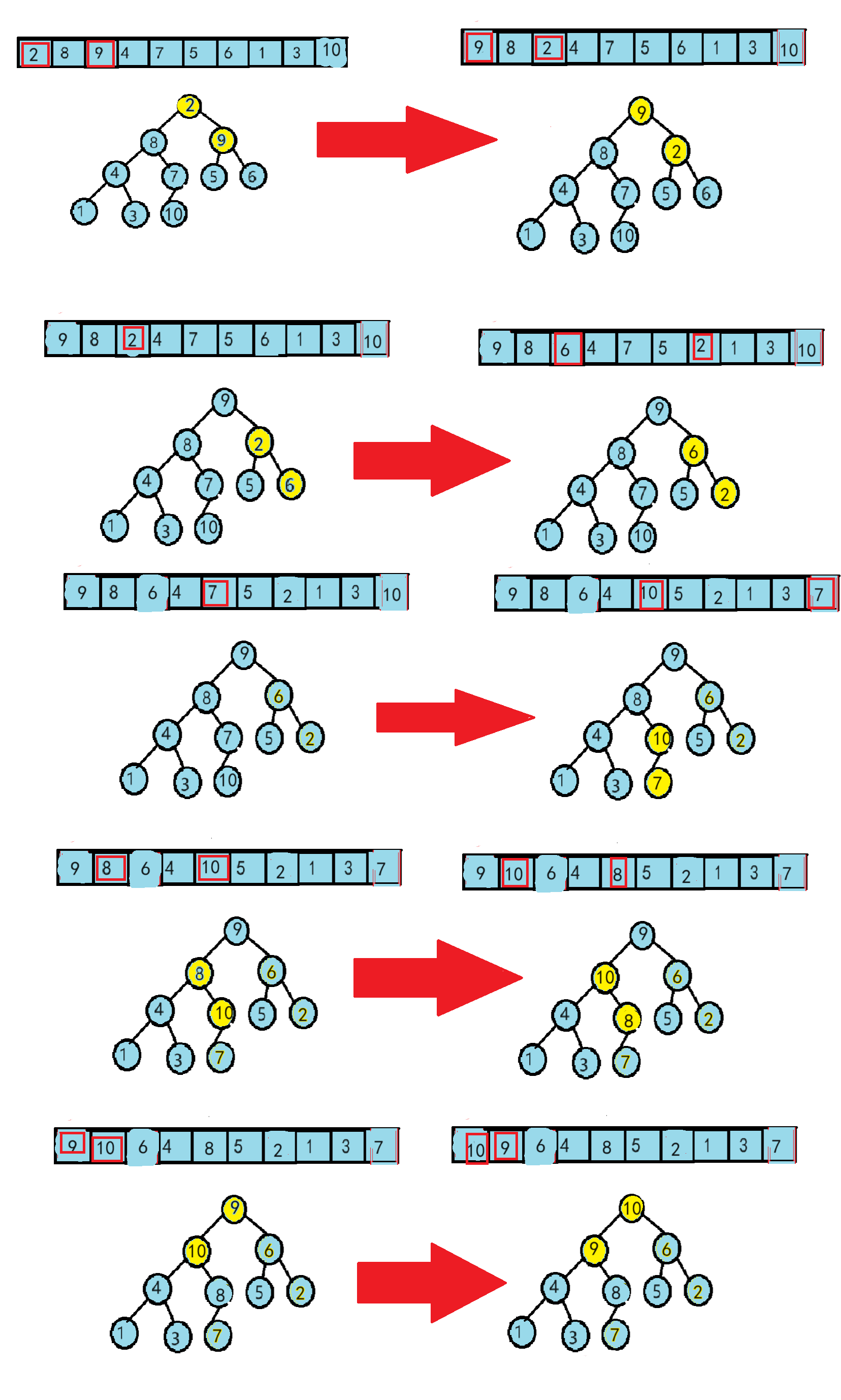
  假设有一个数组：arr[ ] = {2, 8, 9, 4, 7, 5, 6, 1, 3, 10}

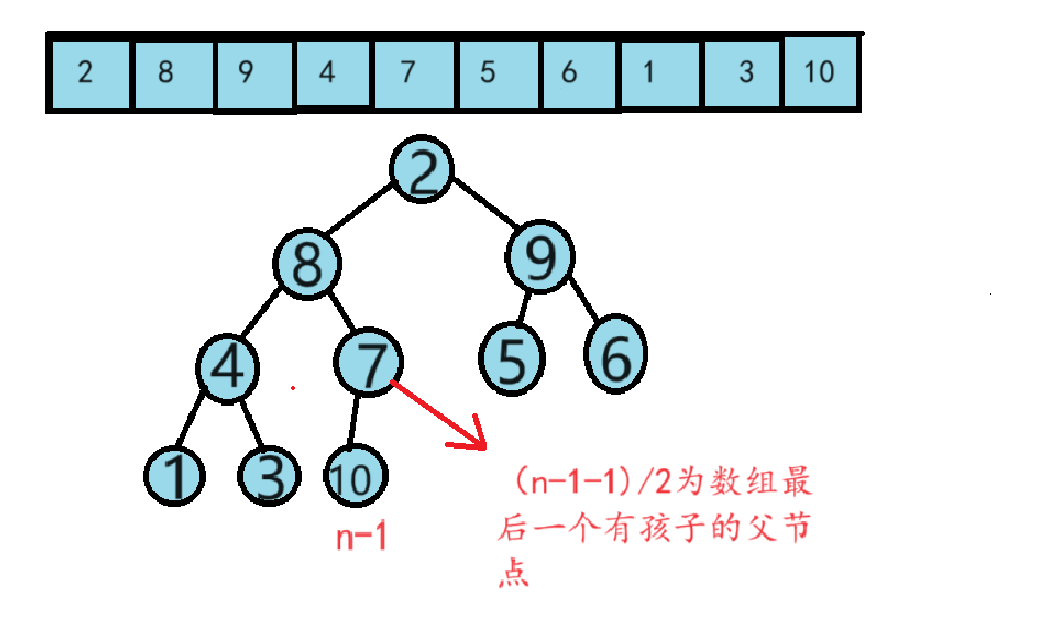
  接下来，根据代码对数组元素进行比较：从以数字7为父节点开始进行调整

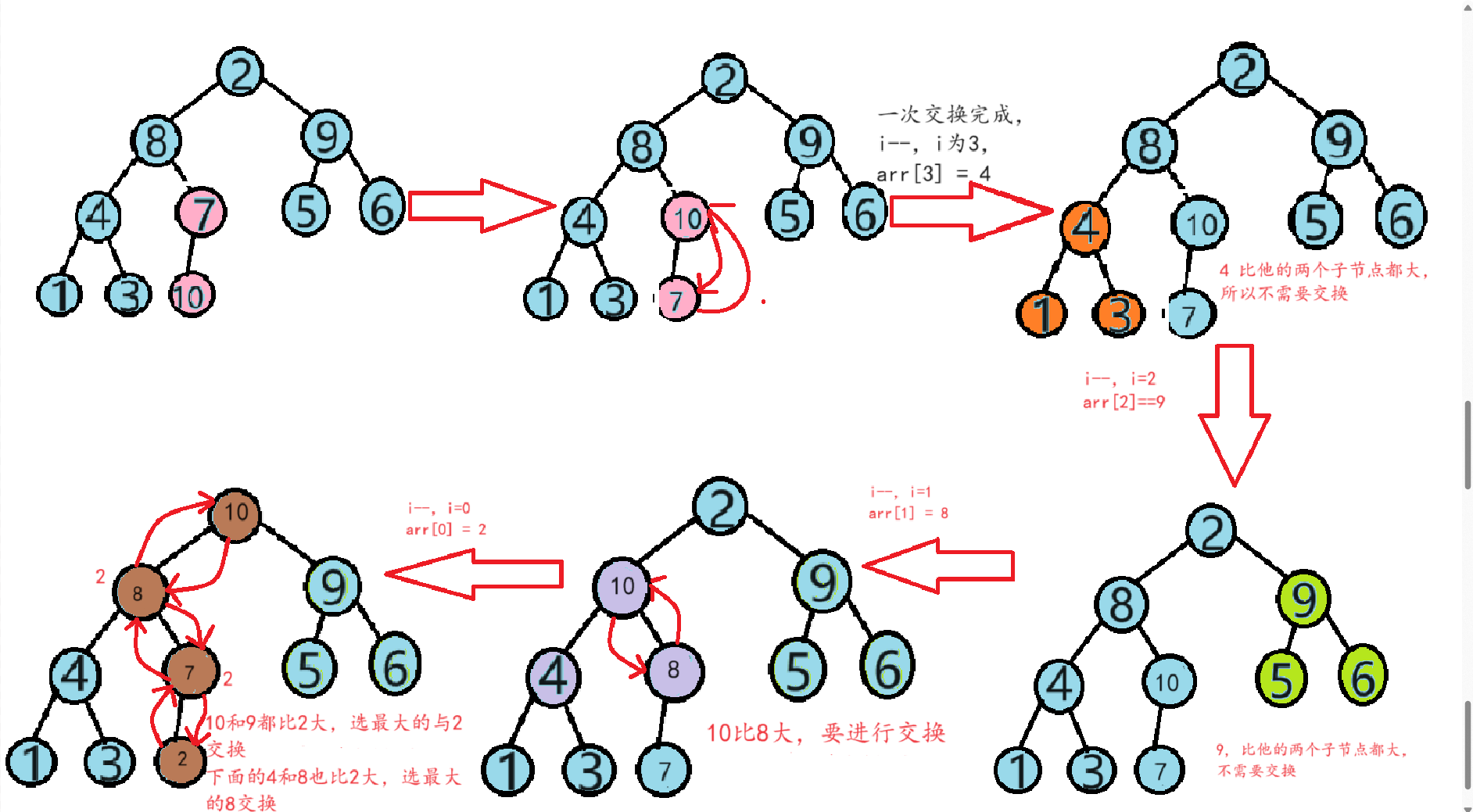
以上是向上调整建堆的全过程，最终得到数组arr[ ] = {10, 8, 9, 4, 7, 5, 6, 1, 3, 2}。

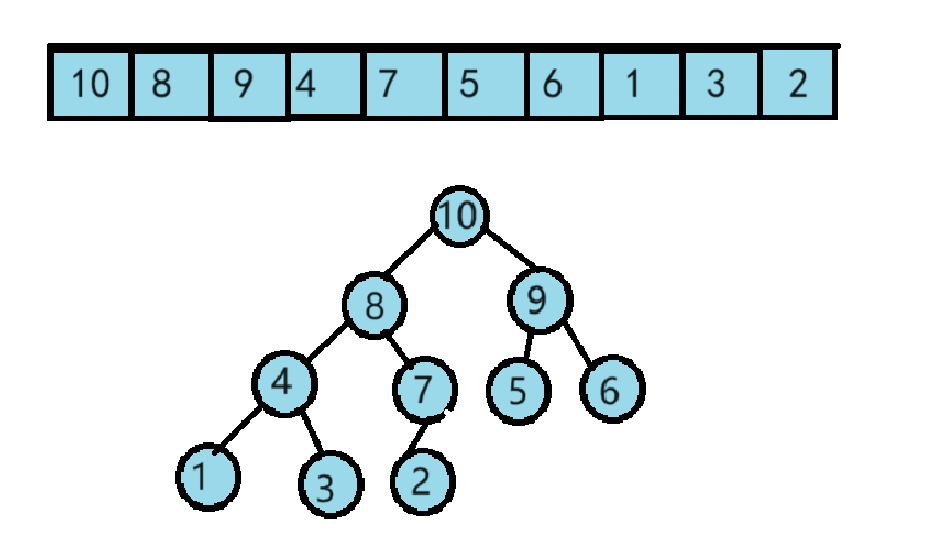
排序

  建完堆就该排序了

void HeapSort(int* arr, int n)
{//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}

  变量end代表数组最后一个元素下标，排序需要遍历数组，所以end也可做完while循环的判断条件。
  这里将arr[0]与arr[end]交换，再进行向下调整，遍历整个数组，结束后数组变为有序数组，堆排序也就完成了。


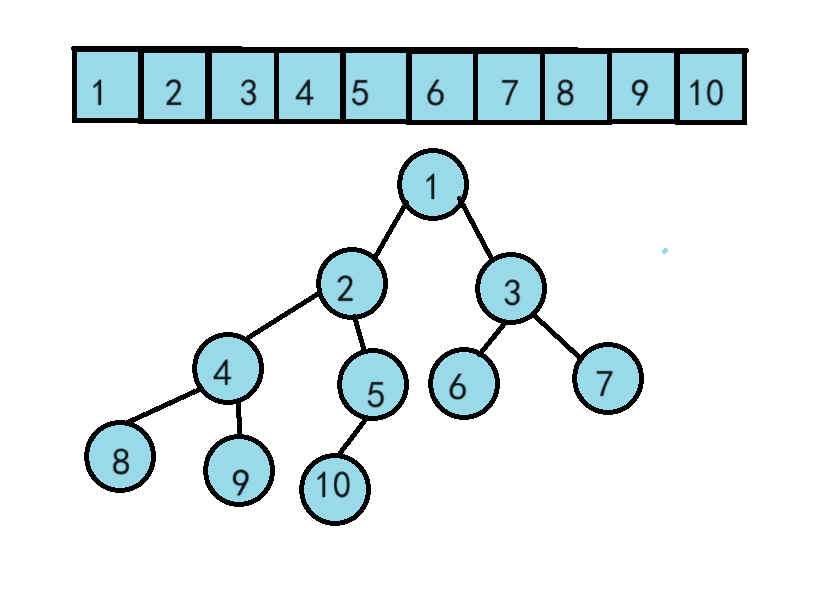
  首先，将2和10进行交换

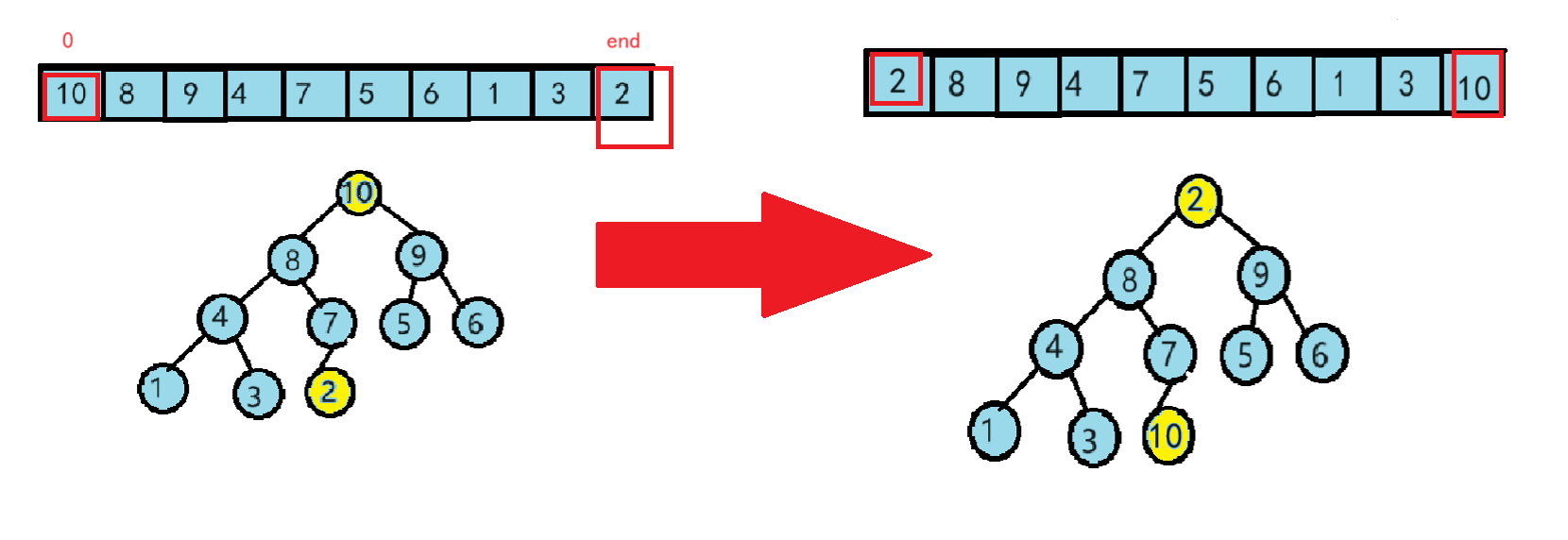
  从上向下依次进行比较，较大的数往下走，较小的数往上走。

以上是一次循环的过程，后面的循环同理，最后就会的到一组有序的数组。

  每一次循环结束后，end–， 继续将arr[0]与arr[end]交换，继续进行同样的排序。

四、 完整代码

//堆排序
//降序建小堆
//升序建大堆
void Swap(int* x, int* y)
{int ret = *x;*x = *y;*y = ret;
}void AdjustUp(int* arr, int child)
{int father = (child - 1) / 2;//while (child > 0)while(father >= 0){if (arr[father] < arr[child])//大堆  升序//if (arr[father] > arr[child])//小堆  降序{Swap(&arr[father], &arr[child]);child = father;father = (child - 1) / 2;}else{break;}}
}void AdjustDown(int* arr, int n, int father)
{//假设左大int child = 2 * father + 1;while (child < n){//找出最大的孩子//if (child + 1 < n && arr[child + 1] < arr[child])//小堆， 降序if (child + 1 < n && arr[child + 1] > arr[child])//大堆， 升序{child++;}//if (arr[father] > arr[child])//小堆， 降序if (arr[father] < arr[child])//大堆， 升序{Swap(&arr[father], &arr[child]);father = child;child = 2 * father + 1;}else{break;}}}void HeapSort(int* arr, int n)
{//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}//向上调整建堆/*for (int i = 1; i < n; i++){AdjustUp(arr, i);}*/int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
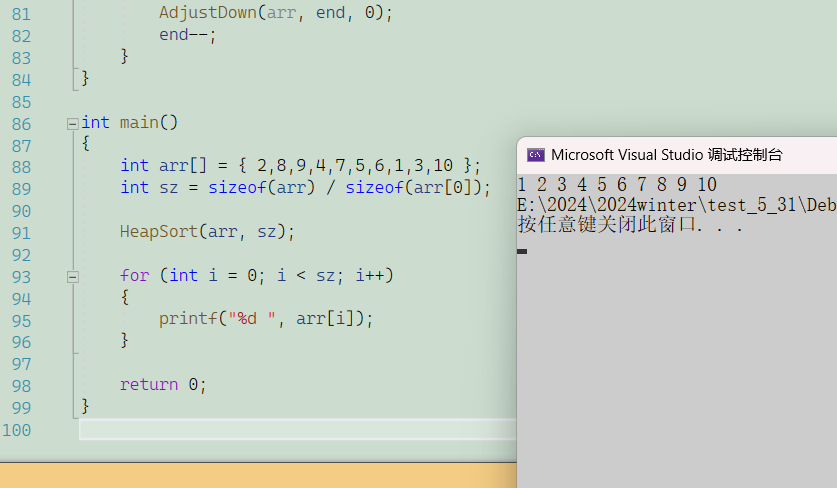
}int main()
{int arr[] = { 2,8,9,4,7,5,6,1,3,10 };int sz = sizeof(arr) / sizeof(arr[0]);HeapSort(arr, sz);for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}return 0;
}