题解：柠檬水找零(贪心算法)

1.题目

题目链接：LINK

2.题解

分情况讨论 + 贪心算法

• 当顾客为5元时，收下
• 当顾客为10元时，收下10元并找回5元
• 当顾客为20元时，收下20元并找回10+5元或者5+5+5元

这里仅20元时候找钱会有分歧，所以这里我们用贪心算法，即优先留下尽可能多的5元，尽快把10元扔出去。

原因：5元是“万金油”，既可以给10元找零，也可以给20元找零，但是10元就不能给10元找零。

3.参考代码

class Solution {
public:bool lemonadeChange(vector<int>& bills) {//哈希数组int arr[2] = {0};//0：5元 1：10元for(auto& money: bills){if(money == 5) arr[0]++;else if(money == 10) arr[1]++,arr[0]--;// 收钱 + 找钱else{//收钱arr[2]++;//找钱if(arr[1] >= 1 && arr[0] >= 1) arr[1]--,arr[0]--;else arr[0]-=3;} if(arr[0] < 0) return false;}return true;}
};

4.证明

证明思路：交换论证法
如果最优解和贪心解可以相互交换，即证明贪心解法有效。
注：最优解这里可以认为一定正确的解法。

因为在顾客给5元或者10元时候，找钱策略是唯一的，因而没有区别，我们这里只讨论顾客给20元的场景。

如果顾客给20元，
贪心算法：10 + 5元
最优解：5+5+5(可能，我们讨论最优解也为10 + 5的没意义)

如果这样，区别就在于一个10元的问题。
当这个10元在后面没有用，那么贪心解和最优解一致，因为这个10元没有用。
当这个10元在后面用到了，无非就是下面这种情况，可以看到无非贪心解和最优解顺序不一样而已。

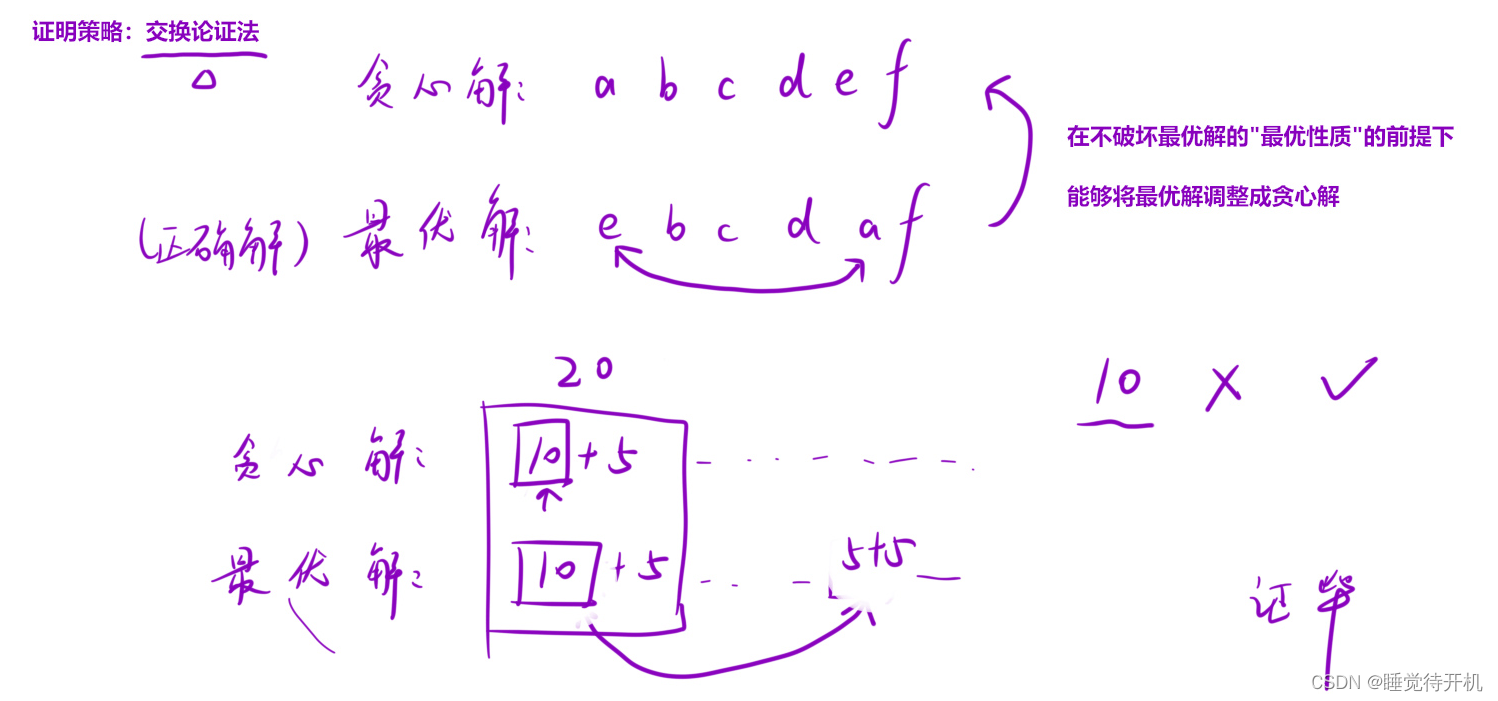
在某种程度上，我觉得贪心算法一定是正确解法的一种，所以这个题贪心算法是正确的。

5.总结

---

EOF