OpenCV学习基础图像操作（十六）：图像距离变换

基础原理

顾名思义，我们可以利用像素之间的距离作为对该像素的一种刻画，并将其运用到相应的计算之中。然而，在一幅图像之中，某种类型的像素并不是唯一的，因此我门常计算的是一类像素到另一类的最小距离，并且如何去定义和求解对应的像素也是可以根据问题去选择的。

朴素的来看，这是一个计算复杂度很高的运算，因为我们需要对两种类别中的像素进行两两遍历求得起距离才能找到最小距离，然而实际中我们会充分利用空间位置关系，以及采样的方法来加速这个算法过程。

下面参考Distance Transforms of Sampled Functions中所述，来简单地介绍一下整个算法的思路：

首先，我们从问题转换为数学表示，假设在坐标轴上， $G= 0,...,n-1$ ，有如下变换：

$D_f(p)=\underset{q\in \mathfrak{g}}{min}(d(p,q)+f(q))$

其中 $D_f$ 为从 $q$ 变换到 $p$ 的距离， $d(p,q)$ 为度量距离的方式， $q$ 为坐标中任意一点， $f(q)$ 表示点 $q$ 的集合

$f(q) =\begin{cases} 0 & \text{ if } q\epsilon P \\ \infty & \text{ othersize} \end{cases}$

最小值卷积

此处由于相似的形式，我们引入最小卷积，与正常的卷积一样最小卷积，遵守交换律与结合率。

$(f\bigotimes g)(p)=\underset{q}{min}(f(q)+g(p-q))$

上式中，我们假设在一维的轴上进行测量，那么将 $d(p,q)$ 替换为 $g(p-q)$ ，则距离变换就变为了 $fg$ 在 $p$ 处的卷积了。

式子的右半边是一个最优化问题，即调整 $q$ 寻找到最小值，那么将左半边的卷积也写为与右边相似的形式，即将卷积拆为一下形式：

${\delta}'(q)=b(q)+min(\delta (p)+a(p,q))$

${\delta}'(q)=b(q)+D_\delta (q)$

经过这样的变换后，可以看到式子迭代已经将另一个点排除在外了，即所求解的是一个全局的值。但是由于空间中点与点是有一定顺序的，我们可以利用动态规划等手段，优化这个线性的求解过程，最终将算法复杂度由 $O(n^2)$ 优化到 $O(n)$ 。

一维上的变换

结合实际例子来看一下，假设在数轴上使用欧式距离进行距离变换：

$D_f(p)=\underset{q\in \mathfrak{g}}{min}((p-q)^2+f(q))$

形象的可视化下，每一个可能的点 $p$ 的距离变换后的值为

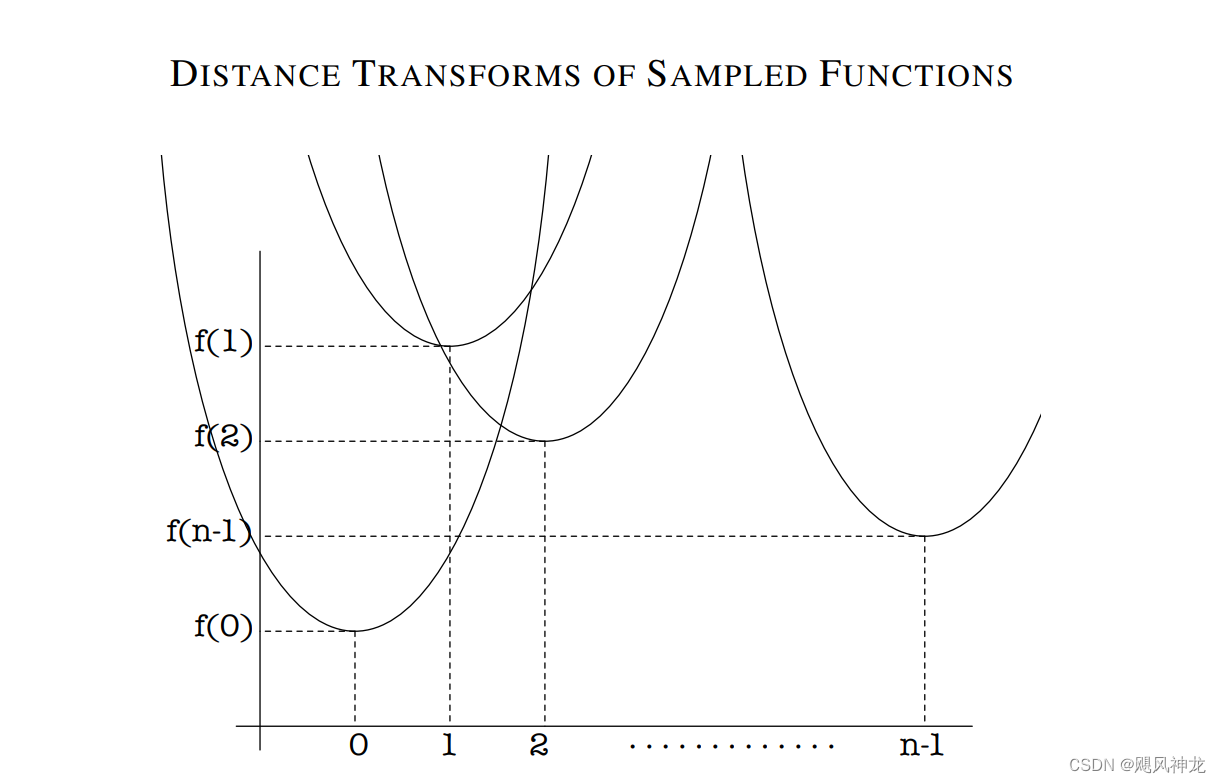
我们需要找到就是在各个点距离变换后，在点 $r$ 与 $q$ 中的最小值处 $s$ ，以此作为采样点，进行实际的剧离运算，s的计算可表示为：

$s=\frac{(f(r)+r^2)-(f(q)+q^2)}{2r-2q}$

我们从左往右，依次记录每个抛物线交点的下包络并存到 $v[i]$ 中，下包络线的第 i 条抛物线低于其他抛物线的范围由 $z[i]$ 和 $z[i+1]$ 给出， $k$ 表示第几根抛物线。则推理计算过程可以写为：

可视化其中s的更新过程为下图：

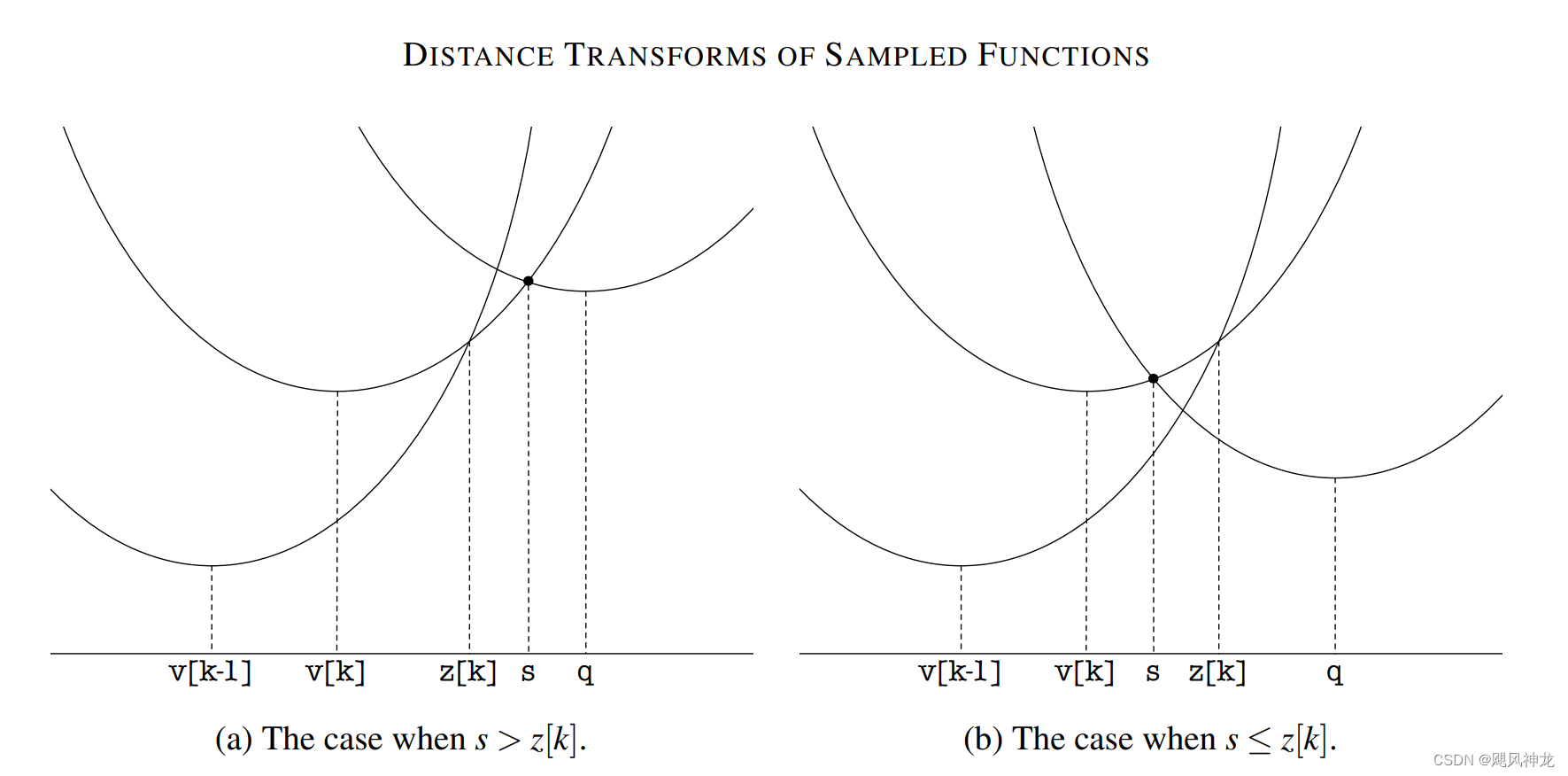
API介绍


void cv::distanceTransform	(	InputArray 	src,  //输入的原图
OutputArray 	dst,                              //输出的距离变换map
OutputArray 	labels,                           //输出的标签map
int 	distanceType,                             //距离的类型
int 	maskSize,                                 //距离变换掩码矩阵的大小
int 	labelType = DIST_LABEL_CCOMP              //类别的类型
)

这意味着，对于一个像素，该函数会找到到最接近的零像素的最短路径，该路径由基本位移组成：水平、垂直、对角线或骑士移动（最新的可用于5×5面具）。总距离计算为这些基本距离的总和。由于距离函数应该是对称的，因此所有水平和垂直移动必须具有相同的成本（表示为），所有对角线移动必须具有相同的成本（表示为），并且所有骑士的移动必须具有相同的成本（表示为）。对于DIST_C和DIST_L1类型，距离是精确计算的，而对于DIST_L2（欧几里得距离），距离只能通过相对误差（abc5×5mask 提供更准确的结果）。对于、和，OpenCV 使用原始论文中建议的值：abc

DIST_L1：a = 1, b = 2
DIST_L2：
3 x 3:a=0.955, b=1.3693
5 x 5:a=1, b=1.4, c=2.1969
DIST_C：a = 1, b = 1

通常，对于快速、粗略的距离估计DIST_L2，一个3×3使用面具。为了更准确地估计距离DIST_L2，一个5×5掩码或使用精确算法。请注意，精确算法和近似算法在像素数上都是线性的。

该函数的此变体不仅计算每个像素的最小距离(x，y)还可以标识由零像素（labelType==DIST_LABEL_CCOMP）或最接近的零像素（labelType==DIST_LABEL_PIXEL）组成的最近连接组件。分量/像素的索引存储在中。当 labelType==DIST_LABEL_CCOMP 时，该函数会自动在输入图像中查找零像素的连接组件，并用不同的标签标记它们。当 labelType==DIST_LABEL_PIXEL 时，该函数会扫描输入图像，并使用不同的标签标记所有零像素。labels(x, y)

在这种模式下，复杂度仍然是线性的。也就是说，该函数提供了一种非常快速的方法来计算二进制图像的 Voronoi 图。目前，第二个变体只能使用近似距离变换算法，即尚不支持 maskSize=DIST_MASK_PRECISE。

简单使用一下，来找一下毛笔字的骨骼，自制一个描红本

import cv2
import matplotlib.pyplot as plt
def main():#读取图像img = cv2.imread("D:\code\src\code\zhen.jpg",cv2.IMREAD_GRAYSCALE)#二值化分割thresh,binary = cv2.threshold(img,50,255,cv2.THRESH_BINARY_INV)#利用距离变换找到骨骼脉络dist = cv2.distanceTransform(binary,cv2.DIST_L2,3)#利用自适应二值化保存脉络上局部最大值sk = cv2.adaptiveThreshold(dist.astype("uint8"),255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY_INV,9,0)plt.subplot(411),plt.imshow(img,cmap='gray'),plt.title('Source Image'), plt.xticks([]), plt.yticks([])plt.subplot(412),plt.imshow(binary,cmap='gray'),plt.title('Binary Image'), plt.xticks([]), plt.yticks([])plt.subplot(413),plt.imshow(dist),plt.title('Dist Map'), plt.xticks([]), plt.yticks([])plt.subplot(414),plt.imshow(sk,cmap='gray'),plt.title('Skelet Image'), plt.xticks([]), plt.yticks([])plt.show()if __name__ == "__main__":main()