本次我们通过连通块中点的数量来加深我们对并查集的基本操作和原理,并且知道如何在并查集中添加附属信息。
目录
前言☀
一、连通块中点的数量☀
二、算法思路☀
1.无向图🌙
2.在a b之间连一条边,a b可能相等🌙
3.询问a和b是否在一个连通块中,a和b可能相等🌙
4.询问点所在连通块中点的数量🌙
三、代码如下☀
1.代码如下:🌙
2.读入数据🌙
3.代码运行结果🌙
4.代码样例解释🌙
总结☀
前言☀
本次我们通过连通块中点的数量来加深我们对并查集的基本操作和原理,并且知道如何在并查集中添加附属信息。
提示:以下是本篇文章正文内容,下面案例可供参考
一、连通块中点的数量☀
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b可能相等;Q1 a b,询问点 a 和点 b是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤100000
二、算法思路☀
1.无向图🌙
图1.1无向图示例
我们有各种各样的点,然后通过一条边进行连接,且这条边没有方向,例如A与B之间有条边,那么A可以到达B,B也可以到达A;图1.1就是一个无向图。
我们还是引入一个一维整型数组p来存储各个结点的父结点的编号,p数组的索引就表示哪个结点。在这道题中我们还需要引入一个一维整型数组size,用来记录每个集合内结点的个数即我们题上说的连通块内点的个数;规定只有根节点的size数组内的值是有效的。
for(int i = 1;i <= n;i++){p[i] = i;size[i] = 1;}这道题跟并查集类似,我们还是需要一个find方法来找到结点x所在集合的根节点的编号。
public static int find(int x){if(p[x] == x){return x;}return p[x] = find(p[x]);}对于上述find方法代码如果不太理解的,可以去看我之前写的合并集合的博客(https://blog.csdn.net/m0_63267251/article/details/139294176)里面,里面有详细的解释。
2.在a b之间连一条边,a b可能相等🌙
图2.1添加边样例图
在这道题中我们往两个点中添加边,a和b如果相等,那么就是一个点自连如图2.1右边所示。还有可能两个点之间已经右边,然后有重复添加了一条边。
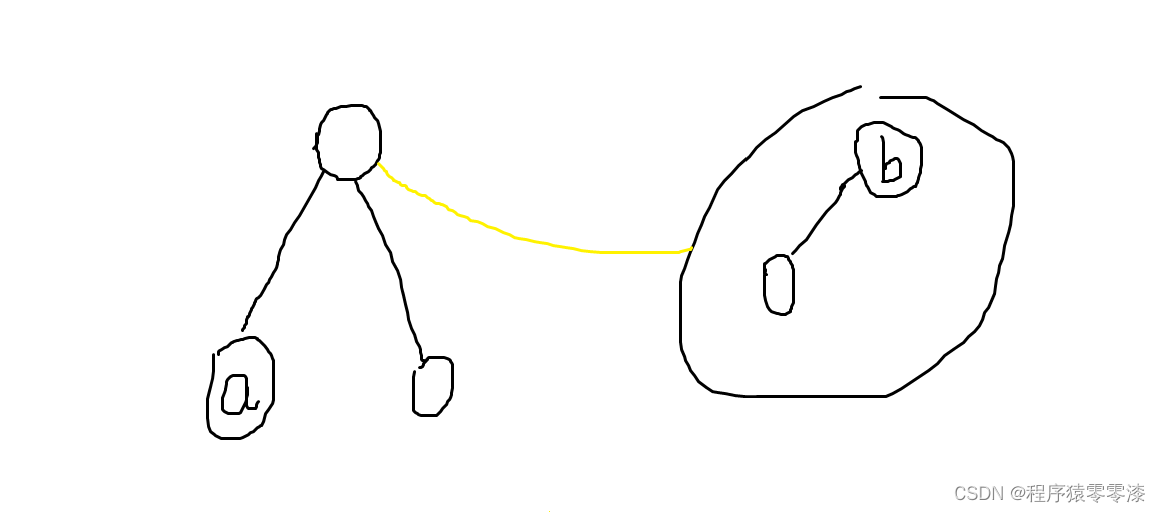
图2.2size数组维护
我们要添加边,其实就相当于我们把两个集合给合并了一样,例如我们在a和b两个点添加一条边,其实就是将a和b所在的两个集合合并,那么我们只需要找到b所在集合的根节点,然后让b所在集合根节点的父结点变成a所在集合的根节点就完成了合并操作即p[find(b)] = find(a);

我们还有一个很重要的操作需要维护size数组里面的值,因为我们相当于把b所在集合放到了a所在集合的下面,那么我们只需要将所在a结点集合结点个数加上b所在集合对应的结点个数即可,我们规定了只有根节点的size值是有效的,那么我们只需要 size[find(a)] += size[find(b)]就可完成上述操作。
当然如果a结点和b结点在同一个集合的话,我们就不需要进行size数组的维护了,中间加一个判断。‘
if(cmd.equals("C")){a = sc.nextInt();b = sc.nextInt();//当a和b已经在一个集中当中,就不需要再改变对应根节点的size值了,不在进行后续size 数组值的更新和根节点值得改变if(find(a) == find(b)){continue;}size[find(a)] += size[find(b)];p[find(b)] = find(a);
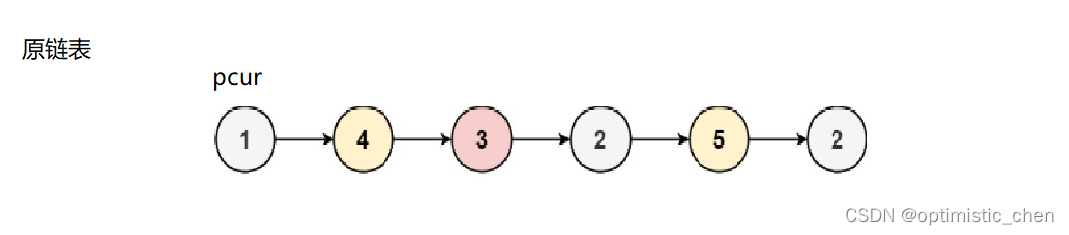
3.询问a和b是否在一个连通块中,a和b可能相等🌙
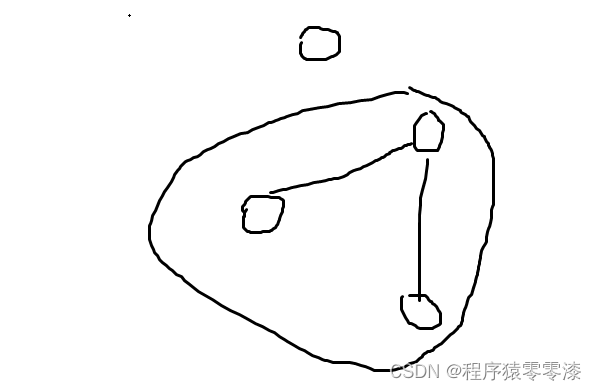
图3.1连通块示例
判断两个点是不是在一个连通图中,即a可以到达b,b也可以到达a,就说明两个点是在一个连通图中。如上图3.1中圈起来的就是一个连通图。
我们只需要判断一下结点a所在集合的根节点的值和结点b所在集合的根节点的值是否相等就可判断出是否在同一个连通块中。
find(a) == find(b) ? "Yes":"No"
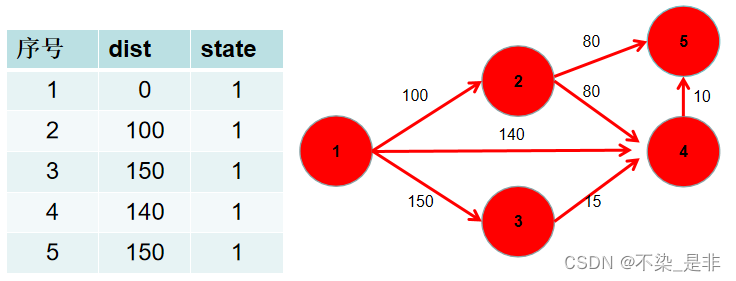
4.询问点所在连通块中点的数量🌙
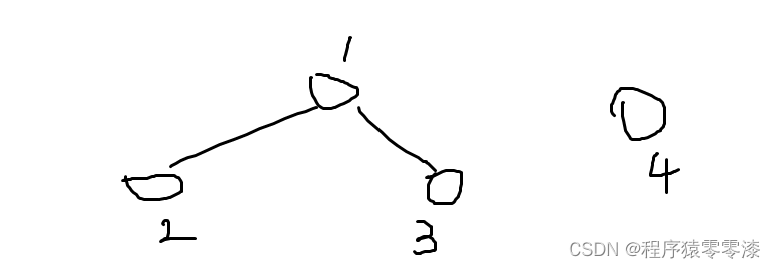
图4.1示例图
如图4.1所示我们可以看到点1的连通块中有3个点,点4所在的连通块中的点的数量是1。
这里我们只需要返回对应点所在集合的根节点的size数组值就是集合所在连通块中点的个数
size[find(a)]三、代码如下☀
1.代码如下:🌙
import java.util.*;
import java.io.*;
public class Main {static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int N = 100010;static int[] p = new int[N];//用来记录对应结点的集合内所有点的个数static int[] size = new int[N];public static void main(String[] args)throws Exception {Scanner sc = new Scanner(br);int n = sc.nextInt();for(int i = 1;i <= n;i++){p[i] = i;size[i] = 1;}int m = sc.nextInt();while (m-- > 0){String cmd = sc.next();int a,b;if(cmd.equals("C")){a = sc.nextInt();b = sc.nextInt();//当a和b已经在一个集中当中,就不需要再改变对应根节点的size值了if(find(a) == find(b)){continue;}size[find(a)] += size[find(b)];p[find(b)] = find(a);} else if (cmd.equals("Q1")) {a = sc.nextInt();b = sc.nextInt();pw.println(find(a) == find(b) ? "Yes":"No");} else if (cmd.equals("Q2")) {a = sc.nextInt();pw.println(size[find(a)]);}}pw.flush();}public static int find(int x){if(p[x] == x){return x;}return p[x] = find(p[x]);}}
2.读入数据🌙
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 53.代码运行结果🌙
Yes
2
34.代码样例解释🌙
C 1 2 后1和2在同一个集合;Q1 1 2查询1和2是否在同一个集合打印Yes;Q2 1查询1所在集合点的个数为2;C 2 5 将2和5想连,那么1 2 5在同一个集合;Q2 5查询5所在集合点的个数为3。

总结☀
上述通过连通块中点的数量这道题又训练了一遍并查集的基本操作,本质和并查集的代码并无差别,只是我们在并查集的操作过程中可以加入一些维护信息。