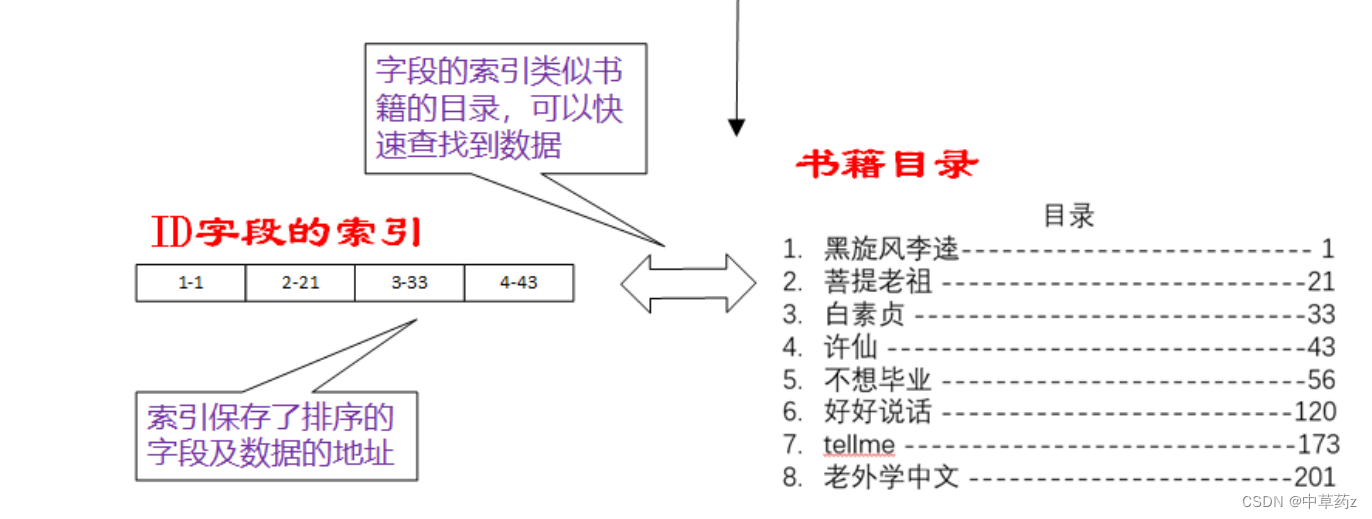
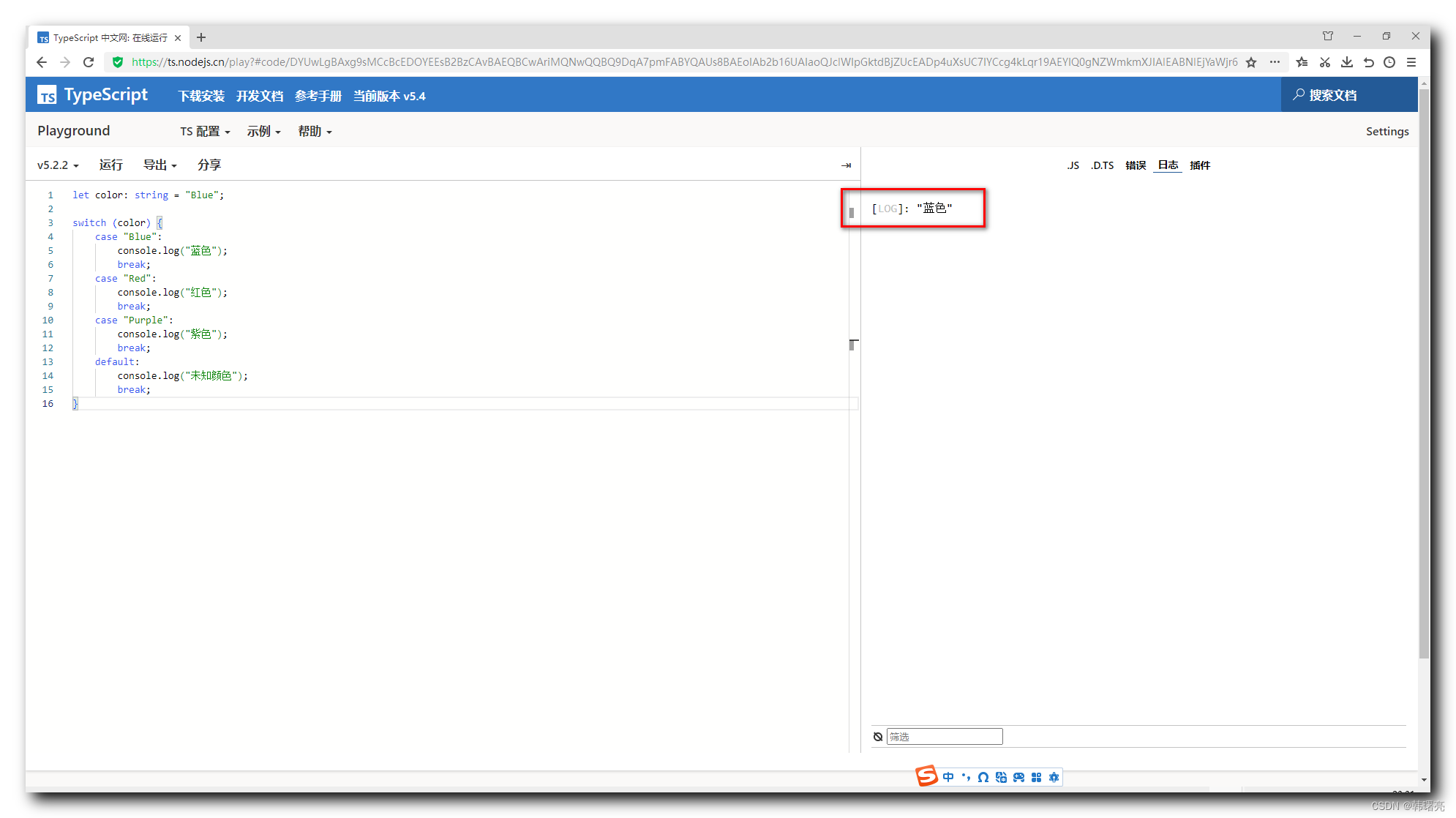
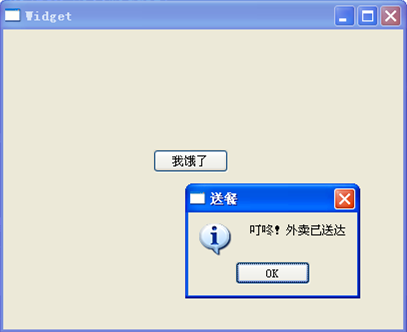
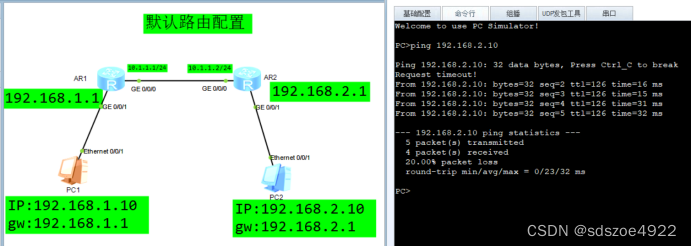
在上一篇博文用贪心算法计算十进制数转二进制数(整数部分)-CSDN博客中,小编介绍了用贪心算法进行十进制整数转化为二进制数的操作步骤,那么有朋友问我,那十进制小数转二进制,可以用贪心算法来计算吗?我研究了一下,发现也是可以用的,下边介绍一下操作步骤。
目录
一、乘2正向取整法
二、十进制小数转化为二进制小数的数学原理
三、贪心算法
1、贪心算法简介
2、操作步骤
3、结论
一、乘2正向取整法
在介绍贪心算法之前,还是先介绍一下常用的计算方法,就是“乘2取整”法。
这种方法就是把十进制的小数部分乘2,并记录得到的积的整数部分,把积的整数部分减掉,再把积的小数部分进行乘2,并记录得到的积的整数部分,依次乘2取整,直到乘2后得到的积为1,也就是整数部分为1,小数部分为0时,转化完成。转化完成后,从上往下(正向)依次把整数部分排列起来,就是转化后的二进制小数。

注意,并不是所有的十进制小数都能精确地转化为二进制小数。如果出现乘2后的积一直不为1的情况时,此十进制小数就不能精确转化为二进制小数,只能无限接近。
例如,十进制小数0.15就无法精确地转换为二进制,转化的结果为0.001001100110011……循环不尽,无法得到精确转化值。
二、十进制小数转化为二进制小数的数学原理
通过观察图1,可以看出:
(1)
一般的表达式为:
(2)
十进制小数转化为二进制小数的过程就是把系数从
到
(从最高位到最低位)的排列。
在(1)式中,,所以
。
如果把(1)式中的系数 的项去掉,那么有
(3)
也就是把十进制小数转换为二进制小数的过程,实际上就是把十进制小数转换为若干个以2为底的幂运算之和,那么一般表达式为:
(4)
在(3)式中,。也就是在十进制小数0.6825转换为二进制小数后,数位序号为1,3,4的项系数为1,其他项系数都为0(数位序号从左向右依次增1,最低位序号为1),如表1所示,表格中橙色项系数为1,白色项系数为0。
| 位序号 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 位权重 | 1/2 | 1/4 | 1/8 | 1/16 |
| 项系数 | 1 | 0 | 1 | 1 |
| 二进制数 | 1 | 0 | 1 | 1 |
三、贪心算法
那么如何快速计算出(4)式的呢?与十进制整数转化二进制数类似,也可以用贪心算法进行计算。
1、贪心算法简介
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
2、操作步骤
假设十进制数为,根据公式(4),用贪心算法思维进行十进制小数转二进制小数计算的步骤为:
(1)先找出中最大的那一项
,并记录
;
(2)把最大项的值从中减掉:
(3)跳转到步骤(1)循环计算,直到或
给定极小值,计算结束。
为了人工计算更直观,我们通常把写为小数形式0.5,0.25,0.125,0.0625,0.03125。
因此(1)式右边的指数形式转化为小数形式
(5)
同样,可以把(3)式改写为:
(6)
下边以十进制小数转化为二进制小数为例,介绍贪心算法的计算步骤:
(1)找出0.6875中最大的项为0.5,也就是,记录
;
(2);
(3)找出0.1875中最大的项为0.125,也就是,记录
;
(4);
(5)找出0.0625中最大的项为0.0625,也就是,记录
;
(6),计算结束;
计算的结果为:0.6875=0.5+0.125+0.0625=
二进制小数位序号为1,3,4的项为1,其他位序号的项为0,计算结果为。
3、结论
对比乘2取整法和贪心法,可以发现,对于可以转化为精确二进制小数的情况来说,贪心算法计算量少,准确率较高,不容易算错,也更直观,更好理解和记忆,但是需要我们事先记住一些常用的的值,这样才有助于我们更快找出最大项。表2为
的
的值。
| 值 | 0.5 | 0.25 | 0.125 | 0.0625 | 0.03125 |
(本文结束)