24.6.2（动态开点线段树）

星期一：

cf edu round 36 E cf传送门

题意：1到n天初始全为工作日，有两种操作，将 l-r 区间变为工作日/休息日，每次操作后询问剩余总工作日有多少

思路：线段树维护，有几种做法，这里用的是动态开点线段树，mle和re了很多次，因为这题的数据范围不用开 ll，结构体里用 int就不会爆内存了

代码如下：

const int N=3e5+10,M=210;
ll n;
struct d_Seg_Tree{
#define lc(x) t[x].ch[0]
#define rc(x) t[x].ch[1]struct nod{int ch[2];            //左右儿子节点的编号int sum,tag;}t[N*55];int root;ll tot;int ql,qr,qop;void pushup(int p){t[p].sum=t[lc(p)].sum+t[rc(p)].sum;}void pushdn(int p,int l,int r){if(!t[p].tag) return ;if(!lc(p)) lc(p)=++tot;if(!rc(p)) rc(p)=++tot;int mid=l+r>>1;if(t[p].tag==1){t[lc(p)].sum=mid-l+1;t[rc(p)].sum=r-mid;t[lc(p)].tag=t[rc(p)].tag=t[p].tag;}if(t[p].tag==-1){t[lc(p)].sum=t[rc(p)].sum=0;t[lc(p)].tag=t[rc(p)].tag=t[p].tag;}t[p].tag=0;}void update(int &p,int l,int r){if(!p) p=++tot;                          //新建节点if(ql<=l && qr>=r){if(qop==1){t[p].sum=r-l+1;t[p].tag=1;}else{t[p].sum=0;t[p].tag=-1;}return ;}int mid=l+r>>1;pushdn(p,l,r);if(ql<=mid) update(lc(p),l,mid);if(qr>mid) update(rc(p),mid+1,r);pushup(p);}void updt(int l,int r,int op){ql=l,qr=r;qop=op;update(root,1,n);}
}tr;
void solve(){int q; cin >> n >> q;while(q--){int op;int x1,x2; cin >> x1 >> x2 >> op;tr.updt(x1,x2,op);cout << n-tr.t[tr.root].sum << "\n";}
}

19届东南校赛 B cf传送门

思路：这里用的动态开点线段树，折磨了我一个晚上

注意二分配线段树 O(log^2 * q)的复杂度会T，但结果一直显示的re，所以一直以为是空间没开够，但N*207已经是极限了（实测，一度怀疑动态开点线段树的空间复杂度到底怎么算（现在也还没明白），后来试了下线段树上二分，就过了。。

代码如下：

const int N=3e5+10,M=210;
ll n;
const ll MAXN=2e18+10;
struct d_Seg_Tree{
#define lc(x) t[x].ch[0]
#define rc(x) t[x].ch[1]struct nod{ll ch[2];ll sum;int tag;}t[N*152];                  //最少也需要N*152(实测)ll root;ll tot;ll ql,qr,qop;void pushup(ll p){t[p].sum=t[lc(p)].sum+t[rc(p)].sum;}void pushdn(ll p,ll l,ll r){if(!t[p].tag) return ;if(!lc(p)) lc(p)=++tot;if(!rc(p)) rc(p)=++tot;ll mid=l+r>>1;if(t[p].tag==1){t[lc(p)].sum=mid-l+1;t[rc(p)].sum=r-mid;t[lc(p)].tag=t[rc(p)].tag=t[p].tag;}if(t[p].tag==-1){t[lc(p)].sum=t[rc(p)].sum=0;t[lc(p)].tag=t[rc(p)].tag=t[p].tag;}t[p].tag=0;}void update(ll &p,ll l,ll r){if(!p) p=++tot;if(ql<=l && qr>=r){if(qop==1){t[p].sum=r-l+1;t[p].tag=1;}else{t[p].sum=0;t[p].tag=-1;}return ;}ll mid=l+r>>1;pushdn(p,l,r);if(ql<=mid) update(lc(p),l,mid);if(qr>mid) update(rc(p),mid+1,r);pushup(p);}ll query(ll p,ll l,ll r,ll v){
//		if(l==r) return l;if(!p || !t[p].sum) return l+v-1;  //全0,可直接算出下标ll mid=l+r>>1;ll lenl=mid-l+1;ll numl=lenl-t[lc(p)].sum;                 //左儿子区间0的数量if(numl>=v) return query(lc(p),l,mid,v);else return query(rc(p),mid+1,r,v-numl);}void updt(ll l,ll r,char op){ql=l,qr=r;if(op=='+') qop=1;else if(op=='-') qop=0;update(root,1,MAXN);}
}tr;
void solve(){int q; cin >> q;while(q--){char op; cin >> op;if(op!='?'){ll x1,x2; cin >> x1 >> x2;x1++,x2++;tr.updt(x1,x2,op);}else{ll k; cin >> k;
//			ll l=1,r=MAXN,res=0;                  //每次询问log^2的复杂度,会T
//			while(l<=r){
//				ll mid=l+r>>1;
//				ll sum0=mid-tr.ask_sum(1,mid);
//				if(sum0<k) l=mid+1;
//				else res=mid,r=mid-1;
//			}
//			cout << res-1 << "\n";cout << tr.query(tr.root,1,MAXN,k)-1 << "\n";     //单log的复杂度}}
}

星期二：

补23广东 F cf传送门

思路：动态开点线段树，对每个颜色开一颗树，因为是动态开点，空间复杂度可接受

对于每次询问，二分套线段树找出左右边界，因为 k的大小有限制，可对 k的每个颜色单独查询，然后判断合法颜色数量是否等于区间长度，权值和可以用常数小的树状数组计算

注意线段树的细节不要写错，写漏（自省

单log的写法目前不会

代码如下：

const int N=1e5+10,M=210;
ll n;
ll t[N],v[N];
int c[N];
vector<int>co;
int lowbit(int x){return x&-x;}
void add(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) t[i]+=v;
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
struct d_Seg_Tree{
#define lc(p) t[p].ch[0]
#define rc(p) t[p].ch[1]struct nod{int ch[2];int sum;}t[N*40];int root[N];                     //每种颜色的根节点编号ll tot;int ql,qr,qv;void pushup(int p){t[p].sum=t[lc(p)].sum+t[rc(p)].sum;}void update(int &p,int l,int r){if(!p) p=++tot;if(ql<=l && qr>=r){t[p].sum+=qv;return ;}int mid=l+r>>1;if(ql<=mid) update(lc(p),l,mid);if(qr>mid) update(rc(p),mid+1,r);pushup(p);}int query(int p,int l,int r){if(!p) return 0;if(ql<=l && qr>=r) return t[p].sum;int mid=l+r>>1;int res=0;if(ql<=mid) res+=query(lc(p),l,mid);if(qr>mid) res+=query(rc(p),mid+1,r);return res;}void updt(int c,int l,int r,int v){ql=l,qr=r;qv=v;update(root[c],1,n);}int ask(int c,int l,int r){ql=l,qr=r;return query(root[c],1,n);}bool check(int l,int r){int sum=0;for(auto i:co) sum+=ask(i,l,r);return sum==r-l+1;}
}tr;
void clr(){for(int i=1;i<=tr.tot;i++) tr.t[i].sum=tr.t[i].ch[0]=tr.t[i].ch[1]=0;tr.tot=0;for(int i=1;i<=n;i++) tr.root[i]=t[i]=0;
}
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++){cin >> c[i];tr.updt(c[i],i,i,1);}for(int i=1;i<=n;i++){cin >> v[i];add(i,v[i]);}while(q--){int op; cin >> op;if(op!=3){int p,x; cin >> p >> x;if(op==1){tr.updt(c[p],p,p,-1);tr.updt(x,p,p,1);c[p]=x;}else add(p,x-v[p]),v[p]=x;}else{int x,k; cin >> x >> k;co.clear();for(int i=1;i<=k;i++){int a; cin >> a;co.push_back(a);        //存下合法颜色}int l=1,r=x,p1=0,p2=0;while(l<=r){                   //二分找左边界int mid=l+r>>1;if(tr.check(mid,x)) p1=mid,r=mid-1;else l=mid+1;}l=x,r=n;while(l<=r){                   //二分找右边界int mid=l+r>>1;if(tr.check(x,mid)) p2=mid,l=mid+1;else r=mid-1;}cout << ask(p2)-ask(p1-1) << "\n";}}clr(); //记得清空
}

刷刷马蹄疾 mtj传送门

思路：很典的数论题，但被拿下了，但其实二分也能过（二分的码就不贴了

吃糖一定会产生 k张糖纸，且最后手上至少还剩一张，能换的糖即为 (k-1)/p，k-(k-1)/p即为答案（什么数学大手子

代码如下：

void solve(){ll p,k; cin >> p >> k;if(k==0){cout << "0\n"; return ;}cout << k-(k-1)/p << "\n";
}

星期三：

23百度之星切蛋糕 mtj传送门

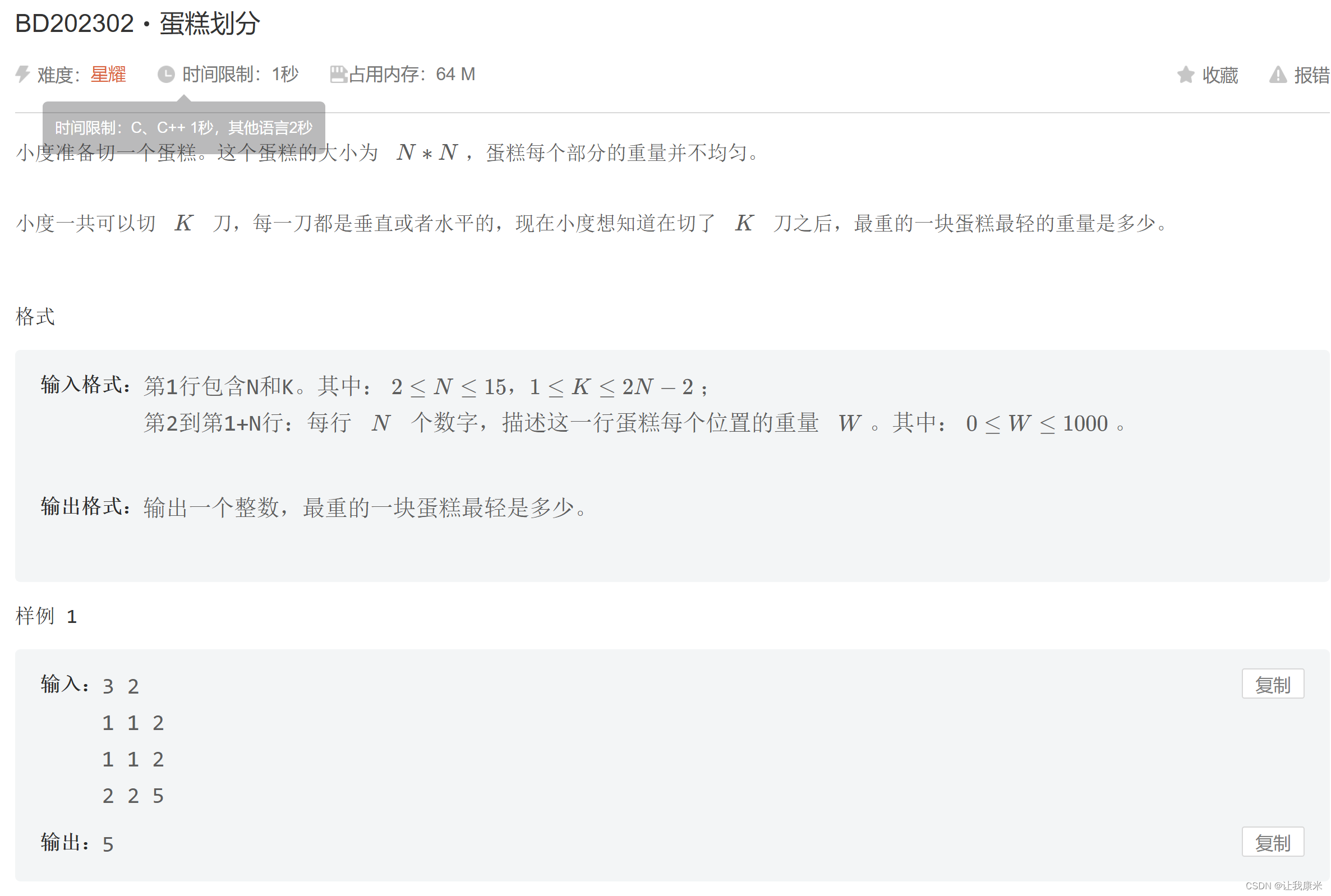
思路：说下歪解是怎么通过优化ac的

原本的思路是枚举竖切的状态，再对每次不同的竖切进行二分找到最优答案，但会超时

于是加入了朴素优化，开个countdown变量记录运行次数，在即将超时前退出，但这样程序可能在退出前没有得到正解。开始试了下正着和反着枚举状态，都有wa的点，最后改成先从后往前枚举到一半，再从前往后枚举到一半，成功冲过所有样例

代码如下：

const int N=2e6+10,M=210;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;
ll n;
int k;
int w[1010][1010];
void solve(){int countdn=1.6e7;            //运行倒计时cin >> n >> k;int mi=0,ma=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin >> w[i][j];mi=max(w[i][j],mi);ma+=w[i][j];}}int ans=1e9;int hf=((1<<n-1)-1)/2;                      //状态的中间值for(int mask=(1<<n-1)-1;mask>=hf;mask--){              //枚举后一半状态if(__builtin_popcount(mask)>k) continue;int lef=k-__builtin_popcount(mask);if(lef>=n) continue;vector<vector<int>>ve(22,vector<int>(22,0));for(int i=1;i<=n;i++){int idx=1;for(int j=1;j<=n;j++){ve[idx][i]+=w[i][j];if((mask>>j-1)&1) idx++;}}int l=mi,r=ma,res=1e9;while(l<=r){int mid=l+r>>1;bool if1=1;int tlef=lef;unordered_map<int,int>mp;int idx=__builtin_popcount(mask)+1;for(int j=1;j<=n;j++){for(int i=1;i<=idx;i++){countdn--;if(!countdn){cout << ans << "\n"; return ;}    //快超时了就退出mp[i]+=ve[i][j];if(ve[i][j]>mid){if1=0; break;}if(mp[i]>mid && !tlef){if1=0; break;}if(mp[i]>mid && tlef){tlef--;for(int y=1;y<=idx;y++){mp[y]=ve[y][j];if(mp[y]>mid){if1=0; break;}}break;}}if(!if1) break;}if(if1) res=mid,r=mid-1;else l=mid+1;}ans=min(res,ans);}for(int mask=0;mask<hf;mask++){                       //枚举前一半状态if(__builtin_popcount(mask)>k) continue;int lef=k-__builtin_popcount(mask);if(lef>=n) continue;vector<vector<int>>ve(22,vector<int>(22,0));for(int i=1;i<=n;i++){int idx=1;for(int j=1;j<=n;j++){ve[idx][i]+=w[i][j];if((mask>>j-1)&1) idx++;}}int l=mi,r=ma,res=1e9;while(l<=r){int mid=l+r>>1;bool if1=1;int tlef=lef;unordered_map<int,int>mp;int idx=__builtin_popcount(mask)+1;for(int j=1;j<=n;j++){for(int i=1;i<=idx;i++){countdn--;if(!countdn){cout << ans << "\n"; return ;}mp[i]+=ve[i][j];if(ve[i][j]>mid){if1=0; break;}if(mp[i]>mid && !tlef){if1=0; break;}if(mp[i]>mid && tlef){tlef--;for(int y=1;y<=idx;y++){mp[y]=ve[y][j];if(mp[y]>mid){if1=0; break;}}break;}}if(!if1) break;}if(if1) res=mid,r=mid-1;else l=mid+1;}ans=min(res,ans);}cout << ans << "\n";
}

23年百度之星第五维度 mtj传送门

最开始自己写了个在第一重n的循环里二分，每次二分里再跑遍n，保底 n^2的码，真是糊涂了

思路：直接二分答案，算出所有 s【i】< mid的贡献，减去最大的后判断是否大于m

代码如下：

const int N=2e6+10,M=210;
ll n;
ll m,s[N],v[N];
void solve(){cin >> n >> m;int cnt=0,sumv=0;for(int i=1;i<=n;i++){cin >> s[i] >> v[i];cnt+=(v[i]>0);sumv+=v[i];}if(cnt<=1){cout << "-1"; return ;}ll ans=0;ll l=1,r=4e9;          //4e9为有解最大值while(l<=r){ll mid=l+r>>1;ll ma=0,sum=0;for(int i=1;i<=n;i++){if(s[i]>=mid) continue;sum+=(mid-s[i])*v[i],ma=max((mid-s[i])*v[i],ma);}if(sum-ma>=m) ans=mid,r=mid-1;else l=mid+1;}cout << ans;
}

星期四：

补cf round948 C cf传送门

题意：找出 a的最长子序列使得其 lcm不存在于 a中

思路：很明显我们应该先看整个数组是否可行，如果不行的话，即所有数都是最大数的因子，任意子序列的 lcm也是 an的因子，那么就可检查an的所有因子

找因子是 $\sqrt{a max}$ 的复杂度，最大1e3，对不存在于a中的因子 d进行判断，遍历数组求d的因子的lcm和个数，如果lcm==d，即合法子序列，ans取max

代码如下：

ll n;
int a[2020];
ll ans;
ll lcm(ll x,ll y){return x/__gcd(x,y)*y;
}
void check(int x){ll tlcm=1,len=0;for(int i=1;i<=n;i++){if(a[i]==a[n]) break;if(x%a[i]==0) len++,tlcm=lcm(a[i],tlcm);}if(tlcm==x) ans=max(len,ans);
}
void solve(){cin >> n;unordered_map<int,int>mp;for(int i=1;i<=n;i++){cin >> a[i];mp[a[i]]++;}sort(a+1,a+n+1);for(int i=1;i<n;i++) if(a[n]%a[i]){cout << n << "\n"; return ;}ans=0;for(int d=1;d<=a[n]/d;d++){if(a[n]%d) continue;if(!mp[d]) check(d);if(a[n]/d!=d && !mp[a[n]/d]) check(a[n]/d);}cout << ans << "\n";
}

abc355 D atc传送门

思路：记录所有点，标记下左还是右端点，遍历一遍求得答案

代码如下：

ll n;
vector<PII>ve;
void solve(){cin >> n;for(int i=1;i<=n;i++){int l,r; cin >> l >> r;ve.push_back({l,0});ve.push_back({r,1});}sort(ve.begin(),ve.end());ll ans=0,sum=0;for(auto [x,y]:ve){if(!y) sum++;else ans+=--sum;}cout << ans;
}

星期五：

abc355 F atc传送门

题意：给一无向带权图，初始为一棵树，q次操作，每次操作加一条带权边，每次操作后输出图的最小生成树的边的权值和

思路：注意到边的权值范围很小，用kk的思想，建立10个并查集，第 i个并查集表示边权 <= i的边的联通情况，

代码如下：

const int N=2e6+10,M=210;
ll n;
int fa[N][10];
int fnd(int x,int j){return fa[x][j]==x?x:fa[x][j]=fnd(fa[x][j],j);
}
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++)for(int j=1;j<10;j++) fa[i][j]=i;ll ans=10*(n-1);for(int i=1;i<n+q;i++){int u,v,w; cin >> u >> v >> w;for(int j=w;j<10;j++){int x=fnd(u,j),y=fnd(v,j);if(x!=y) fa[x][j]=y,ans--;else break;}if(i>=n) cout << ans << "\n";}
}

星期六：

百度之星20年 chess mtj传送门

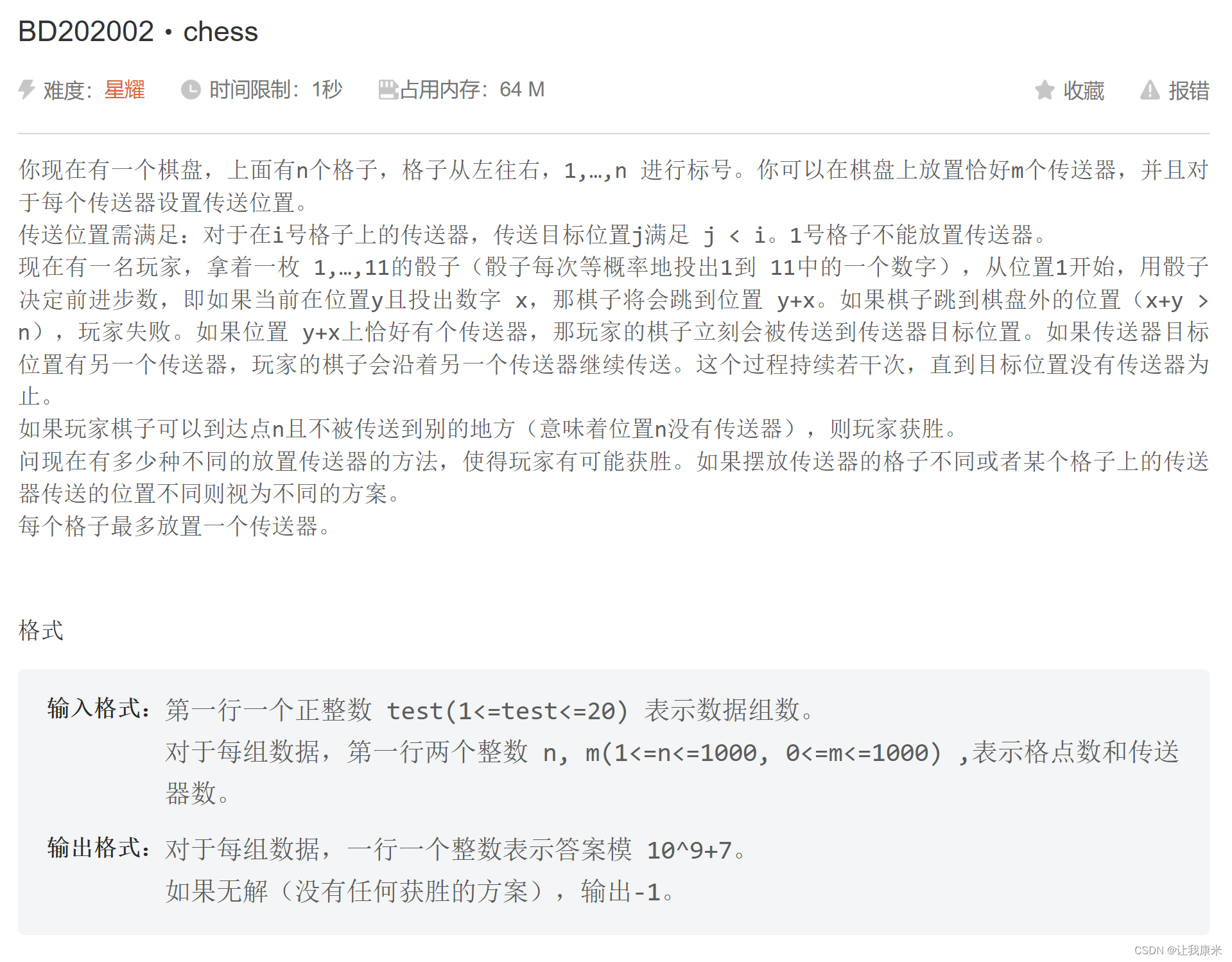
思路：较为简单的dp方案数，dp【i】【j】【k】表示考虑到第 i个格子，放了 j个传送门，最后是连续 k个传送门的情况

有几个需要注意下的点，第一是传送门设置的传送位置不同方案也不同，所以放置传送门时转移需乘上 ( i-1)，第二是内存限制很小，第一维需要滚动，第三是多组样例，记得输出换行符。

代码如下：

ll n;
ll dp[2][1010][12];
void solve(){int m; cin >> n >> m;for(int i=0;i<=1;i++)for(int j=0;j<=m;j++)for(int k=0;k<11;k++) dp[i][j][k]=0;
//	dp[1][0][0]=1;dp[0][0][0]=1;for(int i=2;i<=n;i++){for(int j=0;j<i && j<=m;j++){
//			for(int k=0;k<11;k++) dp[i][j][0]+=dp[i-1][j][k],dp[i][j][0]%=mod;
//			if(j) for(int k=1;k<11;k++) dp[i][j][k]=dp[i-1][j-1][k-1]*(i-1),dp[i][j][k]%=mod;dp[1][j][0]=0;for(int k=0;k<11;k++) dp[1][j][0]+=dp[0][j][k],dp[1][j][0]%=mod;if(j) for(int k=1;k<11;k++) dp[1][j][k]=dp[0][j-1][k-1]*(i-1),dp[1][j][k]%=mod;}for(int j=0;j<i && j<=m;j++)for(int k=0;k<11;k++)dp[0][j][k]=dp[1][j][k];}if(dp[0][m][0]) cout << dp[0][m][0] << "\n";else cout << "-1\n";
}

周日：

百度之星出了俩题，出了道滚动的线性dp 110（多亏chess），然后被硬控一个半小时

线性dp交急了，忘测下n<3的特殊情况，白wa了一发，以后记得提交前尽量测下能想到的样例

！！！！！！！！！！！！！！！！！警钟长鸣啊！！！！！！！！！！！！！！！！！！！

中旬那场打不了，30号还有一场

“ 你觉得你能打赢小星星吗？”