---

🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈｜ 炫酷HTML | JavaScript基础
​💫个人格言: "如无必要，勿增实体"

---

逻辑回归：原理、应用与实践

引言

逻辑回归（Logistic Regression）是一种广泛应用于分类问题的统计学方法，尽管其名称中含有“回归”二字，但它实际上是一种用于解决二分类或多分类问题的线性模型。逻辑回归通过使用逻辑函数（通常为sigmoid函数）将线性模型的输出映射到概率空间，从而预测某个事件发生的概率。本文将深入探讨逻辑回归的理论基础、模型构建、损失函数、优化算法以及实际应用案例，并简要介绍其在机器学习领域的地位和局限性。

1. 逻辑回归基础

1.1 基本概念

逻辑回归主要用于处理因变量为离散型数据的问题，尤其是二分类问题，如判断一个用户是否会购买某产品、一封邮件是否为垃圾邮件等。其核心思想是通过建立输入特征与输出类别之间的逻辑关系模型，来预测输出为某一类别的概率。

1.2 Sigmoid函数

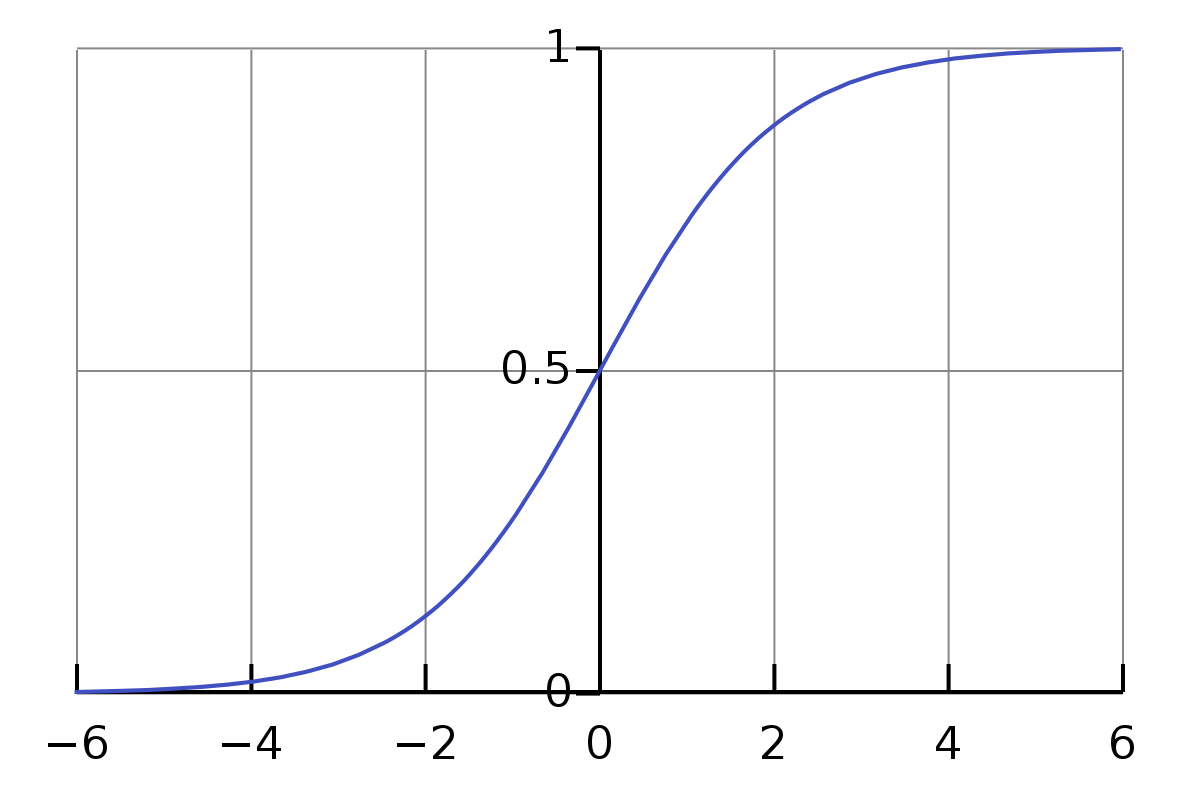
Sigmoid函数是逻辑回归中的关键组件，其表达式为：

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

该函数将线性组合$$z={\theta }^{T}x$$（其中$ \theta $为模型参数，(x)为输入特征向量）的输出映射到(0, 1)之间，可以解释为事件发生的概率。

2. 模型构建

2.1 线性决策边界

逻辑回归模型的形式化表达为：

$$P(Y=1|X=x)=\sigma ({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n)$$

其中，$$(P(Y=1|X=x)$$表示给定特征(x)时，事件发生的概率；(\theta_i)为模型参数，(\theta_0)为截距项。

2.2 参数估计

逻辑回归通过极大似然估计（MLE）来确定模型参数。具体来说，是找到一组参数(\theta)，使得训练数据的似然性最大化。

3. 损失函数与优化

3.1 交叉熵损失函数

逻辑回归常用的损失函数是交叉熵损失（Cross-Entropy Loss），它衡量了模型预测概率分布与真实概率分布的差异。对于二分类问题，损失函数定义为：

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y_i\log (p_i)+(1-y_i)\log (1-p_i)]$$

其中，(m)是样本数量，(y_i)是真实标签，(p_i)是模型预测的概率。

3.2 优化算法

常见的优化算法有梯度下降法及其变种（如批量梯度下降、随机梯度下降、小批量梯度下降）和拟牛顿法等。这些算法通过迭代更新模型参数，以逐步降低损失函数值，达到参数最优解。

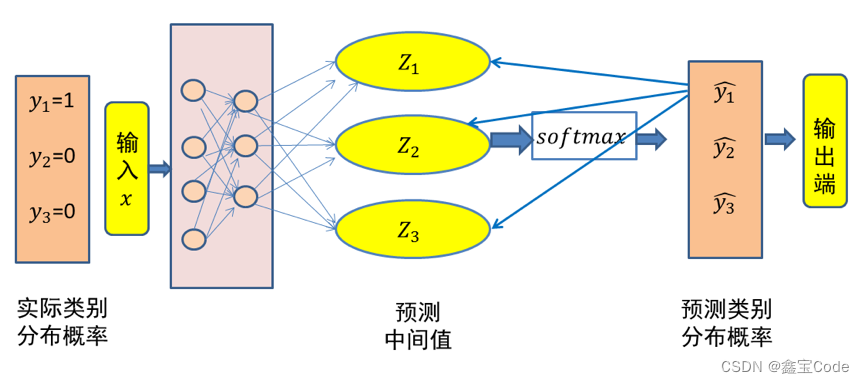
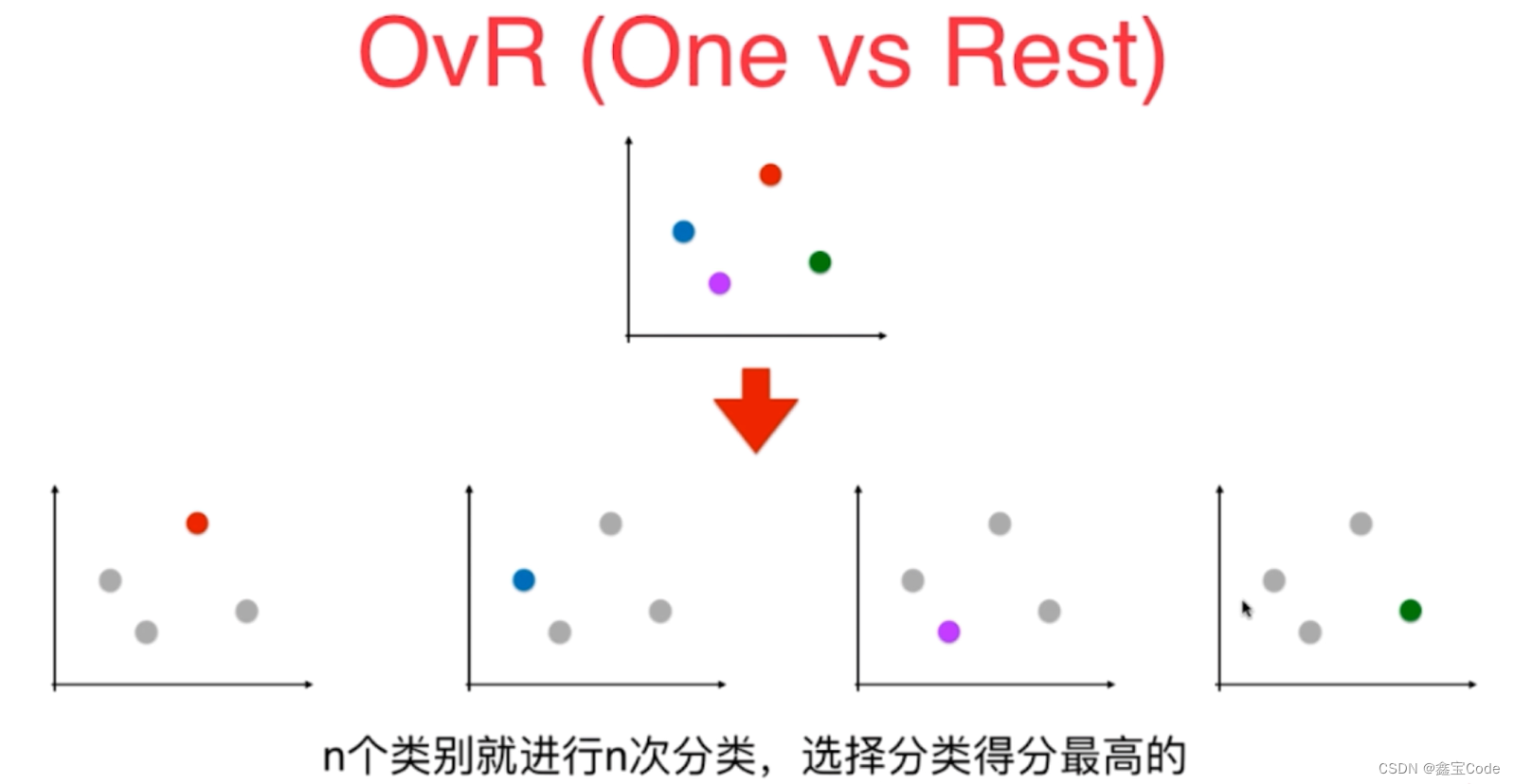
4. 多分类逻辑回归

对于多分类问题，逻辑回归可以通过两种主要方式扩展：一对一（One-vs-One, OvO）和一对多（One-vs-All, OvA）。每种方法都有其适用场景和优缺点。

5. 实践应用与案例分析

5.1 应用领域

逻辑回归因其简单有效，在金融风控、医疗诊断、市场营销等多个领域有着广泛应用。例如，在银行信用评估中，逻辑回归模型可以用来预测客户违约的可能性。

5.2 案例分析

考虑一个简化版的银行贷款申请预测模型。通过收集申请人的年龄、收入、信用评分等特征，利用逻辑回归模型预测申请人是否会违约。通过特征工程、模型训练、交叉验证和调参等步骤，最终得到一个具有较高预测准确率的模型，为银行审批贷款提供决策支持。

首先，请确保安装了scikit-learn库。如果未安装，可以通过pip命令安装：

pip install scikit-learn

然后，你可以使用以下Python代码来实现逻辑回归：

# 导入必要的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.preprocessing import StandardScaler# 加载数据集，这里以鸢尾花数据集为例，但鸢尾花是多分类问题，我们简化为二分类
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :2]  # 只取前两列特征，简化为二维问题
y = (iris.target != 0).astype(int)  # 将目标转换为二分类问题（0和1）# 数据预处理：标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)# 创建逻辑回归模型实例
logreg = LogisticRegression(max_iter=10000)# 训练模型
logreg.fit(X_train, y_train)# 预测测试集结果
y_pred = logreg.predict(X_test)# 输出模型性能指标
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
print("Precision:", metrics.precision_score(y_test, y_pred))
print("Recall:", metrics.recall_score(y_test, y_pred))# 输出模型系数和截距
print("Coefficients:", logreg.coef_)
print("Intercept:", logreg.intercept_)

这段代码演示了如何使用逻辑回归进行二分类任务的基本流程。注意，真实项目中可能需要更复杂的数据预处理和特征工程，以及更细致的模型调整和验证。此外，逻辑回归默认使用的是L2正则化，可以通过调整参数来改变正则化类型或强度。

6. 逻辑回归的局限与挑战

尽管逻辑回归在众多领域表现良好，但其也有一定的局限性：

• 线性假设：逻辑回归假设特征与目标变量间存在线性关系，对于非线性关系可能无法很好地建模。
• 处理大规模特征或高维数据时可能会遇到过拟合问题。
• 对于类别极度不均衡的数据集，需要特别处理以避免模型偏向多数类。

7. 结论

逻辑回归作为经典的机器学习算法之一，凭借其简单、直观且易于实现的特点，在分类任务中依然保持重要地位。尽管面临一些局限性，通过引入正则化、特征选择、非线性变换等手段，逻辑回归能够适应更复杂的实际问题。随着深度学习等新技术的发展，逻辑回归也被融合进更复杂的模型结构中，继续发挥其独特价值。理解逻辑回归不仅有助于掌握基本的机器学习原理，也是深入探索现代机器学习技术的坚实基础。