2024.6.2练习情况—整数二分
一、例题Acwing789.数的范围
题目
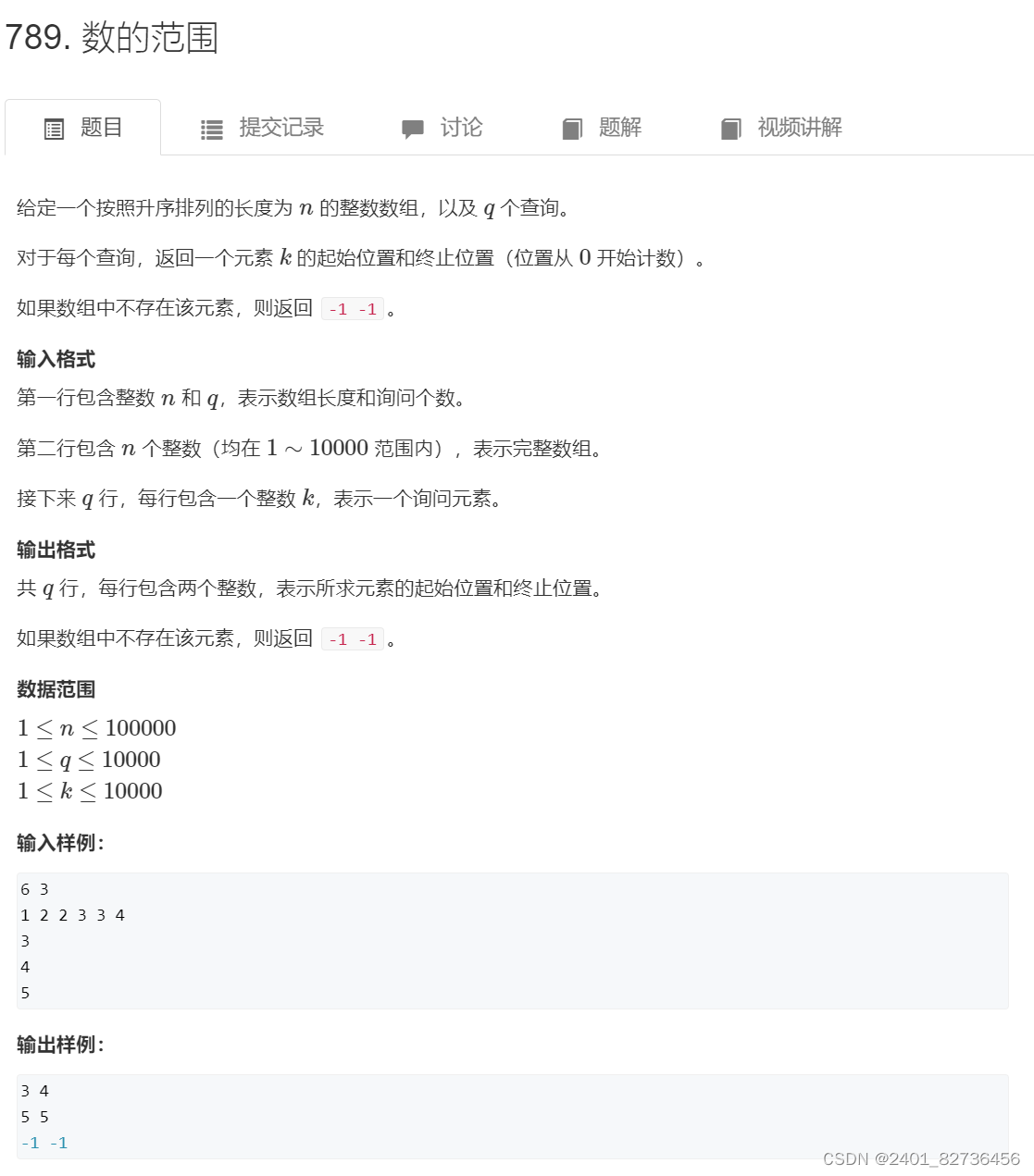
代码
| #include<iostream> #include<cstring> using namespace std; const int N = 100100; int n,q,k;//题中变量 int arr[N]; //找左端点 void querryleft(int arr[],int k){ int l=0,r=n-1;
while(l<r){ int mid=(l+r)/2; if(arr[mid] >= k){ r=mid; } else l=mid+1; } if(arr[l]==k){ printf("%d ",l); } else printf("-1 "); return; } //找右端点 void querryright(int arr[],int k){ int l=0,r=n-1;
while(l<r){ int mid=(l+r+1)/2; if(arr[mid] <= k){ l=mid; } else r=mid-1; } if(arr[l]==k){ printf("%d\n",l); } else printf("-1\n"); return; } int main() { cin>>n>>q; for(int i=0;i<n;i++){ scanf("%d",&arr[i]); } while(q--){ cin>>k; //要求左端点和右端点，若不存在则输出-1 querryleft(arr,k); querryright(arr,k); } return 0; } |
模板核心代码
| //代码2：左端点绿色 int l=0,r=n; while(l<r){ int mid = l+r >> 1; if(check()){ r = mid; } else l = mid + 1; } //代码2：右端点 int l=0,r=n; while(l < r){ int mid = (l+r+1) >> 1; if(check()){ l = mid; } else r = mid - 1; } |
运行评判结果
总结：
完全独立完成。我自己总结了一个整数二分口诀：左端大右，右端小左。要使用二分模板求数段的左端点时，if(check())中的check条件是arr[mid]大于等于被查找数k，并且将右端点缩小，即r=mid；求右端点同理。
二、洛谷P2249 【深基13.例1】查找
题目
- 分析
完全独立完成。题中给出的非负整数序列是单调不减的，并且要求输出要访问数字q在序列中第一次出现的编号。考虑到使用整数二分中求左端点的模板。
代码
| #include<iostream> #include<cstring> using namespace std; const int N = 100000010; int n,q,k;//题中变量 int arr[N]; void querryleft(int arr[],int k){ int l=0,r=n-1;
while(l<r){ int mid=(l+r)/2; if(arr[mid] >= k){ r=mid; } else l=mid+1; } if(arr[l]==k){ printf("%d ",l+1); } else printf("-1 "); return; } int main() { cin>>n>>q; for(int i=0;i<n;i++){ scanf("%d",&arr[i]); } while(q--){ cin>>k; //要求左端点，若不存在则输出-1 querryleft(arr,k); } return 0; } |
运行评判结果
三、洛谷P1102 A-B 数对
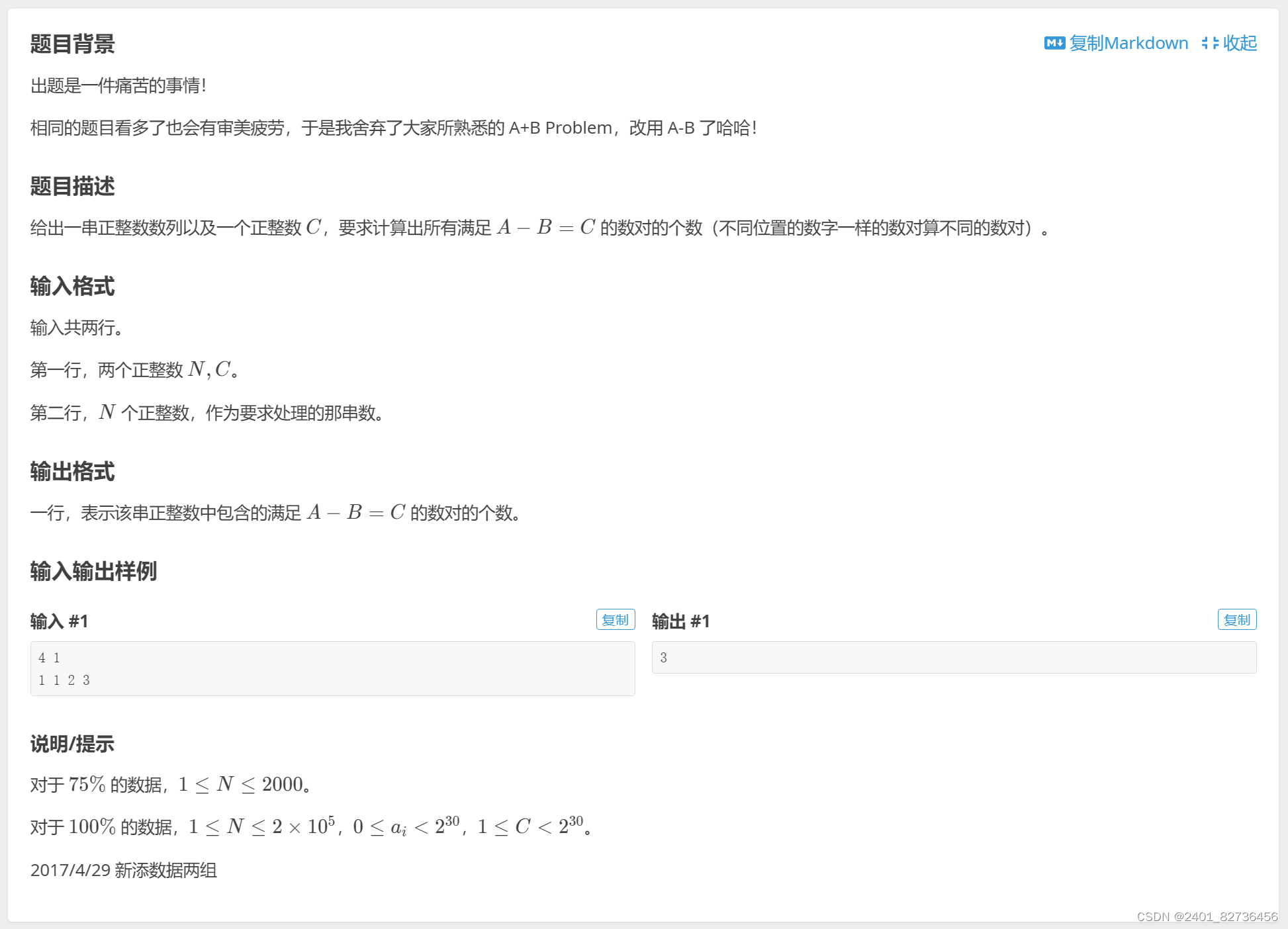
题目
分析
思路1：题目中给出的是一串正整数数列，注意序列是一组顺序排列的东西，若这些东西是数，我们便称之为数列。这道题我的第一想法是用另开一个数组nums，记录每个数字的个数，将A-B=C的形式转成A=B+C，也就是求nums[A]的个数。因为题中说不同位置的数字一样的数对算不同的数对，所以直接循环一遍原数组将nums[A]相加就行。
思路2：学习CSDN上的方法，运用二分知识，先对所有数字排序，然后用一个循环去枚举 A ，枚举A之后呢，就能算出 B = A - C，然后我们只需要知道B的个数即可。用二分知识找到一个数字的起始位置l和终止位置r，那么数字个数就是len = r - l + 1，如果没有找到得到的数量应该是0。然后再把所有的数字加起来即可。
代码
代码1：
| #include<algorithm> #include<iostream> using namespace std; long long n,c; long long a[100000000]; long long nums[1000010]; long long cnt; int main() { scanf("%lld%lld",&n,&c); for(int i=0;i<n;i++){ scanf("%d",&a[i]); nums[a[i]] ++; } sort(a,a+n); for(int i=0;i<n;i++){ cnt += nums[a[i] + c]; } printf("%lld",cnt); return 0; } |
代码2：
| #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int N = 200010; long long ans = 0; int arr[N]; int n,c; //找左端点 int solve1(int x) { int l = 1, r = n; while (l < r) { int mid = (l + r)/2; if (arr[mid] >= x) r = mid; else l = mid + 1; } if (arr[l] != x)return -1; return l; } //找右端点 int solve2(int x) { int l = 1, r = n; while (l < r) { int mid = (l + r + 1)/2; if (arr[mid] <= x) l = mid; else r = mid - 1; } if (arr[l] != x) return -1; return l; } int main() { cin>>n>>c; for (int i = 1; i <= n; i++) { cin>>arr[i]; } sort(arr + 1, arr + 1 + n);
for (int i = 1; i <= n; i++) {// 因为不同位置的数字一样的数对算不同的数对 int x = arr[i] - c; if (x < 1) continue;//如果满足条件的x小于1，则说明不x在数列中 int l = solve1(x); if (l == -1) continue;//如果在数列中 不存在x使得a[i]-x=c,就continue int r = solve2(x); int len = r - l + 1; ans += len; } printf("%lld\n", ans); return 0; } |
运行评判结果
结果1
结果2
![[深度学习]yolov10+deepsort+pyqt5实现目标追踪](https://csdnimg.cn/release/blog_editor_html/release2.3.6/ckeditor/plugins/CsdnLink/icons/icon-default.png?t=N7T8){kind=icon}
