0.前言
本篇文章将详细解释归并排序的原理,以及递归和非递归的代码原理。
一.概念
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
二.具体思想
根据上述所说,我们应当首先将序列不断分为子序列,也就是说将下面的数组分为左右两个部分,然后想办法让左数组有序,右数组有序,之后将这两个数组合并,即可让数组有序。而原数组的左右两部分又可以不断的分割为新的左右数组,那么我们就可以不断的将这个数组分割,直到左右数组内只有一个元素停止。如下图所示:
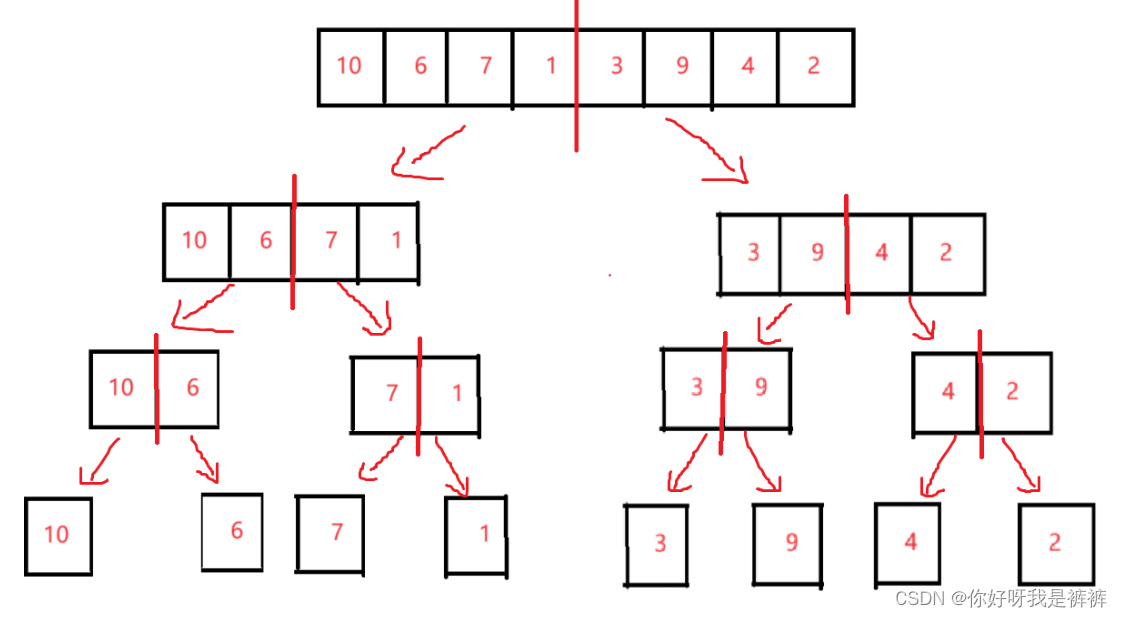
由于现在的左右数组都只有一个元素,那它们各自自然都是有序的,我们就可以将其合并,得到一个有序数组。并不断的进行这个操作,我们即可让原数组有序。以原数组的左子数组为例,我们可做出这些行为:
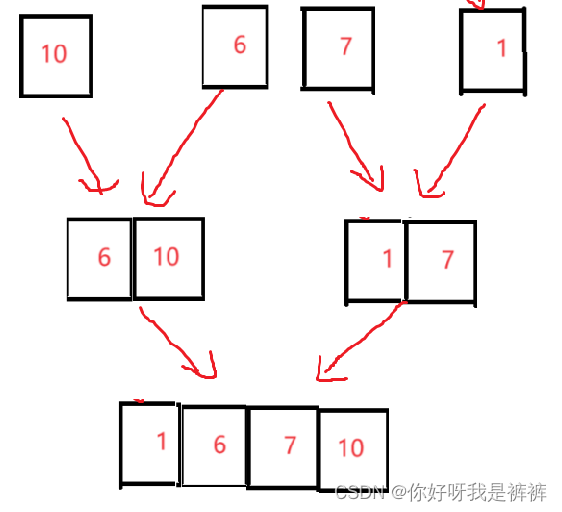
三.做法
现在我们已经理解了他的原理,那么我们应该怎么做呢?
方法1:递归
我们发现,它每次都是将序列分为左右两部分,然后每次都是分为两部分继续遍历,分到不可分割后,我们便不再进行分割,而是进行归并。
而我们二叉树的遍历也是一直分左右子树;而二叉树的后序遍历中则是先将左右都遍历完再进行打印的,我们会发现它们极其类似。
既然如此,我们就可以使用处理二叉树的后序遍历的递归思路来处理这个问题。
根据上述思路,我们可以写出如下代码:
void MergeSort(int* a, int begin,int end)
{ //递归的终止条件if(begin>=end){return;}//分割int mid = (begin + end) / 2;MergeSort(a, begin, mid);MergeSort(a, mid+1, end);//合并//......
}那么,我们下面的工作就是进行合并了。

我们发现,在合并的过程中,在原数组上操作会出现问题,因此我们需要开辟一块空间来保存合并后的数组,因此我们刚刚的函数体的参数列表则不可满足我们的需求。因此我们还应传入一个地址指向一块我们开辟的空间。
void MergeSort(int* a, int begin, int end, int* temp)
{//递归的终止条件if (begin >= end){return;}//分割int mid = (begin + end) / 2;MergeSort(a, begin, mid, temp);MergeSort(a, mid+1,end, temp);//合并
}我们写出的函数是想要拿来就可以直接用的,而不是还需要做一些准备工作才能用。
我们并不想每次开空间时都要先开辟一块空间,这要怎么办呢?
我们可以通过函数的回调来解决这个问题。
void _MergeSort(int* a, int begin, int end, int* temp)
{//递归的终止条件if (begin >= end){return;}//分割int mid = (begin + end) / 2;_MergeSort(a, begin, mid, temp);_MergeSort(a, mid+1,end, temp);//合并//......
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (!temp){perror("malloc fail!");}_MergeSort(a,0,n,temp);
}现在我们就可以做到直接使用了,也不需要传递那么多乱七八糟的参数,只需要将数组的地址和长度传入即可。
那么现在我们来完成我们的归并过程。
我们拿上例中倒数第二趟的归并为例进行分析:
ps:此时两个小数组都已经有序
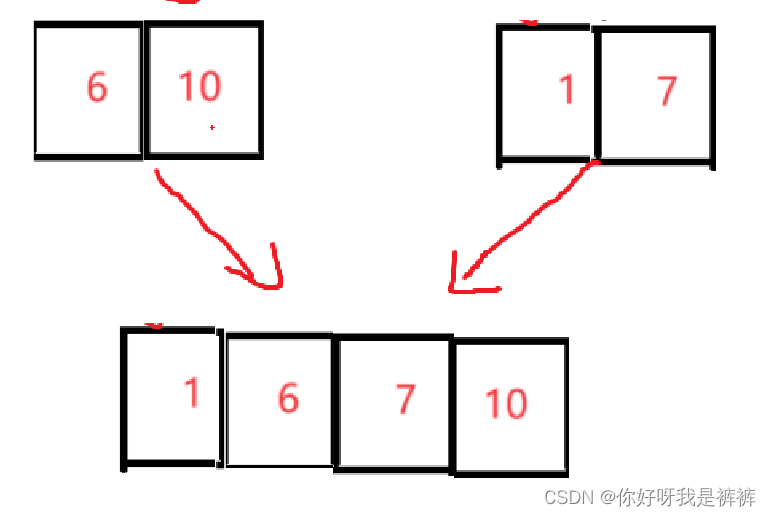
这里我们可以定义两个指针,分别指向两个小数组的第一个元素,然后我们比较指针指向的值,谁小就放到原数组的begin位置,之后再将其指针加1,之后再比较指针的值,直到一方遍历结束,再将另一方的元素拷贝进temp数组即可。过程如下:
过程1:
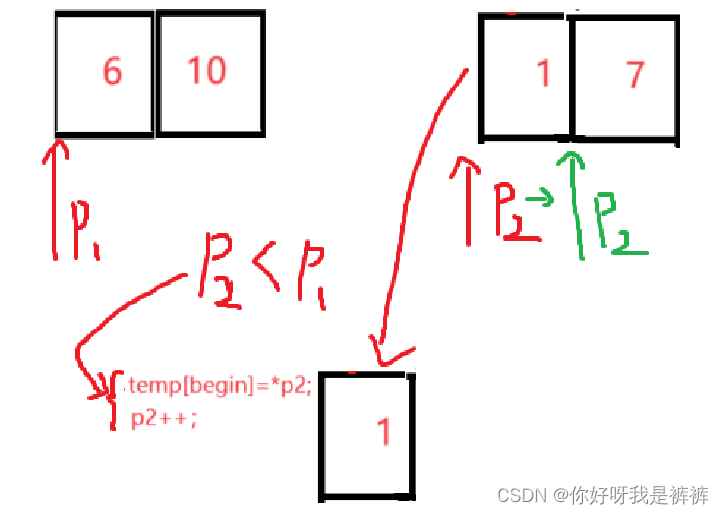
过程2:
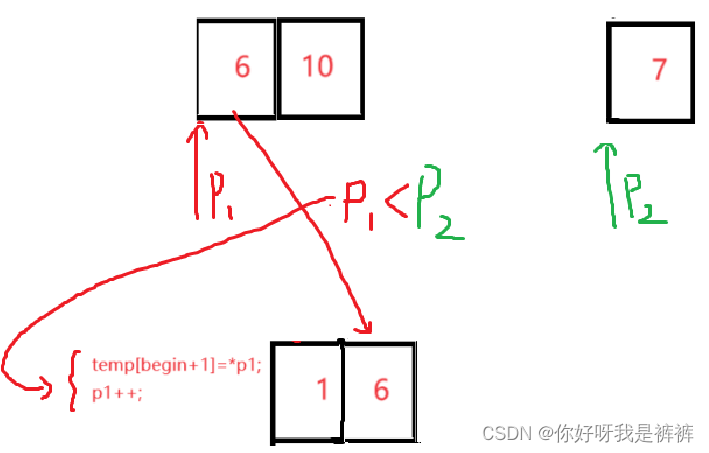
我们下面重复这个操作即可完成对数组的排序。
那么现在我们来完成代码部分:
void _MergeSort(int* a, int begin, int end, int* temp)
{//递归的终止条件if (begin >= end){return;}//分割int mid = (begin + end) / 2;_MergeSort(a, begin, mid, temp);_MergeSort(a, mid+1,end, temp);//合并int begin1 = begin, end1 = mid;//左区间int begin2 = mid + 1, end2 = end;//右区间int i = begin;//用来给temp赋值while (begin1<=end1&&begin2<=end2)//任何一个越界则结束{if (a[begin1] < a[begin2]){temp[i++] = a[begin1++];}if (a[begin2] < a[begin1]){temp[i++] = a[begin2++];}}//一个不越界,另外一个不越界// 下面的while循环必然会进入而且只会进入一个while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}//每次归并完成都要将数据拷贝一份回去memcpy(a+begin,temp+begin,sizeof(int)*(end-begin+1))
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (!temp){perror("malloc fail!");}_MergeSort(a,0,n.temp);
}方法2:非递归
我们现在再来分析一下这一问题。
我们发现,我们会先两个两个分成一组进行排序。

然后再四个四个分成一组进行排序。
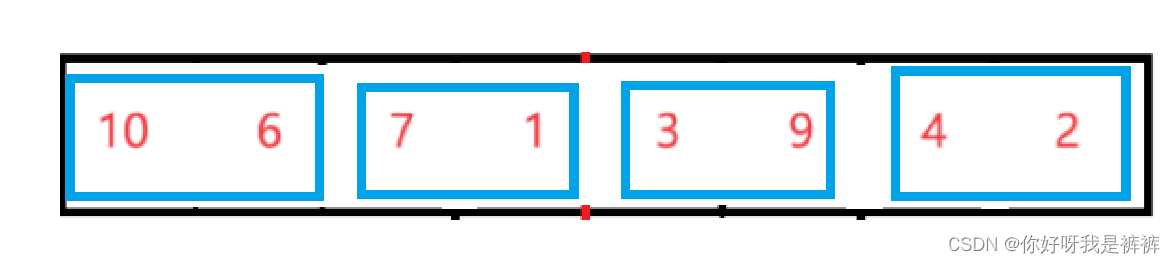
那么我们是否可以通过控制区间来完成这个排序呢?
首先,我们应我们确立一个gap,每次排序完一趟之后都将gap*2,直到gap超过数组的长度。
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}int gap = 1;while (gap < n){//归并代码//......gap *= 2;}
}之后,我们便可以控制单趟的排序了。
我们每趟都是将原数组分为很多对小数组进行比较的,每次比较完毕之后需要跳过一对小数组,直到比较到数组尾为止。
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//比较逻辑//......}gap *= 2;}
}
比较的逻辑和我们递归中的是一样的。
需要我们注意的仅仅只是每一轮的开始处都等于i。
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){ //注意,每一轮的i都相当于递归方法中的beginint begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];}memcpy(a, temp, sizeof(int) * n);gap *= 2;}
}现在我们基本完成了归并排序,最起码,长度为8的数组是能够完成的。
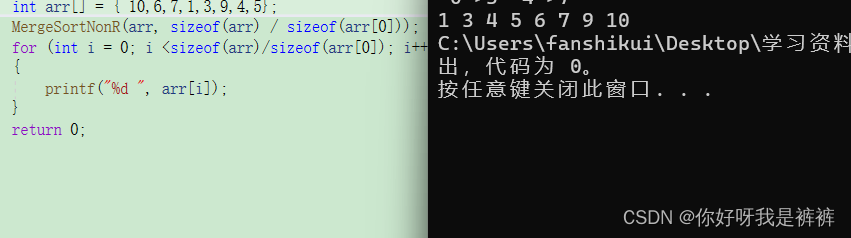
但是还有一个问题需要大家思考:
如果我们的数组长度是10的话,会出现什么样的情况呢?
如下所示:

这是为什么呢?
我们打印一下我们每次比较的区间来看一下

我们发现,出现了越界访问的情况。

通过上图分析,我们可以得到它们越界的情况(begin1不可能越界,因为被外循环限制)
分别如下:
- end2越界
- begin2,end2越界
- end1,begin2,end2越界。
那么我们只要控制好这个边界,即可让这个程序很健壮。
那么我们如何控制这个边界情况呢?
控制方法1:

当end1或begin2越界时,直接跳出循环,不进行归并,未归并的部分就会留存在原数组当中。
如果等到归并结束了之后再整体拷贝temp回原数组,就会覆盖掉没有归并的区域。
为了避免直接将temp中全部元素拷贝回原数组,保持原数组中未被归并部分的数据,
我们要每次归并都拷贝一次数据,而且只拷贝归并的部分。
如果将temp整体拷贝过去的话,上例中下标7后面的数据将会是乱码。
因此我们可以得到如下代码:
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//更改部分if (end1 > n || begin2 > n){break;}if (end2 > n){end = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];memcpy(a + i, temp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}
}控制方法2
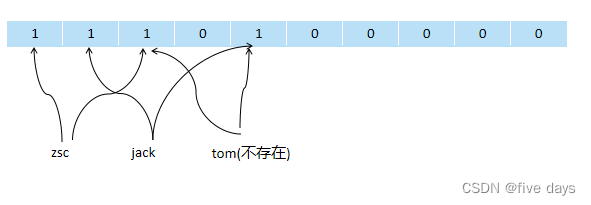
当end1越界时,我们直接将end1设置为数组最后一个元素为止,让begin2和end2为一个不存在的区间。
当begin2越界时,让begin2和end2设置为一个不存在的区间。
当end2越界时,将end2设置为数组最后一个元素。
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){ //注意,每一轮的i都相当于递归方法中的beginint begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n){end1 = n - 1;//[2,1]的区间就寄掉了。begin2 = 2;end2 = 1;}else if (begin2 >= n){begin2 = n;end2 = n - 1;}else if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];}memcpy(a, temp, sizeof(int) * n);//一趟归并一次gap *= 2;}
}这样有个优点在于,每次原数组中的元素被会归并到,每个数据都可以在归并后拷贝到temp数组中,因此我们就可以不像控制方法1那样归并一次拷贝一次了,我们归并一趟之后再拷贝即可。