在我们处理信号过程中最重要的任务就是找到信号隐藏的规律和信号的特征。常用的傅里叶分析法只能用于在时间域或者频率域上分析信号，而通常的数据会在时间域和频率域均有特征。而小波分析是继傅里叶分析之后的一大突破性创新，也是近年来在学术界非常热门的前沿领域，其由于有着深厚的数学理论支撑，又在工程应用中有着优秀的效果，受到了科学界广泛的关注。小波分析的发展推动着多学科的相互渗透、相互结合，也不断带来各领域的新成果。

从信号的处理角度来看，小波分析是一种虽然窗口大小固定但形状可以变化，并且时间窗和频率窗都可以改变的时频分析方法，因此相比于傅里叶变换可以对时频进行局域化分析。

小波变换可以对信号按照不同的频率部分进行更精准的分析，在数据的低频部分为获得有效信息提高频率分辨率，在数据的高频部分为获得有效信息提高时间分辨率。由于小波变换能同时从时间维度和频率维度对信号进行分析，因此理论上拥有可以对任何时间或空间段以及频率段进行任意精度分析的能力。所以相对于傅里叶分析法，小波分析在信号处理的过程中会更为全面的提取信号中潜在的信息，因此将其用于处理非平稳信号通常具有卓越的效果。

鉴于此，采用基于小波区间相关的信号降噪方法对非平稳信号进行降噪，运行环境为MATLAB 2021B，使用与区间相关的阈值对信号进行降噪，包括使用最小阈值对全区间进行降噪，使用最大阈值对全区间进行降噪，手动选择3个阈值对3个区间进行降噪等。

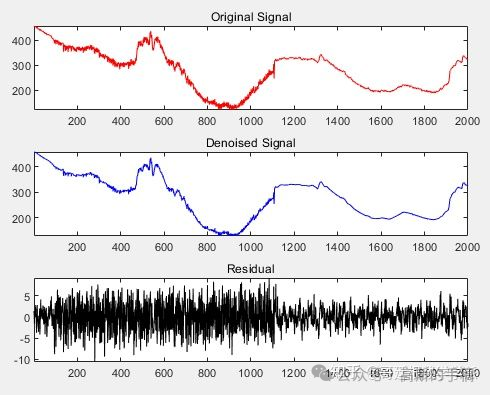
全区间降噪，阈值设置为4.5

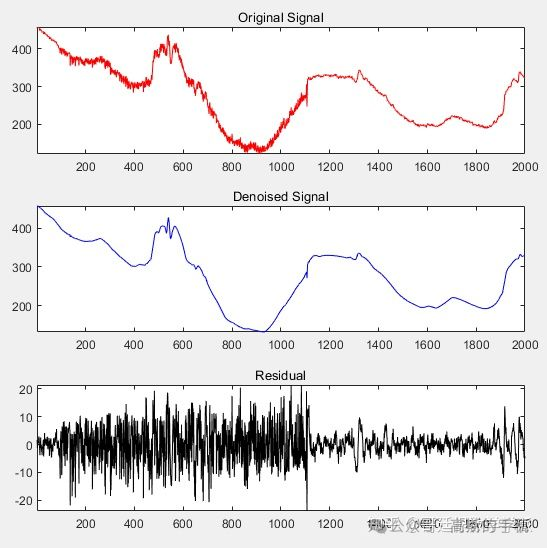
全区间降噪，阈值设置为19.5

使用区间相关阈值 (IDT) 降噪

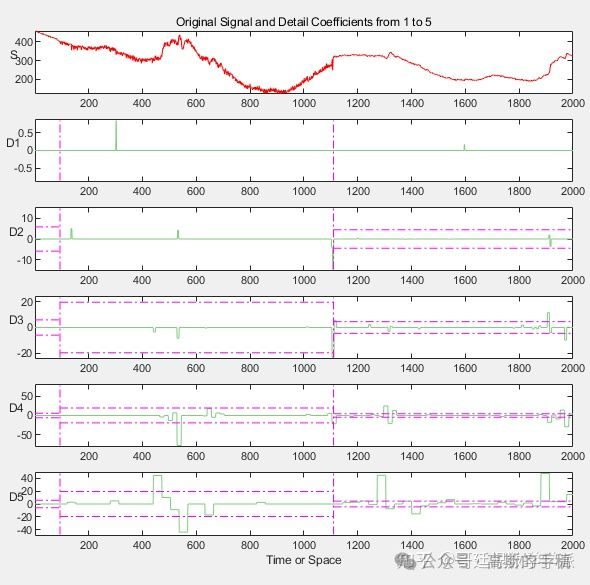
看一下每级小波系数的区间相关阈值

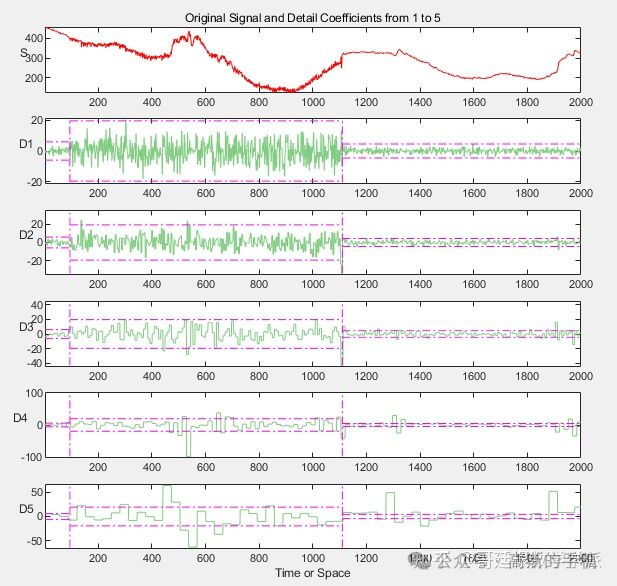
绘制信号经阈值处理后的小波系数

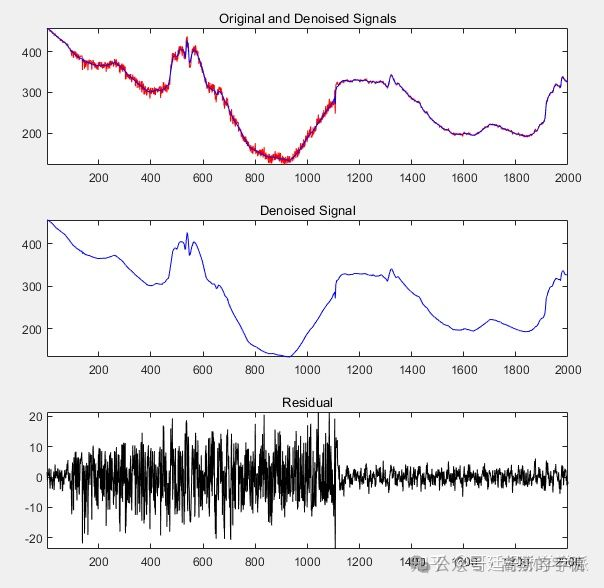
绘制原始信号、降噪信号和残差信号

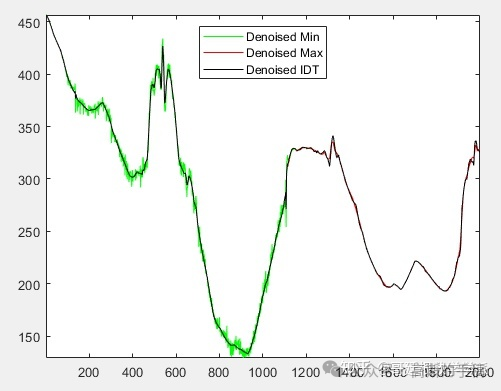
比较信号的三个降噪版本

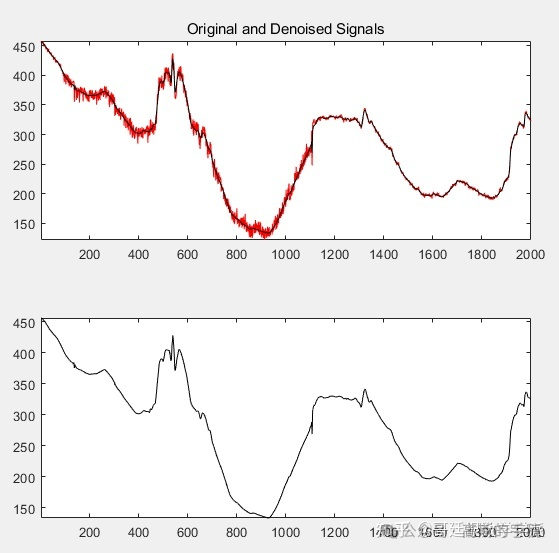
区间相关阈值的自动计算（自动降噪）

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。