【数据结构初阶】栈和队列

1. 栈

1.1 栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）（即最后面进的数据会最先出来）的原则。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。

1.2 栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

  1. 访问效率：数组的随机访问特性意味着可以在常数时间内访问任何位置的元素，这对于栈的操作尤为重要，因为栈的操作总是在栈顶进行。

  2. 空间利用：与链表相比，数组不需要额外的空间来存储指针，这意味着数组的空间利用率更高。

  3. 缓存局部性：由于数组在内存中是连续的，因此具有更好的缓存局部性。当栈顶元素被访问时，相邻的元素也会被加载到缓存中，这可能会提高随后的栈操作的速度。

  4. 实现简单：数组实现栈的逻辑相对简单，不需要维护额外的指针或是节点信息，这使得代码更加简洁，也更容易维护和调试。

  5. 性能考量：在大多数情况下，数组实现的栈在性能上优于链表实现的栈，因为数组的入栈和出栈操作只需要修改栈顶指针，而链表则需要动态分配节点并调整指针。

  6. 空间分配：数组实现的栈在初始化时可能需要分配较大的空间，这可能会导致一定的空间浪费，尤其是在栈的大小远小于数组容量时。然而，这一点可以通过动态扩容的策略来缓解。

此外，在选择栈的实现方式时，除了考虑性能因素外，还需要考虑实际应用场景中的具体需求。例如，如果栈的大小变化非常频繁，那么链表实现可能更为合适，因为链表在插入和删除节点时不需要进行大量的数据复制。然而，如果栈的操作主要是入栈和出栈，并且对性能有较高的要求，那么数组实现将是更好的选择。

支持动态增长的栈：

typedef char STDataType;
typedef struct Stack
{STDataType* _a;int _top;		// 栈顶int _capacity;  // 容量 
}Stack;

 初始化栈 

void StackInit(Stack* ps)
{ps->_a = NULL;ps->_capacity = ps->_top = 0;
}

入栈

void StackPush(Stack* ps, STDataType data)
{assert(ps);if (ps->_capacity == ps->_top){int newcapacity = ps->_capacity == 0 ? 4 : ps->_capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->_a,sizeof(STDataType) * newcapacity);if (tmp==NULL){perror("realloc");return;}ps->_a = tmp;ps->_capacity = newcapacity;}ps->_a[ps->_top] = data;ps->_top++;
}

 出栈

void StackPop(Stack* ps)
{assert(ps);ps->_top--;
}

 获取栈顶元素 

STDataType StackTop(Stack* ps)
{assert(ps);assert(ps->_top > 0);return ps->_a[ps->_top - 1];
}

 获取栈中有效元素个数

int StackSize(Stack* ps)
{assert(ps);return ps->_top;
}

判空

检测栈是否为空，如果为空返回非零结果，如果不为空返回0  

int StackEmpty(Stack* ps)
{assert(ps);if (ps->_top == 0)return 1;elsereturn 0;
}

 销毁栈 

void StackDestroy(Stack* ps)
{assert(ps);free(ps->_a);ps->_a == NULL;ps->_capacity = ps->_top = 0;
}

2. 队列

2.1 队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头。

2.2 队列的实现

队列也可以用数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低（因为数组头上出数据，需要把头后面的数据全部向前移，而链表只需要改变节点的指向就行了）。

链表结构实现队列：

typedef struct QListNode
{struct QListNode* _next;QDataType _data;
}QNode;// 队列的结构 
typedef struct Queue
{QNode* _front;QNode* _rear;int size;
}Queue;
初始化队列 
void QueueInit(Queue* q)
{assert(q);q->_front = NULL;q->_rear = NULL;q->size = 0;
}
 队尾入队列
QNode* SLBuyNode(QDataType data)
{QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc");return;}newNode->_next = NULL;newNode->_data = data;return newNode;
}void QueuePush(Queue* q, QDataType data)
{QNode* newNode = SLBuyNode(data);if (q->_front == NULL){q->_front = q->_rear = newNode;q->size++;}else{q->_rear->_next = newNode;q->_rear = q->_rear->_next;q->size++;}
}
队头出队列 
void QueuePop(Queue* q)
{assert(q&&q->_front);QNode* next = q->_front->_next;free(q->_front);if (next == NULL)q->_front = q->_rear = next;elseq->_front = next;q->size--;
}
 获取队列头部元素 
QDataType QueueFront(Queue* q)
{assert(q && q->_front);return q->_front->_data;
}
 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{assert(q && q->_rear);return q->_rear->_data;
}
 获取队列中有效元素个数
int QueueSize(Queue* q)
{QNode* head = q->_front;int count = 0;while (head){head = head->_next;count++;}return count;
}
 判空

检测队列是否为空，如果为空返回非零结果，如果非空返回0 

int QueueEmpty(Queue* q)
{if (q->_front == NULL)return 1;elsereturn 0;
}
 销毁队列
void QueueDestroy(Queue* q)
{assert(q);while (q->_front){QNode* next = q->_front->_next;free(q->_front);q->_front = next;}q->_rear = NULL;
}

3. 栈和队列的面试题

3.1 队列实现栈

. - 力扣（LeetCode）

解题思路：

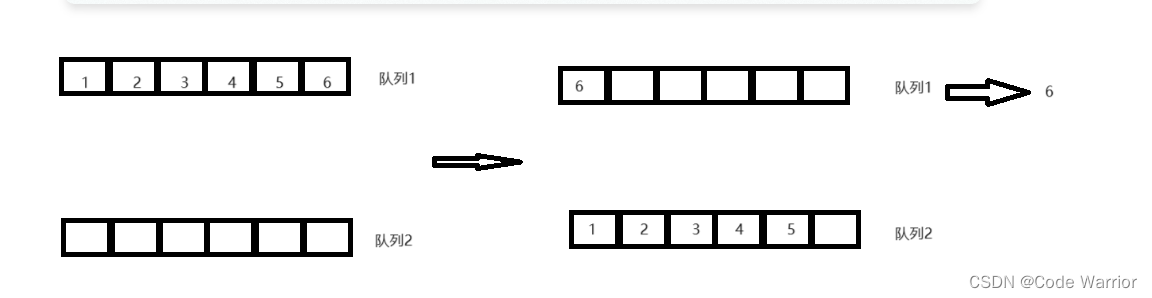
队列中的数据遵循先进先出的原则，而栈中的数据遵循后进先出的原则，所以要想队列实现栈，就需要让队列实现数据的后进先出，这时候我们就可以设置两个队列，其中一个队列入数据，当出数据的时候，就把除了最后一个数据的所有数据放到另一个队列中，然后从队列1出数据，这样就实现了后进先出。（如下图）

还有一个问题就是当入数据的时候该往哪个队列入数据呢？

如果是往空队列入数据的话，空队列就变成了非空队列，这样就会导致两个队列都是非空队列，而无法分辨下一次该往哪个队列入数据。而往非空队列入数据则避免了这一情况，当然如果两个队列都为空，那就随便往一个队列入数据就可以了。

typedef int QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{struct QListNode* _next;QDataType _data;
}QNode;// 队列的结构 
typedef struct Queue
{QNode* _front;QNode* _rear;int size;
}Queue;// 初始化队列 
void QueueInit(Queue* q)
{assert(q);q->_front = NULL;q->_rear = NULL;q->size = 0;
}QNode* SLBuyNode(QDataType data)
{QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc");return 0;}newNode->_next = NULL;newNode->_data = data;return newNode;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{QNode* newNode = SLBuyNode(data);if (q->_front == NULL){q->_front = q->_rear = newNode;q->size++;}else{q->_rear->_next = newNode;q->_rear = q->_rear->_next;q->size++;}
}
// 队头出队列 
void QueuePop(Queue* q)
{assert(q&&q->_front);QNode* next = q->_front->_next;free(q->_front);if (next == NULL)q->_front = q->_rear = next;elseq->_front = next;q->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{assert(q);assert(q->_front);return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{assert(q);assert(q->_rear);return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{QNode* head = q->_front;int count = 0;while (head){head = head->_next;count++;}return count;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{if (q->_front == NULL)return 1;elsereturn 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{assert(q);while (q->_front){QNode* next = q->_front->_next;free(q->_front);q->_front = next;}q->_rear = NULL;
}typedef struct {Queue q1;Queue q2;
} MyStack;MyStack* myStackCreate() {MyStack* pst = (MyStack*)malloc(sizeof(MyStack));QueueInit(&pst->q1);QueueInit(&pst->q2);return pst;
}void myStackPush(MyStack* obj, int x) {if(QueueEmpty(&obj->q1)==0){QueuePush(&obj->q1, x);}else{QueuePush(&obj->q2, x);}
}int myStackPop(MyStack* obj) {Queue* Empty = &obj->q1;Queue* nonEmpty = &obj->q2;if(QueueEmpty(&obj->q1)==0){Empty = &obj->q2;nonEmpty = &obj->q1;}while(nonEmpty->size>1){QueuePush(Empty, QueueFront(nonEmpty));QueuePop(nonEmpty);}int top = QueueFront(nonEmpty);QueuePop(nonEmpty);return top;
}int myStackTop(MyStack* obj) {if(QueueEmpty(&obj->q1)==0){return QueueBack(&obj->q1);}elsereturn QueueBack(&obj->q2);
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);free(obj);
}

3.2 用栈实现队列

题目描述：

. - 力扣（LeetCode）

解题思路： 

栈中的数据遵循后进先出的原则，而队列中的数据遵循先进先出的原则，所以要想用栈实现栈，就需要让栈实现数据的先进先出，如下图我们可以设置两个栈，一个栈存放数据，另一个栈出数据。具体实现是：往非空的栈插入数据，出数据的时候将栈1的数据导入栈2，然后从栈2出数据，最后将栈的数据导回栈1，因为不导回数据的话根据栈后进先出的原则，会将插入的数据倒过来，如果直接将数据插入栈2，就会导致栈插入的数据顺序被打乱。

typedef int QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{struct QListNode* _next;QDataType _data;
}QNode;// 队列的结构 
typedef struct Queue
{QNode* _front;QNode* _rear;int size;
}Queue;// 初始化队列 
void QueueInit(Queue* q)
{assert(q);q->_front = NULL;q->_rear = NULL;q->size = 0;
}QNode* SLBuyNode(QDataType data)
{QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc");return 0;}newNode->_next = NULL;newNode->_data = data;return newNode;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{QNode* newNode = SLBuyNode(data);if (q->_front == NULL){q->_front = q->_rear = newNode;q->size++;}else{q->_rear->_next = newNode;q->_rear = q->_rear->_next;q->size++;}
}
// 队头出队列 
void QueuePop(Queue* q)
{assert(q&&q->_front);QNode* next = q->_front->_next;free(q->_front);if (next == NULL)q->_front = q->_rear = next;elseq->_front = next;q->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{assert(q);assert(q->_front);return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{assert(q);assert(q->_rear);return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{QNode* head = q->_front;int count = 0;while (head){head = head->_next;count++;}return count;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{if (q->_front == NULL)return 1;elsereturn 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{assert(q);while (q->_front){QNode* next = q->_front->_next;free(q->_front);q->_front = next;}q->_rear = NULL;
}typedef struct {Queue q1;Queue q2;
} MyStack;MyStack* myStackCreate() {MyStack* pst = (MyStack*)malloc(sizeof(MyStack));QueueInit(&pst->q1);QueueInit(&pst->q2);return pst;
}void myStackPush(MyStack* obj, int x) {if(QueueEmpty(&obj->q1)==0){QueuePush(&obj->q1, x);}else{QueuePush(&obj->q2, x);}
}int myStackPop(MyStack* obj) {Queue* Empty = &obj->q1;Queue* nonEmpty = &obj->q2;if(QueueEmpty(&obj->q1)==0){Empty = &obj->q2;nonEmpty = &obj->q1;}while(nonEmpty->size>1){QueuePush(Empty, QueueFront(nonEmpty));QueuePop(nonEmpty);}int top = QueueFront(nonEmpty);QueuePop(nonEmpty);return top;
}int myStackTop(MyStack* obj) {if(QueueEmpty(&obj->q1)==0){return QueueBack(&obj->q1);}elsereturn QueueBack(&obj->q2);
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);free(obj);
}

3.3 设计循环队列

题目描述：

. - 力扣（LeetCode）

解题思路： 

typedef struct {int*_a;int head;int tail;int k;
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* tmp = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));tmp->_a = (int*)malloc(sizeof(int)*(k+1));tmp->head=0;tmp->tail=0;tmp->k=k;return tmp;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if((obj->tail+1)%(obj->k+1)==obj->head)return false;obj->_a[obj->tail] = value;obj->tail = (obj->tail+1)%(obj->k+1);return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(obj->tail==obj->head){return false;}obj->head = (obj->head+1)%(obj->k+1);return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if(obj->head==obj->tail){return -1;}return obj->_a[obj->head];
}int myCircularQueueRear(MyCircularQueue* obj) {if(obj->head==obj->tail){return -1;}return obj->_a[(obj->tail+obj->k)%(obj->k+1)];
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->head==obj->tail;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->tail+1)%(obj->k+1)==obj->head;
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->_a);free(obj);obj->_a==NULL;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/344958.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

HTML开发 Vue2.x + Element-UI 动态生成表单项并添加表单校验

HTML开发 Vue2.x + Element-UI 动态生成表单项并添加表单校验

基于vue2.x 和element-ui 动态生成表单项并添加表单校验； 1、需求问题 如下图，项目有个需求，点击添加按钮，新增一行设备信息，且每项信息必填； 2、代码 看到这个需求，首先想到要使用v-for的形…
阅读更多...
springboot集成uid-generator生成分布式id

springboot集成uid-generator生成分布式id

一、简介 uid-generator是由百度技术部开发,GitHub地址 UidGenerator是Java实现的, 基于Snowflake算法的唯一ID生成器 Snowflake算法 Snowflake算法描述：指定机器 & 同一时刻 & 某一并发序列，是唯一的。据此可生成一个64 bits的唯一ID&#x…
阅读更多...
Windows 宿主机访问 VirtualBox 虚拟机中创建的 docker 容器中的 mysql8.0 的数据

Windows 宿主机访问 VirtualBox 虚拟机中创建的 docker 容器中的 mysql8.0 的数据

一、场景需求 在开发环境中，一般使用 windows 系统进行开发，但需要在 linux 系统中创建运行 mysql8.0 的 docker 容器中进行测试（win10特定版本或win11才能安装 docker），为了方便还需要在 windows 系统中通过 SQLyog …
阅读更多...
Python轻量级嵌入式关系数据库之apsw使用详解

Python轻量级嵌入式关系数据库之apsw使用详解

概要 在现代应用开发中，数据库是一个非常重要的组成部分。SQLite 是一个轻量级的嵌入式关系数据库管理系统，被广泛应用于各种应用程序中。APSW（Another Python SQLite Wrapper）库是一个专门用于访问 SQLite 数据库的 Python 包，它提供了 SQLite 所有的功能，并且比标准库…
阅读更多...
【教学类-40-01】20240607类似MJ的免费AI绘画工具——文心一格与通义万相

【教学类-40-01】20240607类似MJ的免费AI绘画工具——文心一格与通义万相

背景需求： 风变的AI对话大师一年到期了，也没有看到续费的按钮。不能使用它写代码了。 MJ早就用完了，最后480次，我担心信息课题会用到它生图，所以不敢用。 最近探索其他类似MJ的免费出图工具 一、文心一格（…
阅读更多...
各种空气能热泵安装图

各种空气能热泵安装图

空气能热泵安装图 循环式空气能热泵安装图 直热循环式空气能热泵安装图 泳池空气能热泵安装图 循环式水源热泵热安装系统原理图 直热循环式水源热泵安装系统图 空气水源热泵安装图
阅读更多...
XUbuntu24.04之ch9344(usb转串口芯片)安装驱动(二百四十五)

XUbuntu24.04之ch9344(usb转串口芯片)安装驱动(二百四十五)

简介： CSDN博客专家，专注Android/Linux系统，分享多mic语音方案、音视频、编解码等技术，与大家一起成长！ 优质专栏：Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏：多媒…
阅读更多...
如何将本地项目上传到GitHub

如何将本地项目上传到GitHub

在软件开发过程中，将本地项目上传到GitHub是一个非常重要的步骤。它不仅可以帮助你备份代码，还可以让你与团队成员共享和协作开发。本文将详细介绍如何将本地项目上传到GitHub。 前提条件 已安装Git。如果还没有安装，请参考Git官网进行下载…
阅读更多...
【linux】信号（三）

【linux】信号（三）

本章节将会围绕信号处理进行展开讲解 目录 回顾一下：历史问题：地址空间：键盘的输出如何被检测到：持续更新... 回顾一下： 信号处理也就是信号递达 我们说过递达时一种有3种行为 默认行为忽略行为自定义行为 历史问…
阅读更多...
JVM之【字节码/Class文件/ClassFile 内容解析】

JVM之【字节码/Class文件/ClassFile 内容解析】

说在前面的话 字节码/Class文件/ClassFile 均为同一概念 Java语言:跨平台的语言(write once,run anywhere) 当Java源代码成功编译成字节码后，如果想在不同的平台上面运行，则无须再次编译这个优势不再那么吸引人了。Python、PHP、Perl、Ruby、Lisp等有…
阅读更多...
28-LINUX--I/O复用-epoll

28-LINUX--I/O复用-epoll

一.epoll概述 epoll 是 Linux 特有的 I/O 复用函数。它在实现和使用上与 select、poll 有很大差异。首 先，epoll 使用一组函数来完成任务，而不是单个函数。其次，epoll 把用户关心的文件描述 符上的事件放在内核里的一个事件表中。从而无需像…
阅读更多...
xshell远程无法链接上VM的centos7

xshell远程无法链接上VM的centos7

1、现象如下， 2.解决办法：查证后发现这个默认的设置为vmnet0 3.参考文章：Xshell连接不上虚拟机centos7_centos7的nat模式可以ping通网络,但是用xshell连不上是什么原因-CSDN博客
阅读更多...
QT C++（QT控件 QPushButton，QRadioButton，QCheckBox）

QT C++（QT控件 QPushButton，QRadioButton，QCheckBox）

文章目录 1. QPushButton 普通按钮2. QRadioButton 单选按钮3. QCheckBox 复选按钮 1. QPushButton 普通按钮 QPushButton中的重要属性 text：按钮中的文本icon：按钮的图标iconSize：按钮中图标的尺寸shortCut：按钮对应的快捷键&a…
阅读更多...
STM32编程：实现LED灯闪烁（基于手写SDK的方式）

STM32编程：实现LED灯闪烁（基于手写SDK的方式）

项目结构 stm32f10x.h 文件 //寄存器的值常常是芯片外设自动更改的，即使CPU没有执行程序，也有可能发生变化 //编译器有可能会对没有执行程序的变量进行优化//volatile表示易变的变量，防止编译器优化， #define __IO volati…
阅读更多...
【IC验证】03 UVM

【IC验证】03 UVM

阅读更多...
53.ReentrantLock原理

53.ReentrantLock原理

ReentrantLock使用 ReentrantLock 实现了Lock接口， 内置了Sync同步器继承了AbstractQueuedSynchronizer。 Sync是抽象类，有两个实现NonfairSync非公平，FairSync公平。 所以ReentrantLock有公平锁和非公平锁。默认是非公平锁。 public sta…
阅读更多...
我的编程语言学习记录：一段不断探索的旅程

我的编程语言学习记录：一段不断探索的旅程

目录 我的编程语言学习记录：一段不断探索的旅程 1.引言 2.我的编程之旅开始 第一站：Python — 简洁之美 第二站：JavaScript — 网页的魔法 第三站：Java — 企业级的力量 3.学习过程中的挑战与克服 1.理解概念 3.记忆语法…
阅读更多...
读书笔记：左耳听风

读书笔记：左耳听风

程序员如何用技术变现 我完全没有必要通过打工听人安排而活着，而是反过来通过在公司工作提高自己的技能，让自己可以更为独立和自由地生活。 因而，在工作当中，对于那些没什么技术含量的工作，我基本上就像是在学生时代那…
阅读更多...
Java 的循环

Java 的循环

Java 有三种循环&#xff1a;for&#xff0c;while&#xff0c;do while。 for 基本语法&#xff1a; for (循环变量初始化; 循环条件; 循环变量迭代){循环语句; }程序示例&#xff1a; public static void main(String[] args) {for (int i 0, j 0; i < 3; i, j--) {…
阅读更多...
即时设计工具对决：Figma、Sketch与XD的优劣比较

即时设计工具对决：Figma、Sketch与XD的优劣比较

最近几年&#xff0c;UI 设计工具出现了许多后起之秀&#xff0c;其中有四款更具代表性的UI设计软件&#xff1a;Sketch、Adobe XD、Figma 和 即时设计&#xff0c;这四个设计软件都有自己的优势。如果合作对您的UI设计过程至关重要&#xff0c;那么Figma 和 即时设计 它应该是…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023