题目:39. 组合总和
这道题目和组合差不多
通过上述startIndex的方法 可以避免出现path(里面元素一样但是顺序不一样)重复的情况
本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
本题搜索的过程抽象成树形结构如下: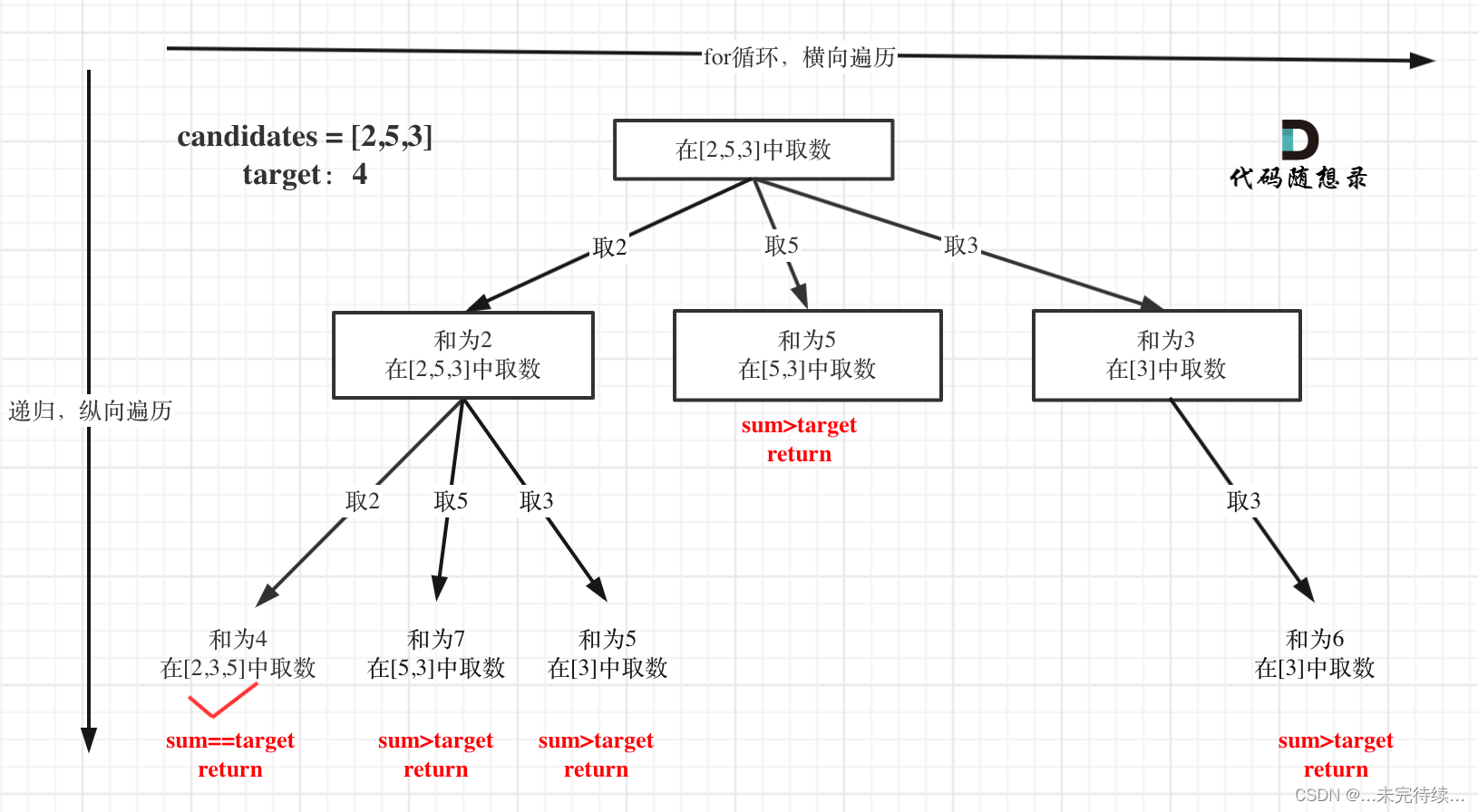
完整代码如下:
// 版本一
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum > target) {return;}if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates, target, 0, 0);return result;}
};题目:40. 组合总和 II
这道题目要考虑去重的部分 因为候选集合的元素里是有重复的元素 并且每个元素只能用一次所以对于候选集合无重复的用原来的方法不会有重复但是对于有重复的候选集合 用原来的方法就会有重复
startIndex 可以保证候选集合里的元素不重复使用
当初自己想的vector删除指定位置的元素和恢复指定位置的元素
int position = 2; // 例如,删除索引为2的元素(即第3个元素)
// 使用erase方法删除指定位置的元素
numbers.erase(numbers.begin() + position);
// 恢复原来的值
numbers.insert(numbers.begin() + position, removed_value);正确的初始化方式
vector<int> used(candidates.size(), 0); // 正确初始化 used 向量 显示初始化数组大小然后才是数值
这边去重的理解看文字比较难理解 结合视频看一下
需要注意的是树层去重的话需要要先把候选集合排序一下 排序默认升序 然后新建一个used数组用于保存是否使用的情况
回溯算法中的去重,树层去重树枝去重,你弄清楚了没?| LeetCode:40.组合总和II_哔哩哔哩_bilibili
完整代码如下:
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序,让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};题目:131. 分割回文串
这道题要多练练 不熟
切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
所以直接递归进行切割 然后切割到叶子节点之后用双指针的方法判断每个叶子节点是不是回文串即可 这就是大概的思路
所以切割问题,也可以抽象为一棵树形结构,如图:
这题是必须找到每个子串都是 回文串 其中任意一个不是都不行 因此只有当startIndex

从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
所以终止条件代码如下:
void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了 即每个字串都是回文 一旦有一个不是那么startIndex就不会超过s.size()因此一旦startIndex >= s.size()就说明找到了一组分析方法if (startIndex >= s.size()) {result.push_back(path);return;}
}来看看在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。 因为i会逐渐增大
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
这里要注意一下如何在字符串中获取子串
for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 如果不是则直接跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}注意切割过的位置,不能重复切割所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
最后我们看一下回文子串要如何判断了,判断一个字符串是否是回文。
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。 注意right是减减
完整如下
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};