目录
🌞0.前言
🚈1.二叉树链式结构的代码是实现
🚈2.二叉树的遍历及代码实现和深度刨析代码
🚝2.1前序遍历
✈️2.1.1前序遍历的理解
✈️2.1.2前序代码的实现
✈️2.1.3前序代码的深度解剖
🚝2.2中序遍历
✈️2.2.1中序遍历的理解
✈️2.2.中序代码的实现
🚝2.3后序遍历
✈️2.3.1后序遍历的理解
✈️2.3.2后序代码的实现
🚈3.层序遍历
🚝 3.1层序遍历的代码实现
🚈4.二叉树学习的相关建议和方法
✍5.结束语
🌞0.前言
言C之言,聊C之识,以C会友,共向远方。各位博友的各位你们好啊,这里是持续分享数据结构知识的小赵同学,今天要分享的数据结构知识是二叉树的前中后序和层序,在这一章,小赵将会向大家展开聊聊二叉树的前中后序和层序的相关知识。✊
🚈1.二叉树链式结构的代码是实现
有了前面几篇博客的加持,我们也算是对于二叉树有了清晰的认识,在这样的情况下,我们就可以尝试用链表去实现我们的二叉树了。
如这样一棵二叉树

我们该如何实现呢,其实实现起来也容易,就是创建每一个节点,然后用手动把他们连起来,其的操作方法和我们之前的链表很像。
typedef int treenode;
typedef struct BTNode
{int x;//本身存储的数据struct BTNode*left;//左孩子struct BTNode* right;//右孩子
}BTNode;BTNode* BuyNode(int a)//生成一个节点
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));//申请一个空间if (newnode == NULL){perror("malloc failed");return;}newnode->left = NULL;//先默认左右孩子为空newnode->right = NULL;newnode->x = a;return newnode;//返回节点
}
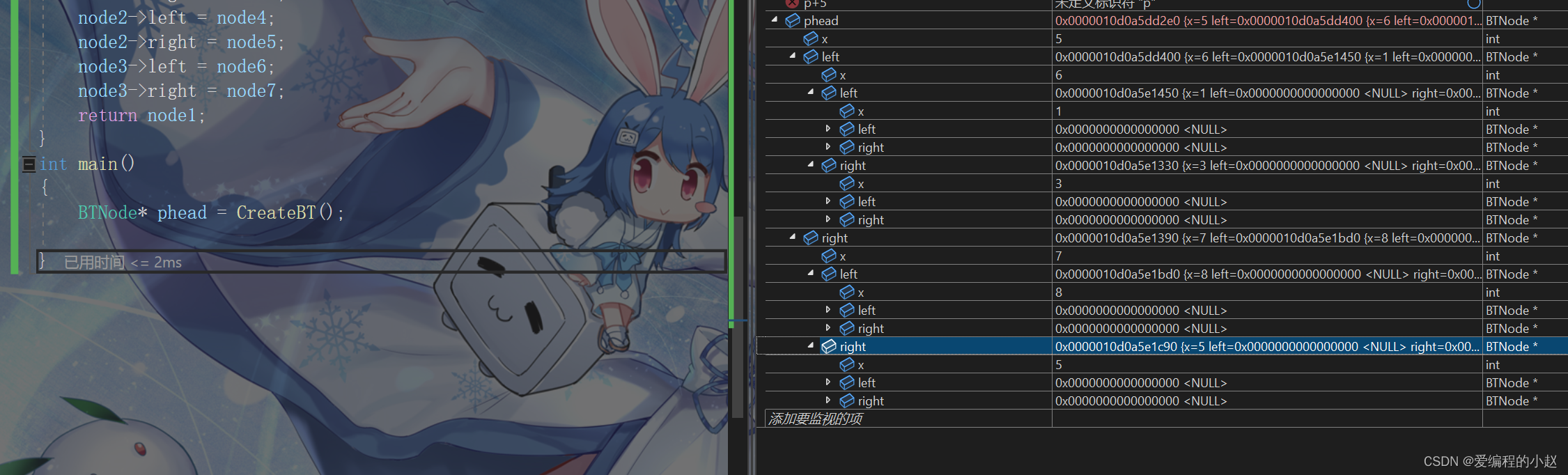
BTNode* CreateBT()
{BTNode* node1 = BuyNode(5);//生成需要的节点BTNode* node2 = BuyNode(6);BTNode* node3 = BuyNode(7);BTNode* node4 = BuyNode(1);BTNode* node5 = BuyNode(3);BTNode* node6 = BuyNode(8);BTNode* node7 = BuyNode(5);node1->left = node2;//将节点连起来node1->right = node3;node2->left = node4;node2->right = node5;node3->left = node6;node3->right = node7;return node1;
}
int main()
{BTNode* phead = CreateBT();}这样我们就可以建立我们的链表了。
🚈2.二叉树的遍历及代码实现和深度刨析代码
那我们有了一棵树,现在我想遍历这个树的数据怎么办呢?这个时候我们就提出了三种遍历方式叫前中后序遍历。
🚝2.1前序遍历
✈️2.1.1前序遍历的理解
那么前序是怎么遍历的呢?叫根左右,什么叫做根左右呢?就是先遍历一棵树的根部,再遍历这棵树的左子树,左子树遍历完了,再遍历这棵树的右子树。
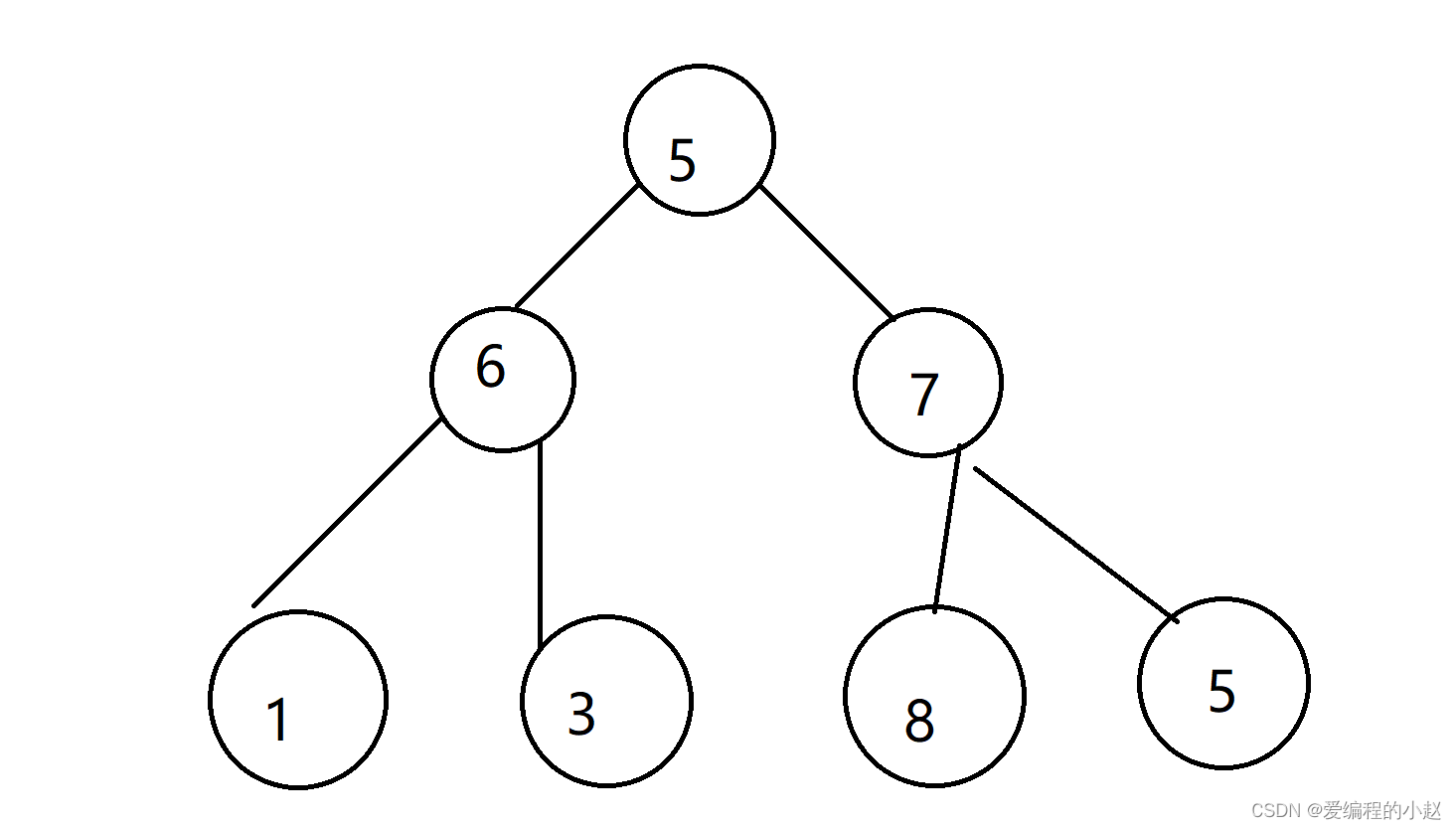 那么对于像我们这棵树的遍历顺序是什么呢?如果用前序遍历的话是5613785
那么对于像我们这棵树的遍历顺序是什么呢?如果用前序遍历的话是5613785
相信这个答案很多人会很惊讶,为什么会是这样呢?其实小赵一开始也是这样,但只要一步步弄懂了,就会觉得不难了。
首先我们遍历这棵树的根部就是5,这个大家应该都没问题。
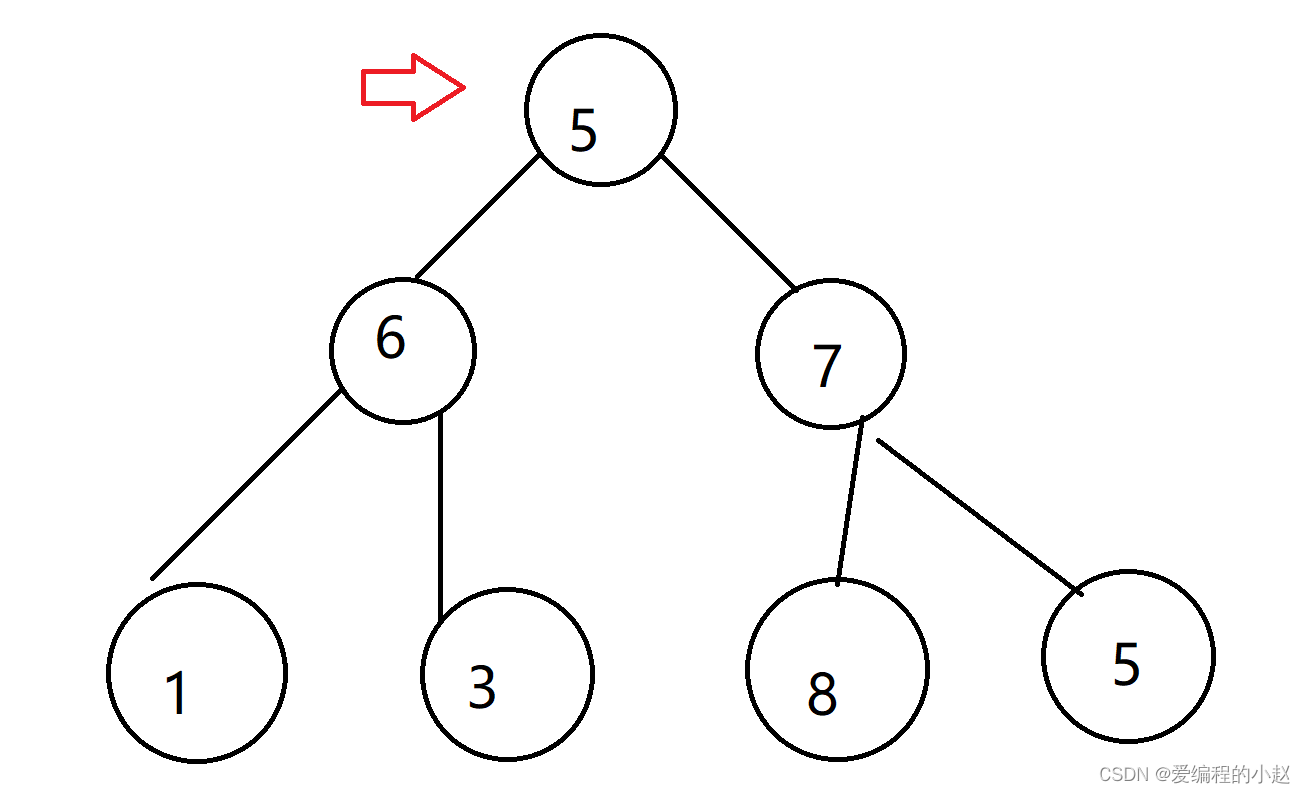
那么接下来我们要干嘛要遍历左子树对不对,那我们就进入左子树进行遍历。这个时候的遍历方法其实就是把它的左子树单独看。
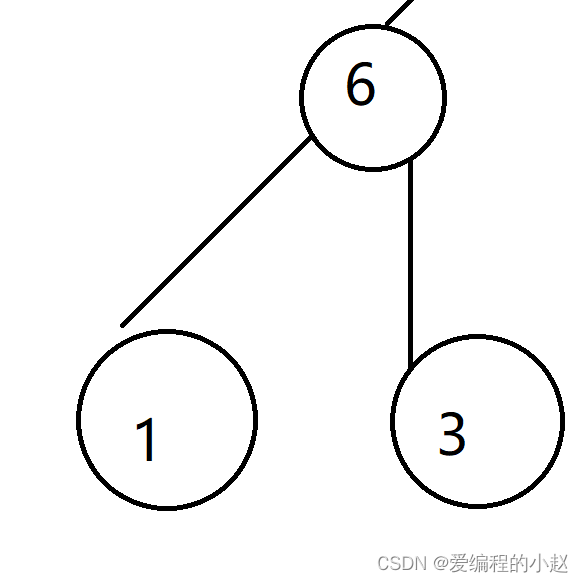
好了那么我们怎么遍历左子树呢?还是那个方法啊,先遍历根,根是谁,6,那么5之后就是6。然后我们接着遍历这颗树的左子树,又是根开始就是1,那么6之后就是1。下面遍历1的左子树,我们发现1的左子树没了,那接着遍历右子数,我们发现1的右子树也没了,这个时候我们1这棵子树已经遍历完成了。我们发现对于6来说,1的这棵左子树已经遍历完成了,那就遍历6的右子数,也就是3,等到3也遍历完了,那么6的左右子数就遍历完了,对于最上面的5的根来说,它的左子树就遍历完成了,接着去遍历右子数,还是按照我们遍历左子树的方法去进行遍历。

✈️2.1.2前序代码的实现
void PreOrder(BTNode* root)
{if (root==NULL)//看这个节点是否是空节点{return;//是返回}printf("%d", root->x);//遇到根打印PreOrder(root->left);//遍历左子树PreOrder(root->right);//遍历右子树
}看到这个代码的,我的头一阵晕,因为我怎么都无法想象一个这么大的遍历最后实现的代码会这么短。我也很难去进入到这个递归代码的里面去找寻原因,后来我发现一个方面是我的对于深层次的递归可能脑子有点记不住前面的递归,还有一个方面就是我不知道这个函数的返回问题。最终我也是在b站,百度上找到了解决这个问题的办法,这个办法就是递归展开图。
✈️2.1.3前序代码的深度解剖
什么叫递归展开图呢?其实就是把隐藏的代码表示出来,因为我们要无数次的重新进入这个函数,那不如就把每一次的递归场景画出来。

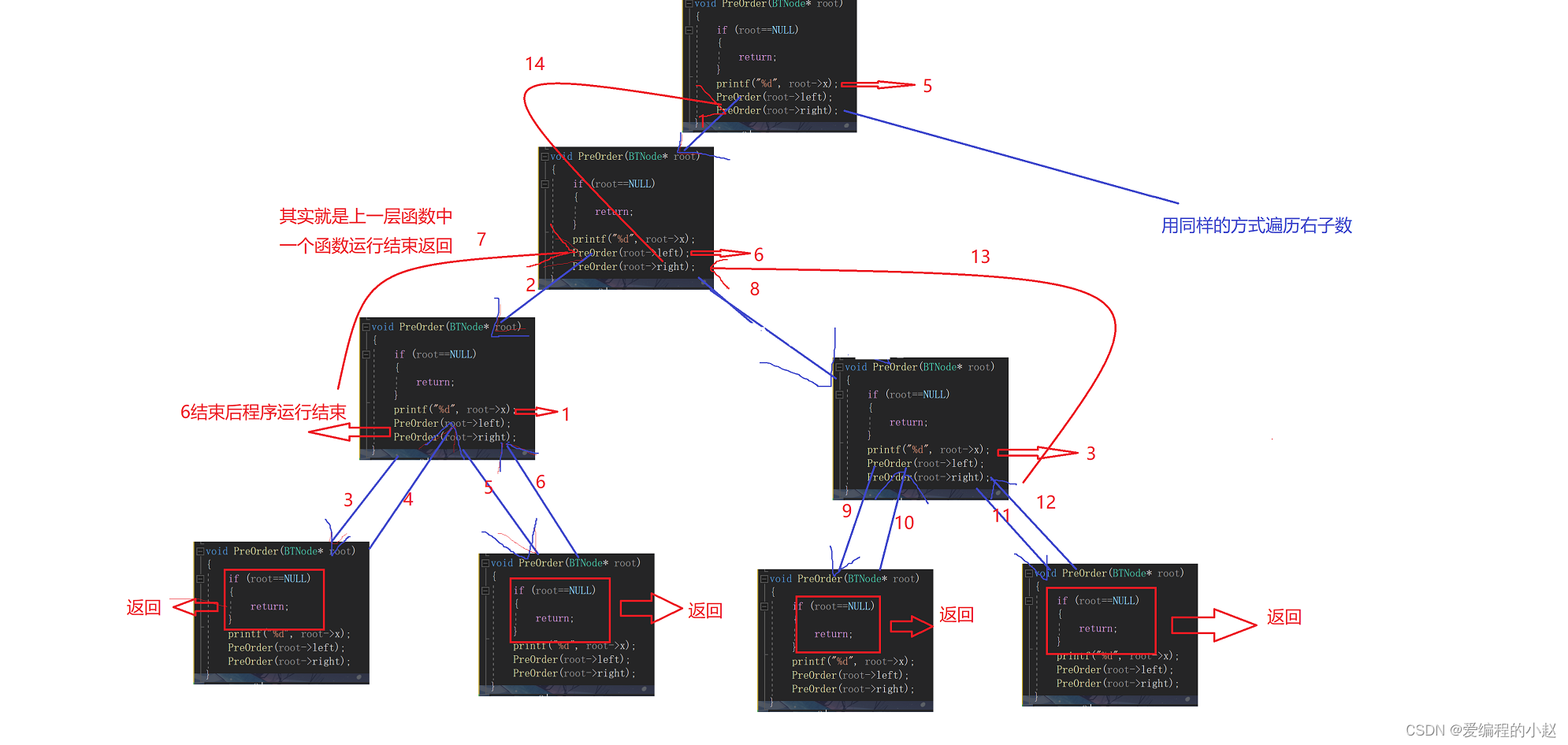
这里呢小赵就演示了一下左子树的递归展开图的方式,下面的中序后序也是一样的
所以下面小赵可能就不再进行这样的演示,大家可以自行操作,这个的操作软件就是我们电脑上都有的画图软件。
大家可以先将我们的代码截屏一下,然后在画图软件里面用ctrl+v就可以出现很多一样的图了。然后自己用上面的工具去操作还是非常好用的。
🚝2.2中序遍历
✈️2.2.1中序遍历的理解
那么中序是怎么遍历的呢?叫左根右,什么叫做左根右呢?相信大家也都猜出来了就是先遍历一棵树的左子树,遍历完了左子树,再遍历这棵树的根,最后遍历右子树。
其实如果前序能理解这个也大差不差,但是这里有一个点要注意其实和上面的前序遍历一样只有访问根才能接触到数据,遍历其实是接触不到的。
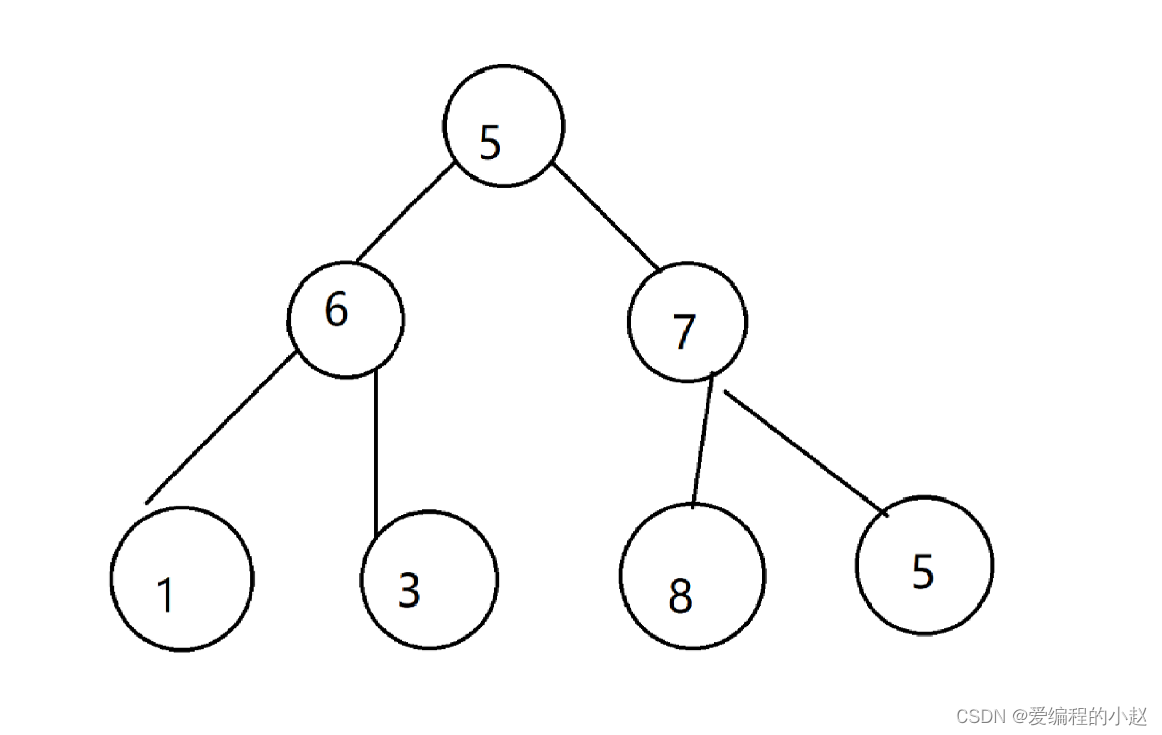
例如这个图如果按中序先遍历左树,5就不是第一个。而要遍历5的左子树。

那么其的访问方式其实和我们之前遍历是很像的,我们一直遍历一棵树的左子树,知道其中一棵的左子树遍历没了,我们就开始访问这棵树的根节点,这个时候对我们这个图来说就是1作为第一个数据
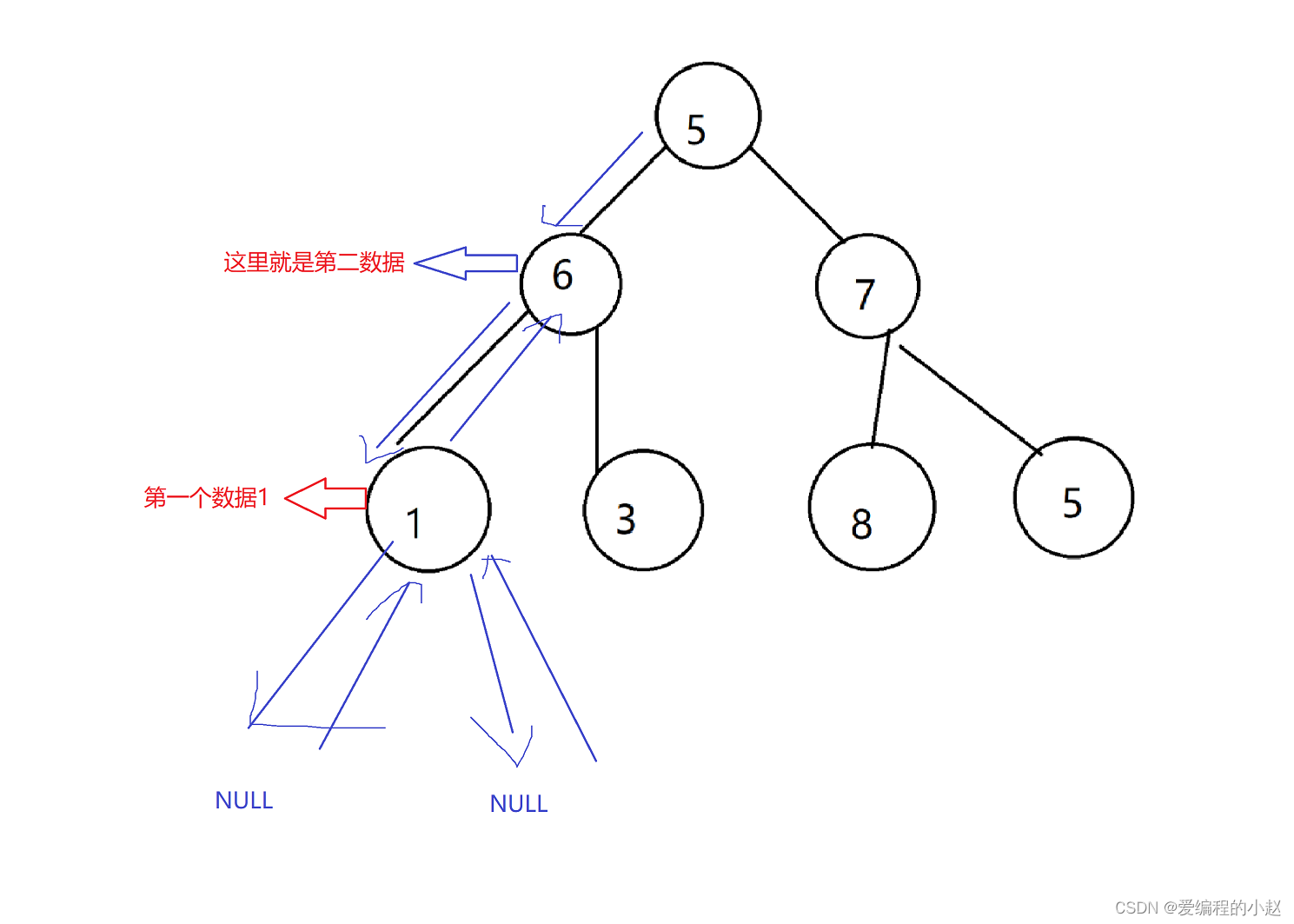
那么我们最后中序遍历的结果其实是1635875
✈️2.2.中序代码的实现
中序代码的实现
void InOrder(BTNode* root)
{if (root == NULL)//看看这个节点是不是空节点{return;}InOrder(root->left);//遍历左子树printf("%d", root->x);//访问根节点InOrder(root->right);//遍历右子树
}然后这个代码小赵也是非常推荐大家去按照小赵上面的方法去画递归展开图,虽然初期递归展开图很费时间和经历但对于你去理解二叉树的前中后序是绝对非常有帮助的。
🚝2.3后序遍历
✈️2.3.1后序遍历的理解
后序遍历就是左右根(其实这个时候我们发现记忆前序中序和后序不难只需要想根节点的位置就行。)
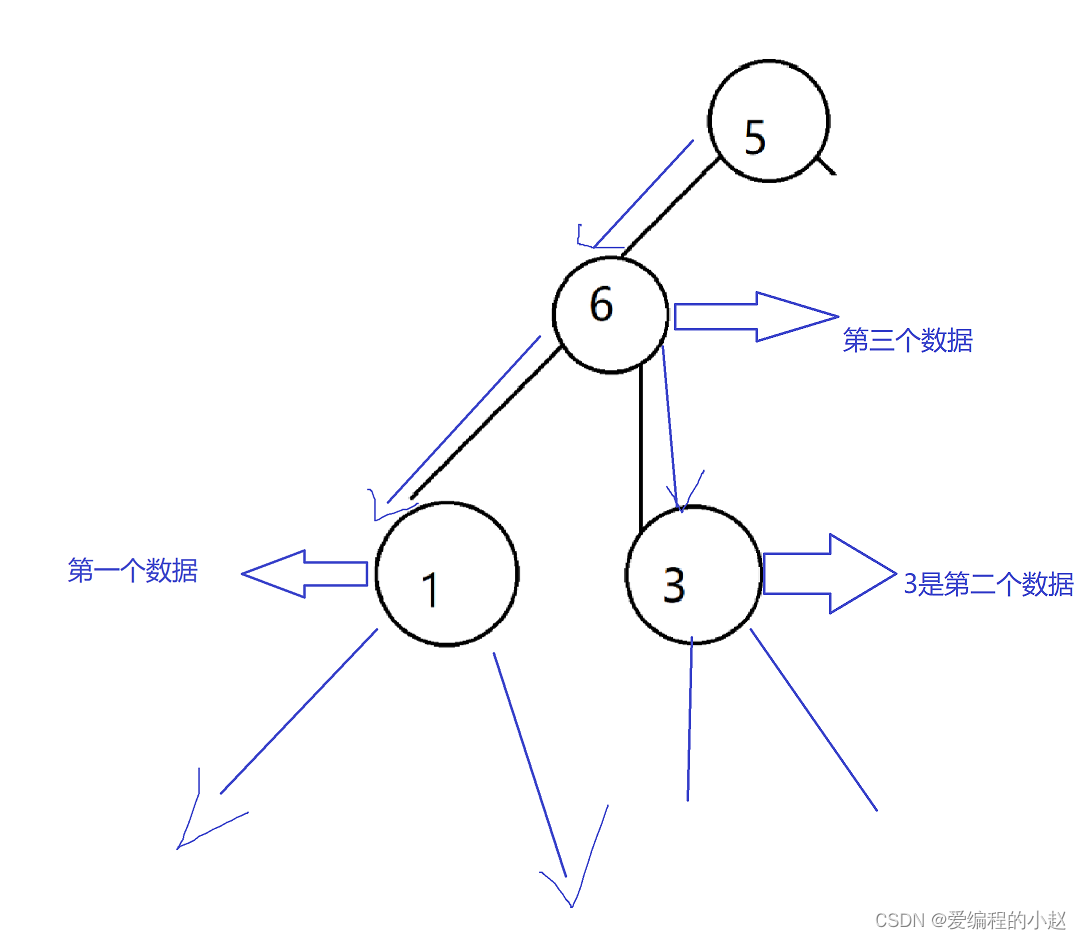
然后按这种方式遍历,我们会发现最上面的5是最后遍历的,其实相对于任何一棵树都是,根是最后遍历的,因为它必须先遍历左子树和右子树才能访问到根节点。’
然后后序遍历的结果是:1368575
✈️2.3.2后序代码的实现
void PostOrder(BTNode* root)
{if (root == NULL)//看看这个节点是不是空节点{return;}PostOrder(root->left);//遍历左子树PostOrder(root->right);//遍历右子树printf("%d", root->x);//访问根节点
}这个也是一样要画画递归展开图。
🚈3.层序遍历
之所以把层序遍历拿出来聊,是因为我感觉这个东西和前面的前中后序还是不大一样,正如它的名字所言,它是一层一层遍历的,在实现的方法上也不是我们之前的递归。
层序遍历的具体方式如下:
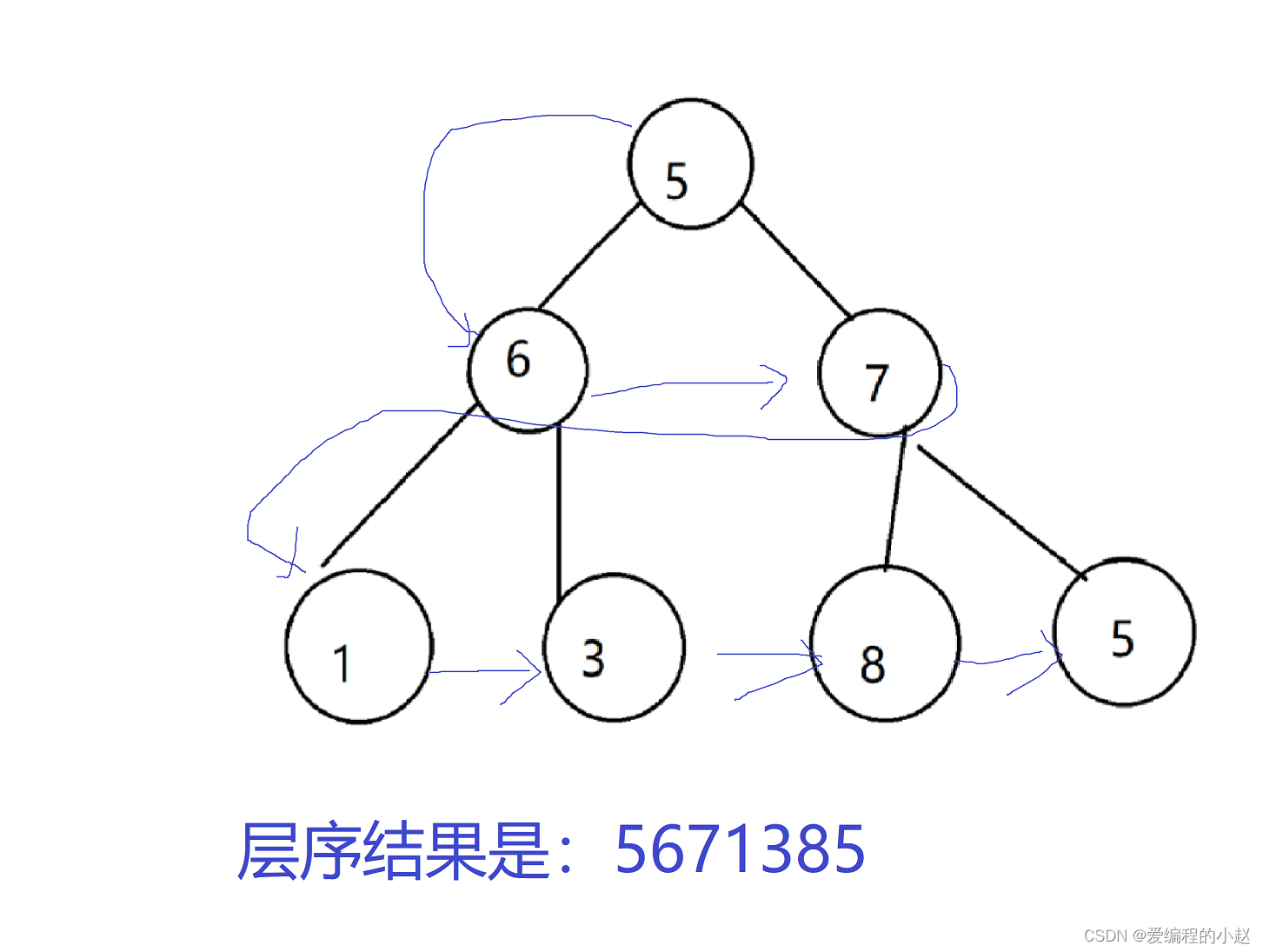
✈️🚝✈️ 3.1层序遍历的代码实现
那么层序遍历主要使用的是什么方法呢?其实是我们的队列,为什么使用队列呢?因为使用队列有一个好处就是先进先出,我们可以让我们的根节点先进去,然后根据根节点,插入我们的左子树和右子树,然后把根节点数据打印出来,然后在进入下一个阶段,左子树把下面两个带入,自己出去。

那么按这样的顺序,5出来后6,7就会进入,6出去后,1,3就会进入,然后是7进入,就可以完美的完成我们的遍历任务了。
因为这里要用到队列,所以小赵就先把前面的代码拷了过来,各位想要实现列表可以看看前面的文章数据结构(c):队列 http://t.csdnimg.cn/Px3yF ,小赵在里面已经非常详细地说明了其的实现方法,这里唯一要注意的是要把里面存的数据改成我们的节点。
typedef BTNode* QDataType;void LevelOrder(Queue* Qphead, BTNode* BTphead)
{QueuePush(Qphead, BTphead);//将根节插入队列中while (!QueueEmpty(Qphead)){if (BTphead == NULL){return;}QueuePush(Qphead, BTphead->left);//将根节点的左右子数插入队列QueuePush(Qphead, BTphead->right);int data = BTphead->x;//拿到该节点的数据QueuePop(Qphead);//在队列中删除该节点printf("%d", data);//打印节点BTphead = QueueFront(Qphead);//拿到下一个节点}
}
int main()
{BTNode* phead = CreateBT();Queue* head = (Queue*)malloc(sizeof(Queue));QueueInit(head);//初始化队列LevelOrder(head, phead);
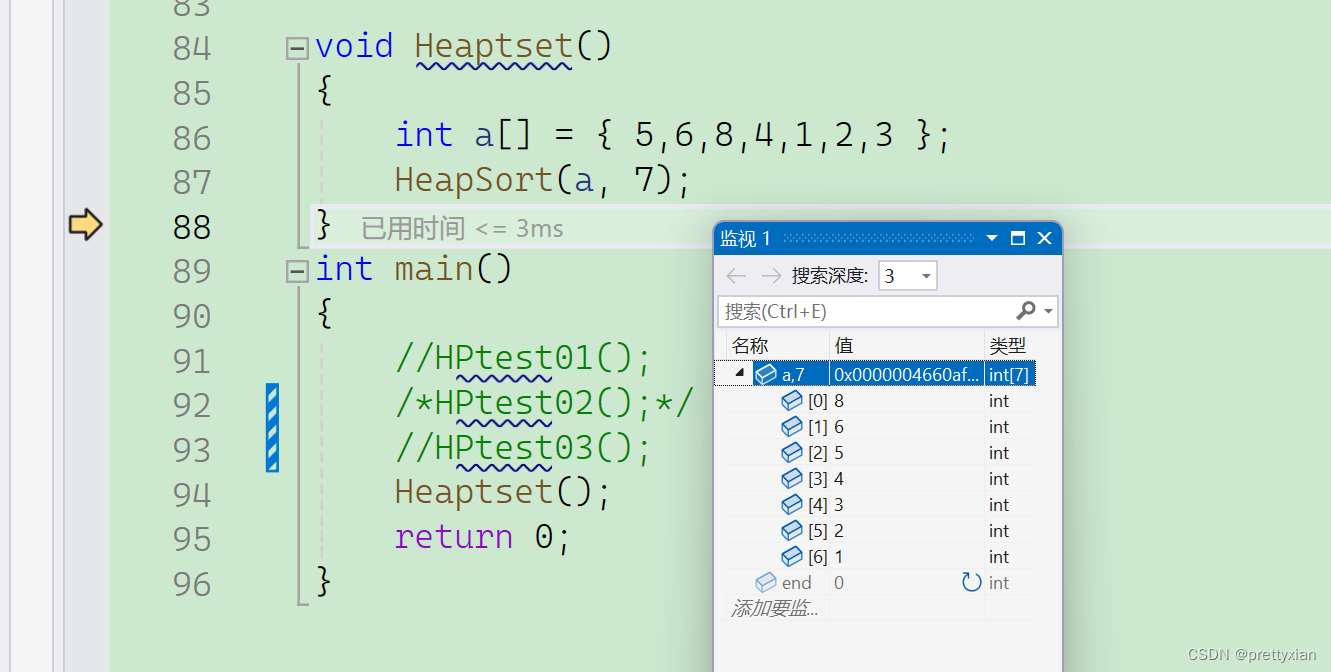
}层序遍历的代码会相对好懂一些。各位也可以进入代码中去研究,想每一步是如何走的。
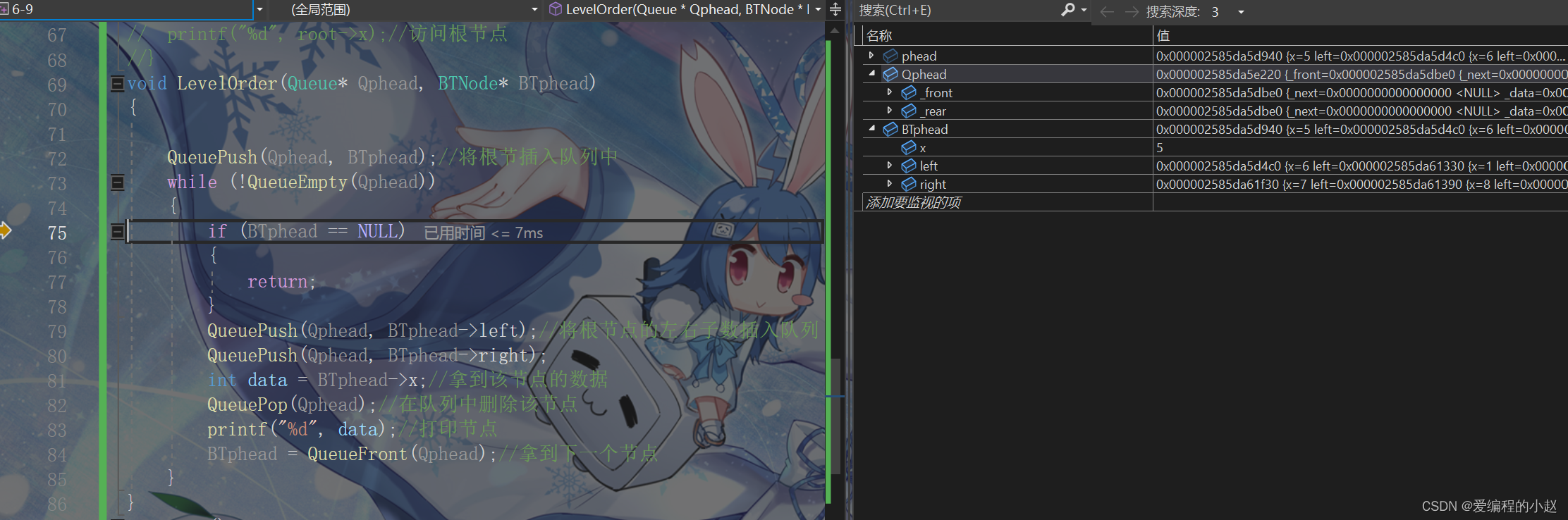
这里用我们的调试功能就能很清晰的知道自己的代码是如何运行的了。
🚈4.二叉树学习的相关建议和方法
二叉树的学习对于整个编程的学习非常重要,它联系着后面的红黑二叉树等相关知识,也联系着我们的重要算法dfs,bfs,在这一阶段,我们要不断地去画递归展开图,才能真正理解透彻这一段代码,小赵在后面也会出一些与其相关的联系题帮助大家去理解。
这里小赵也是从网上找来了相关的动态图片去帮助大家理解。

✍5.结束语
好了小赵今天的分享就到这里了,如果大家有什么不明白的地方可以在小赵的下方留言哦,同时如果小赵的博客中有什么地方不对也希望得到大家的指点,谢谢各位家人们的支持。你们的支持是小赵创作的动力,加油。

如果觉得文章对你有帮助的话,还请点赞,关注,收藏支持小赵,如有不足还请指点,方便小赵及时改正,感谢大家支持!!!