文章目录
- 0. 概述
- 1. 支撑树
- 2. 最小支撑树
- 3. 歧义性
- 4. 蛮力算法
- 5. Prim算法
- 5.1 割与极短跨越边
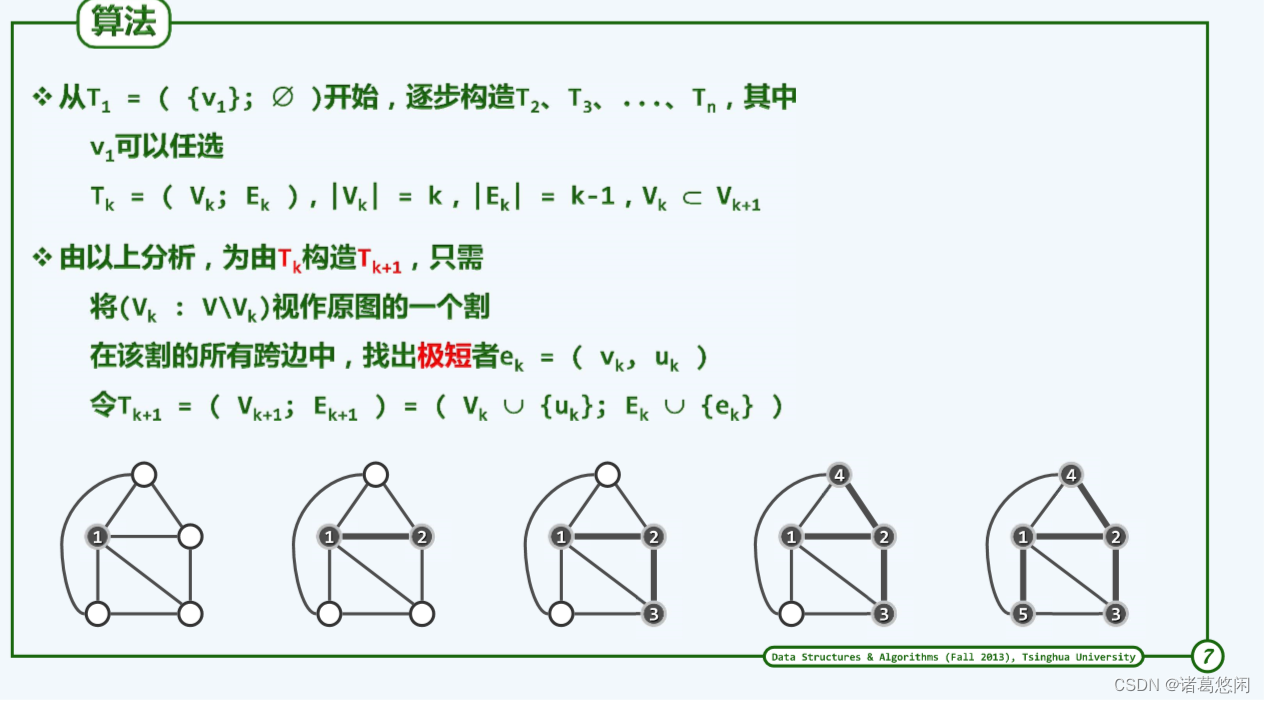
- 5.2 贪心迭代
- 5.3 实例
- 5.4 实现
- 5.5 复杂度
0. 概述
学习下最小支撑树和prim算法。
1. 支撑树
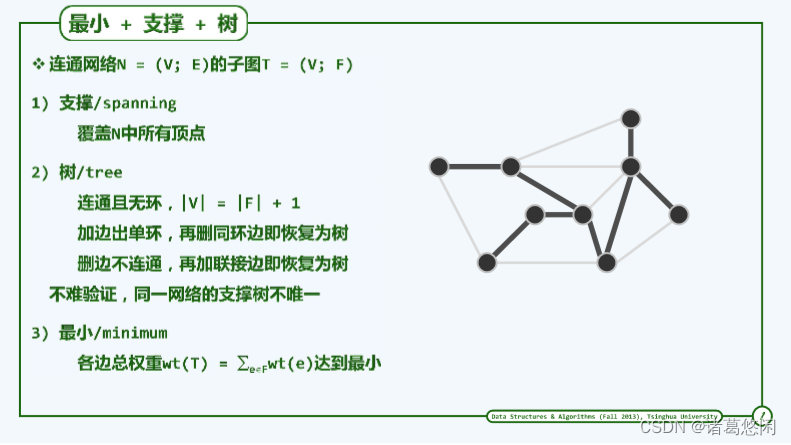
最小的连通图是树。
连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称作G的一棵支撑树或生成树(spanning tree)。
就保留原图中边的数目而言,支撑树既是“禁止环路”前提下的极大子图,也是“保持连通”前提下的最小子图。
确切地,尽管同一幅图可能有多棵支撑树,但由于其中的顶点总数均为n,故其采用的边数也均为n - 1。
2. 最小支撑树
若图G为一带权网络,则每一棵支撑树的成本(cost)即为其所采用各边权重的总和。在G的所有支撑树中,成本最低者称作最小支撑树(minimum spanning tree, MST)。
3. 歧义性
尽管同一带权网络通常都有多棵支撑树,但总数毕竟有限,故必有最低的总体成本。然而,总体成本最低的支撑树却未必唯一。
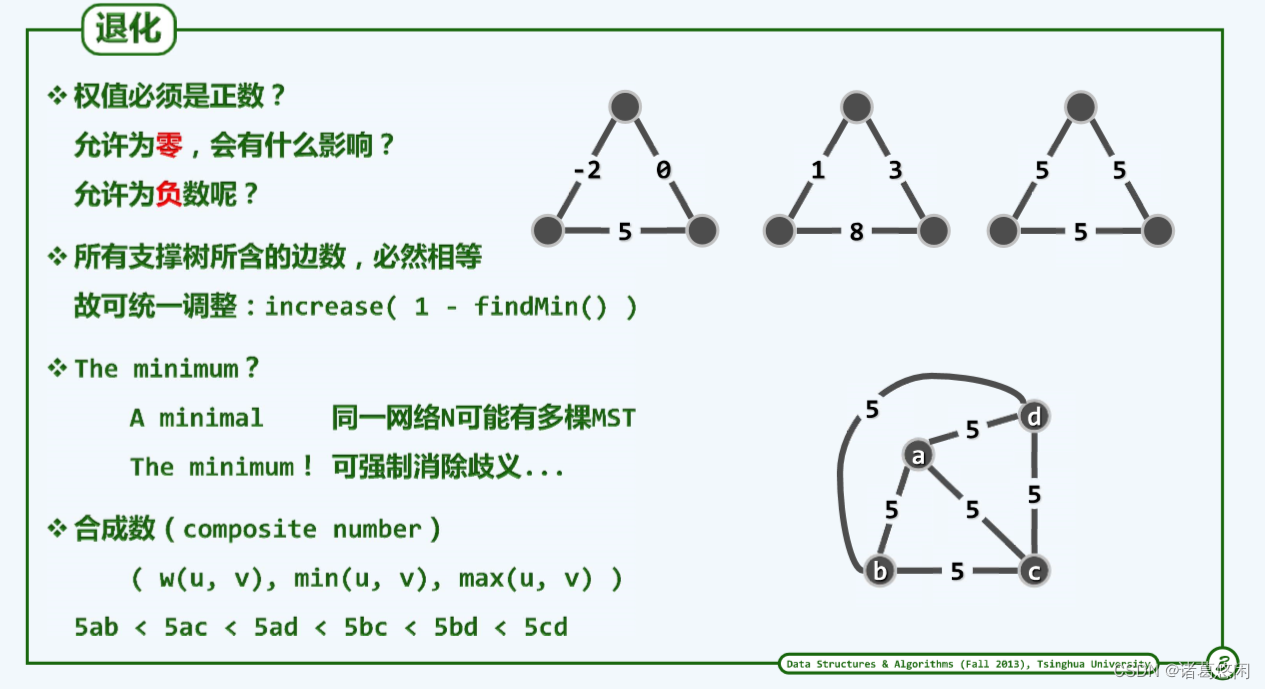
最小支撑树允许有负数,因为它算的是total cast。
若有重边,通过强制附加某种次序即可消除这种歧义性。
4. 蛮力算法
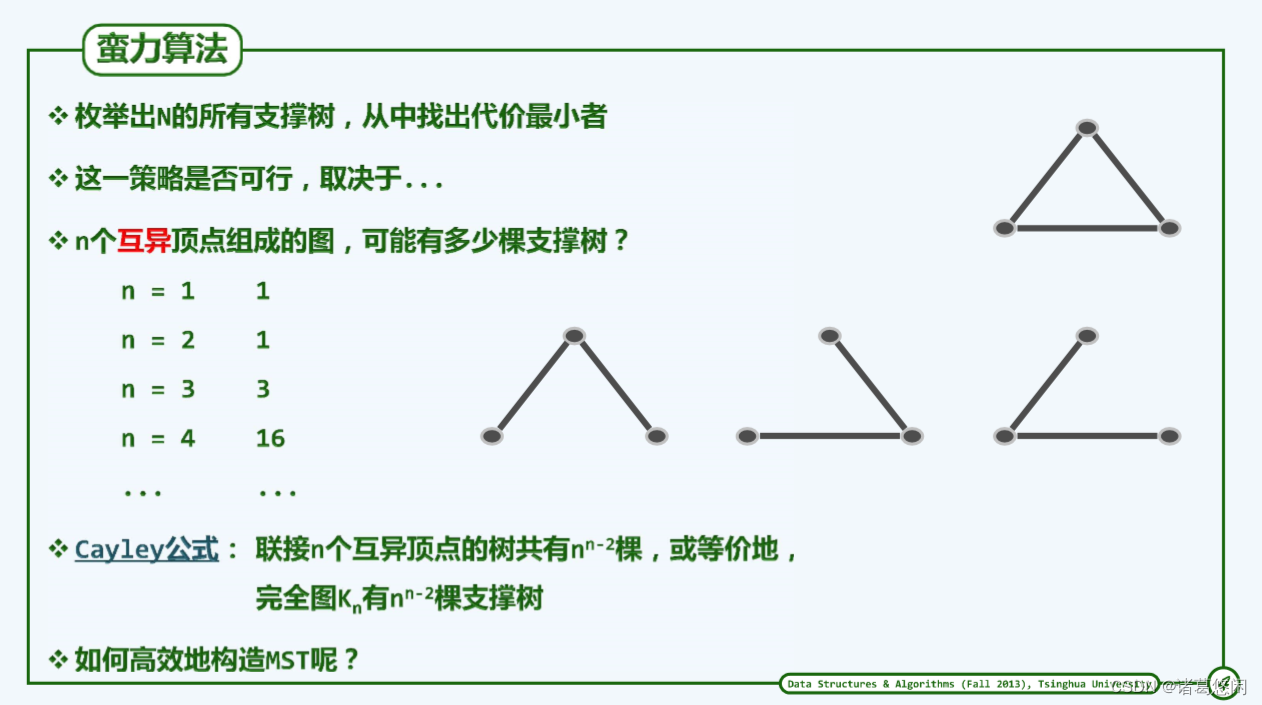
由最小支撑树的定义,可直接导出蛮力算法大致如下:逐一考查G的所有支撑树并统计其成本,从而挑选出其中的最低者。然而根据Cayley公式,由n个互异顶点组成的完全图共有 n n − 2 n^{n-2} nn−2棵支撑树,即便忽略掉构造所有支撑树所需的成本,仅为更新最低成本的记录就需要O( n n − 2 n^{n-2} nn−2)时间。
事实上基于PFS搜索框架,并采用适当的顶点优先级更新策略,即可得出如下高效的最小支撑树构造算法。
5. Prim算法
5.1 割与极短跨越边
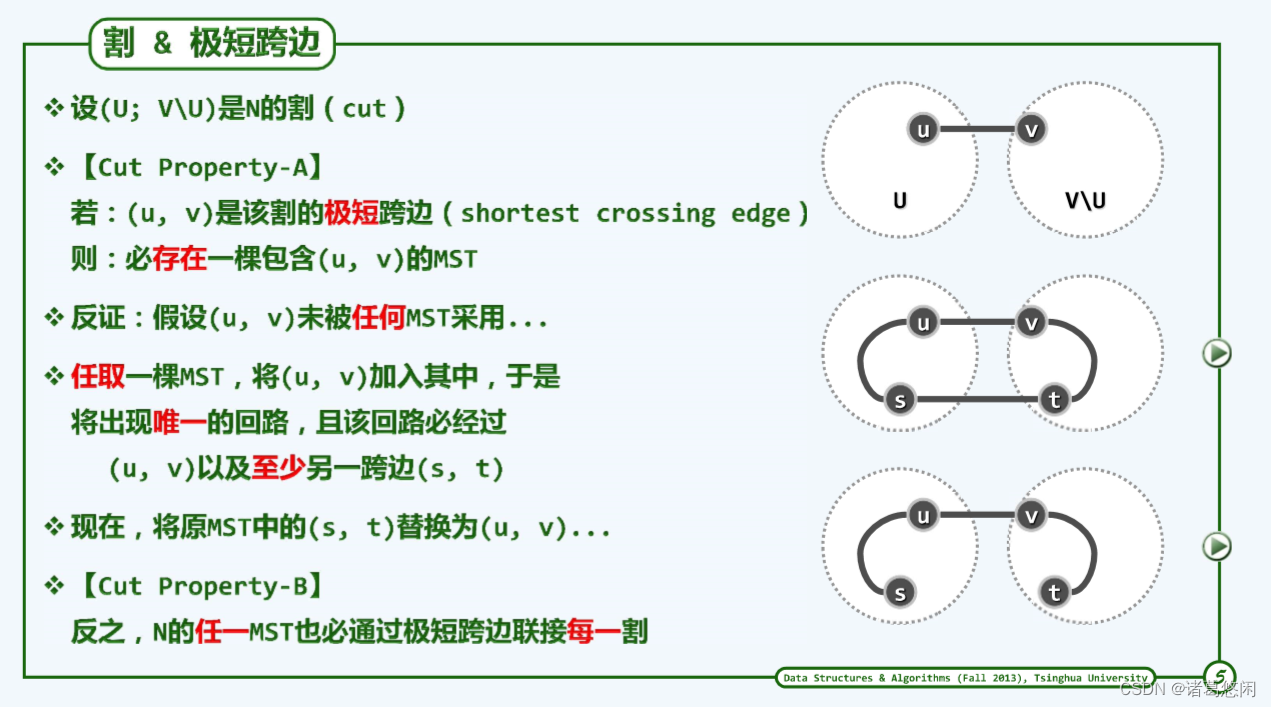
图G = (V; E)中,顶点集V的任一非平凡子集U及其补集V\U都构成G的一个割(cut),记作(U : V\U)。若边uv满足uU且vU,则称作该割的一条跨越边(crossing edge)。因此类边联接于V及其补集之间,故亦形象地称作该割的一座桥(bridge)。
Prim算法的正确性基于以下事实:最小支撑树总是会采用联接每一割的最短跨越边。
5.2 贪心迭代
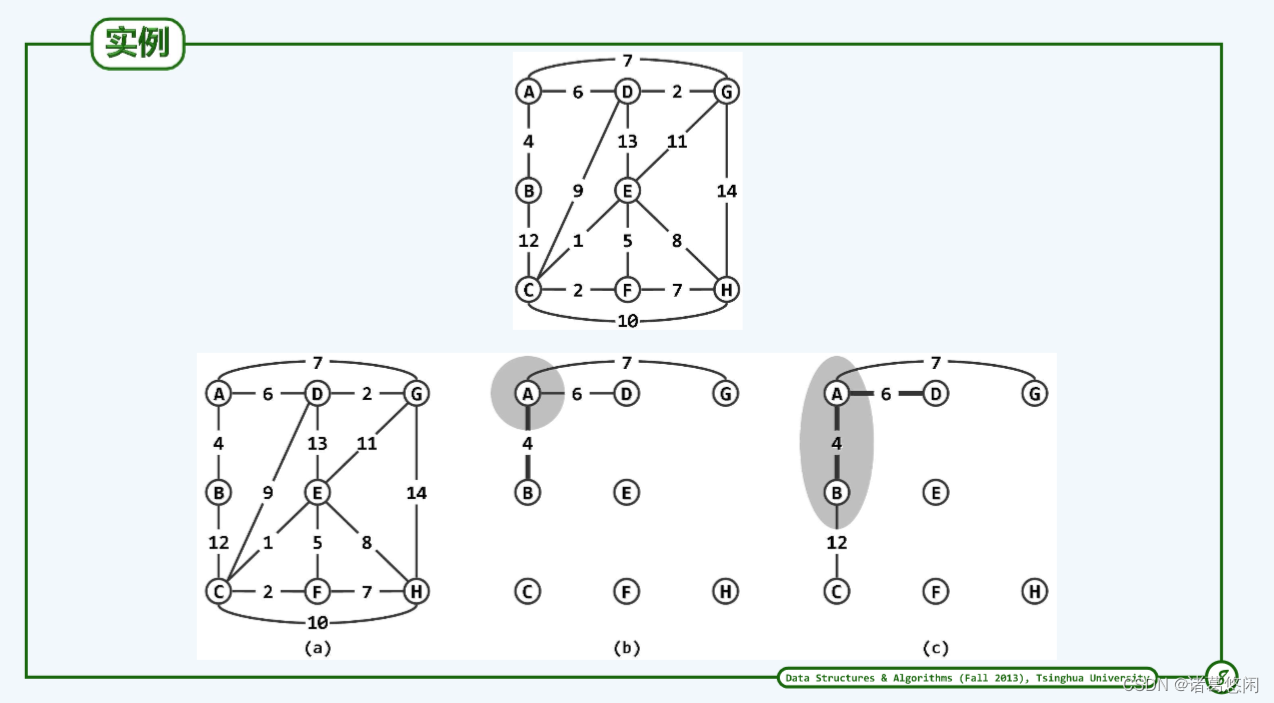
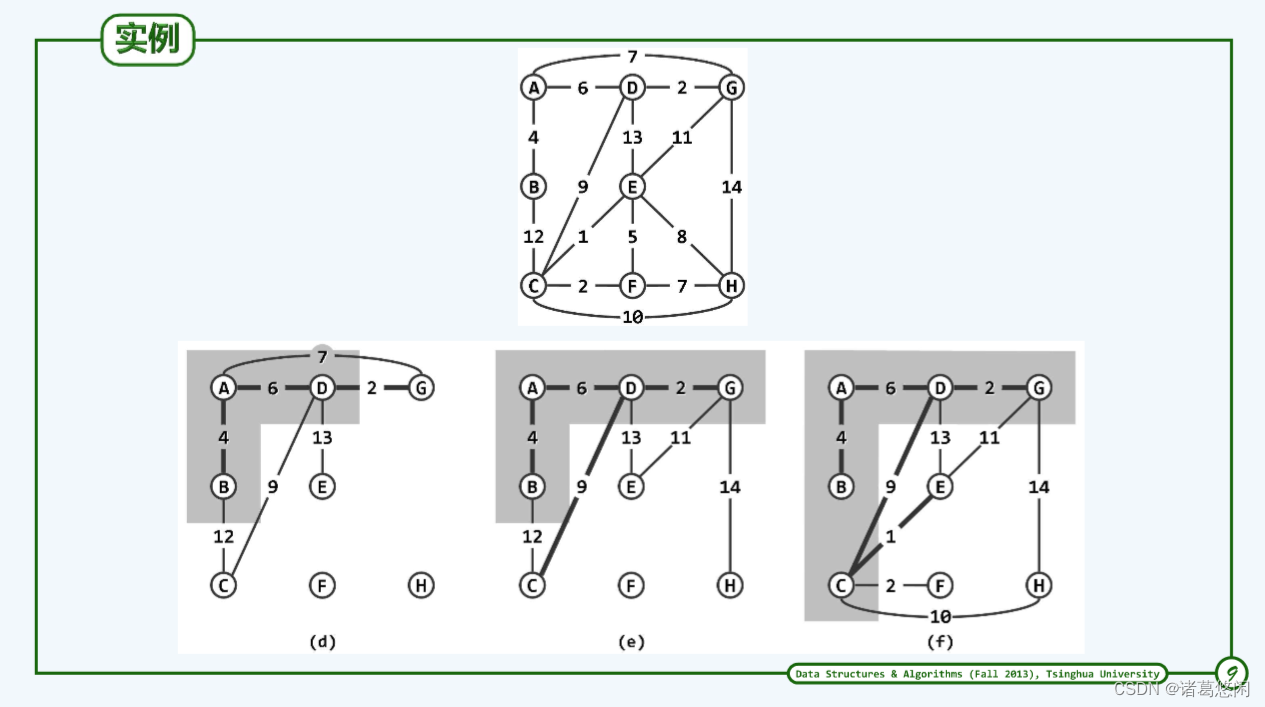
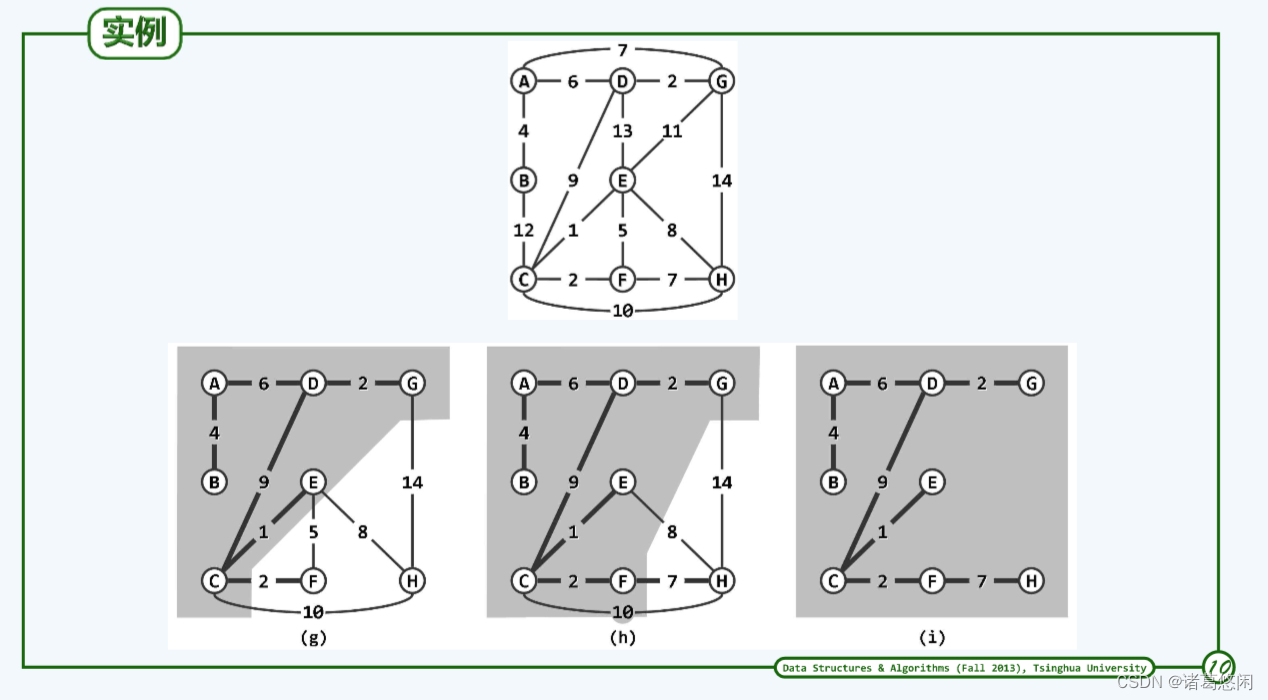
5.3 实例
5.4 实现
这个实现无非就是一个PFS。

这棵子树上的点认为都访问过了,没有访问的点(补集上的点)手上都拥有一个优先级数,这个数就是代表它到子树的距离,这个距离在任何时刻各自都会实现于某个特定的点,每次要做的事就是在树中找到最小的把它拓展进来,接下来再update。

接下来就是为prim算法写一个优先级更新器,实现更新算法。实现流程:
在当前图g中,如果有一个点uk刚刚被扩展进来,加入到这棵树中,对于它的每个尚未被发现的邻居v,按照prim策略做松弛。首先判断下当前的提供的优先级数是否更好,如果当前的优先级数更好便会欣然接受这个。再更新下v的父亲。
5.5 复杂度
目前只是把算法将明白了,数据结构还差的很远,每次查找优先级数还比较慢,以上Prim算法的时间复杂度为O( n 2 n^2 n2)。作为PFS搜索的特例,Prim算法的效率也可借助优先级队列进一步提高。