基础数据结构 -- 堆

1. 简介

堆可以看做是一种特殊的完全二叉树，它满足任意节点的值都大于或小于其子节点的值。

2. 功能

插入元素：插入新元素时，先将元素放至数组末尾，然后通过上浮算法自底向上调整，使堆保持性质。
删除堆顶元素：删除堆顶元素后，将最后一个元素移至堆顶，然后通过下沉算法自顶向下调整，重新满足堆的性质。
建堆过程：从倒数第一个非叶子节点开始，对每个子树进行向下调整，直至整棵树满足堆的性质。

3. 图解

堆结构：

插入元素：

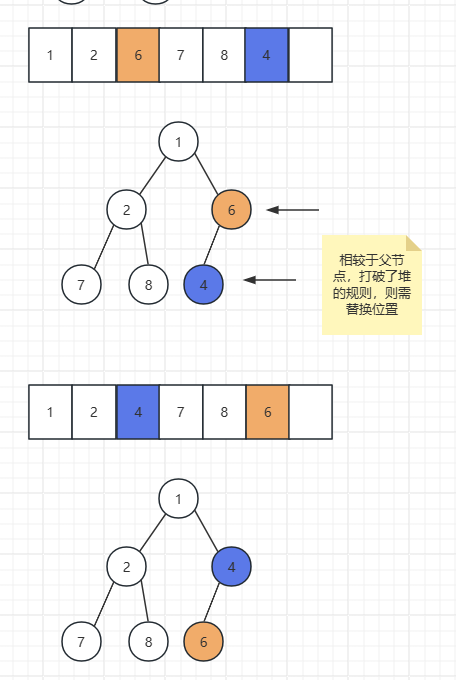
删除堆顶元素：

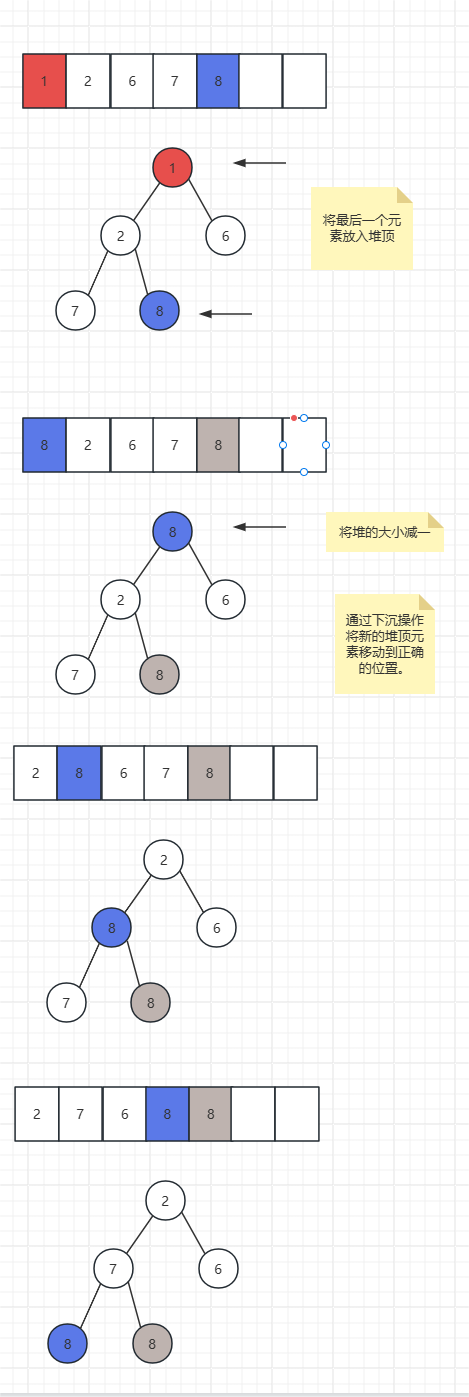
4. 实现

在Java中，堆通常通过数组实现，利用数组的索引来表示节点之间的关系。

具体实现方式如下：

定义一个数组来存储堆的元素。
使用数组下标表示节点的位置，例如根节点的下标为0，左子节点的下标为2 * i + 1，右子节点的下标为2 * i + 2。
在插入元素时，将新元素插入到数组末尾，然后通过上浮操作将其移动到正确的位置。
在删除元素时，将最后一个元素替换到堆顶，然后通过下沉操作将其移动到正确的位置。
在堆排序时，将堆顶元素与最后一个元素交换，然后将堆的大小减一，再通过下沉操作将新的堆顶元素移动到正确的位置。

小根堆代码实现：

public class MinHeap {private int[] data; // 存储堆元素的数组private int size; // 堆的大小public MinHeap(int capacity) {data = new int[capacity];size = 0;}// 返回堆的大小public int getSize() {return size;}// 返回堆是否为空public boolean isEmpty() {return size == 0;}// 返回父节点的索引private int parent(int index) {return (index - 1) / 2;}// 返回左子节点的索引private int leftChild(int index) {return 2 * index + 1;}// 返回右子节点的索引private int rightChild(int index) {return 2 * index + 2;}// 上浮操作private void siftUp(int index) {while (index > 0 && data[parent(index)] > data[index]) {swap(parent(index), index);index = parent(index);}}// 下沉操作private void siftDown(int index) {while (leftChild(index) < size) {int minIndex = leftChild(index);if (rightChild(index) < size && data[rightChild(index)] < data[minIndex]) {minIndex = rightChild(index);}if (data[index] <= data[minIndex]) {break;}swap(index, minIndex);index = minIndex;}}// 交换两个元素的位置private void swap(int i, int j) {int temp = data[i];data[i] = data[j];data[j] = temp;}// 向堆中插入元素public void insert(int value) {if (size == data.length) {throw new IllegalStateException("Heap is full");}data[size] = value;siftUp(size);size++;}// 从堆中删除最小元素（即堆顶元素）public int extractMin() {if (isEmpty()) {throw new IllegalStateException("Heap is empty");}int minValue = data[0];data[0] = data[size - 1];size--;siftDown(0);return minValue;}
}

也有一个偷懒的办法，我们可以通过 Java 内置的 PriorityQueue 类来实现最小堆。通过调用add() 方法可以向堆中插入元素，而通过调用 poll() 方法可以从堆中删除最小元素（即堆顶元素）。

需要注意的是，PriorityQueue 默认实现的是最小堆，如果需要实现最大堆，可以通过传递自定义比较器来实现。例如，使用 PriorityQueue<Integer>(Conleections.reverseOrder()) 来创建一个最大堆。

public class HeapTest {public static void main(String[] args) {// 创建一个最小堆PriorityQueue<Integer> minHeap = new PriorityQueue<>();// 向堆中插入元素minHeap.add(5);minHeap.add(2);minHeap.add(8);minHeap.add(1);minHeap.add(3);System.out.println("最小堆的元素： " + minHeap); // 输出： [1, 2, 8, 5, 3]// 从堆中删除最小元素（堆顶元素）int minElement = minHeap.poll();System.out.println("被删除的最小元素： " + minElement); // 输出： 1System.out.println("删除最小元素后的最小堆： " + minHeap); // 输出： [2, 3, 8, 5]}
}

7. 应用场景

堆排序：利用最大堆或最小堆的性质，可以进行高效的排序操作。堆排序是一种时间复杂度为O(n log n)的排序算法，它通过建堆和反复删除堆顶元素进行排序。
中位数查询：使用最大堆和最小堆可以在O(log n)的时间内查询一组数据的中位数，这对于实时数据分析等领域非常重要。
Top K问题：对于一个数据流，需要在其中找到前K大或前K小的元素，可以使用堆来实现。维护一个大小为K的堆，遍历数组，从数组中取出数据与堆顶元素比较，如果比堆顶元素大，则将堆顶元素删除，并将这个元素插入到堆中；如果比堆顶元素小，则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前K大数据了。