穷举vs暴搜vs深搜vs回溯vs剪枝
- 1.全排列
- 2.子集

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
管他什么深搜、回溯还是剪枝,画出决策树就完事了~~~
1.全排列
题目链接:46. 全排列
题目描述:

算法原理:
其实这道题本身是一个穷举(枚举)的题,3个数你可以三层for循环,但是如果10个数,100个数呢?对于数多的显然不合适!此时我们就需要借助递归把所有情况都枚举出来。
解决回溯的步骤:
- 画出决策树,越详细越好!
- 设计代码
全局变量
dfs函数
细节问题
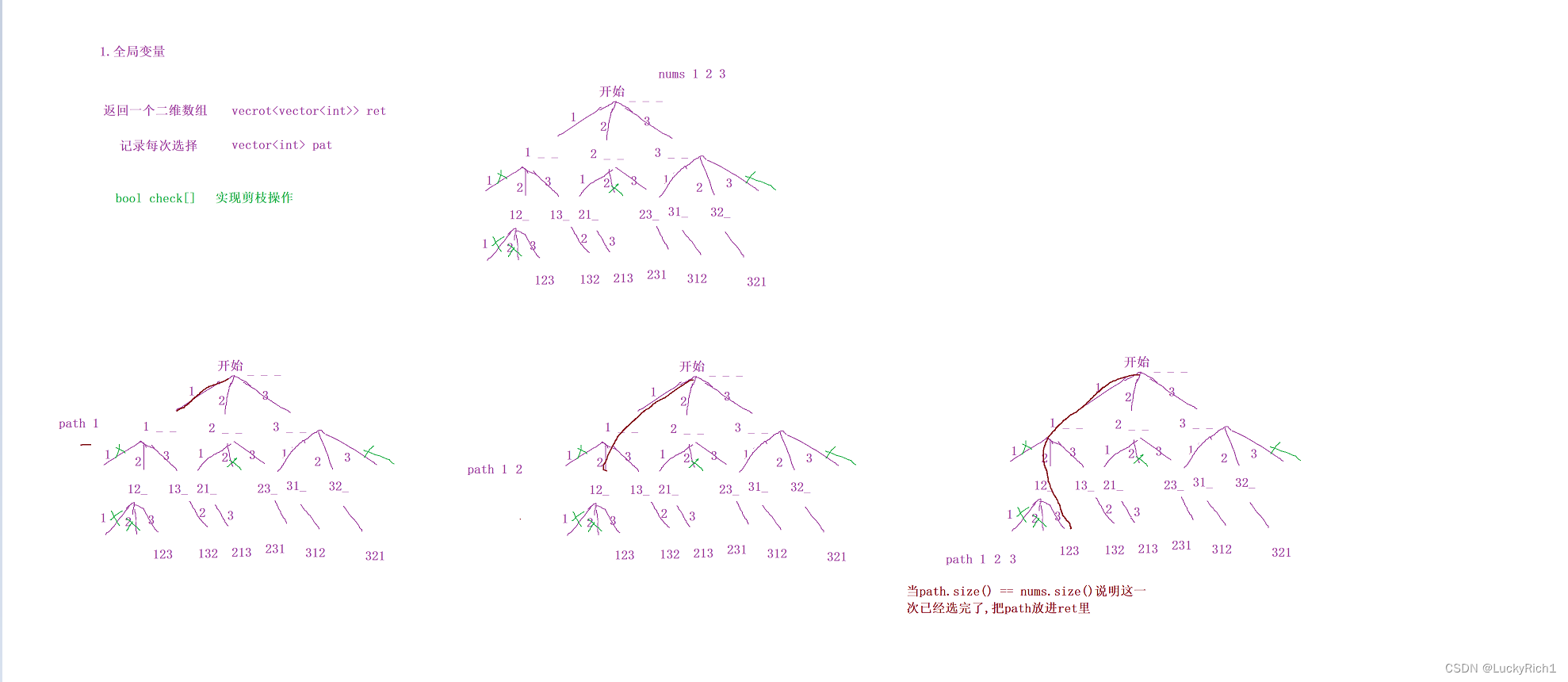
1.画出决策树
就是在暴力枚举这道题过程中如何不重不漏的把所有情况枚举到,就是把自己的想想法按照树的样子画下来。
第一次选择可以直接选123中任何一个,接下来每次选择都是从123中选。但是此时你会发现比如第一次选1,下一次还选1就会有重复的情况,因此这个1我们是要把它剪掉的,不考虑有1的情况。第二次选择假设选择的是2,在往下选择就还是有123,但是此时剪掉的应该更多,12不能选,只能选3,所有最终这条分支就是123,同理其他也是这样选出。

决策树画的越详细越好,就是把每一步都画出来,这样你就会发现每一个节点干的事情都是一样的,都是枚举整个数组。无非就是一些分支被我们剪掉。当一直在干同一件事情的时候我们决策树就画成功了,因为可以改成递归的代码。
2.设计代码
1.全局变量
全局变量就看这个递归需要什么东西和以及最终要返回什么东西。
全局变量的使用仁者见仁智者见智,也可以把全局变量换成参数在递归函数中传递。看个人选择,不过还是建议使用全局变量!
首先来递归要返回的二维数组,再来一个把每次选择都要记录的path。
当path.size() == nums.size() 说明已经找到一个符合的组合,此时把path放到ret里,然后回溯 ,注意要 恢复现场。在说这个之前我们要说一说这个剪枝的事情。

剪枝怎么解决?就是如果避免下一次选择重复的数字。
此时我们也需要一个数组,弄一个bool 类型的数组。来判断一下该条路径下的数是否已经被使用过了。bool数组中记录nums数组中的数字是否已经被使用过。
check[0] 对应 1, check[1] 对应 2 , check[2] 对应3,check初始化都为false,只有对应数字被使用了 check[i]=true,说明这个数字已经被使用过了,下一次就不要选这个数字了。
2.dfs函数
仅需关心,某一个节点在干什么事情。
3.细节问题
回溯
当我要回去的时候,需要把这个3干掉,就是向上回去把path最后一个元素干掉,但是别忘记了check也是一个全局的, 你用3的时候会把check对应位置置为true,那你向上返回这个3你都不用了,是不是要把3复原啊。
- 干掉 path 最后一个元素
- 修改 check 数组
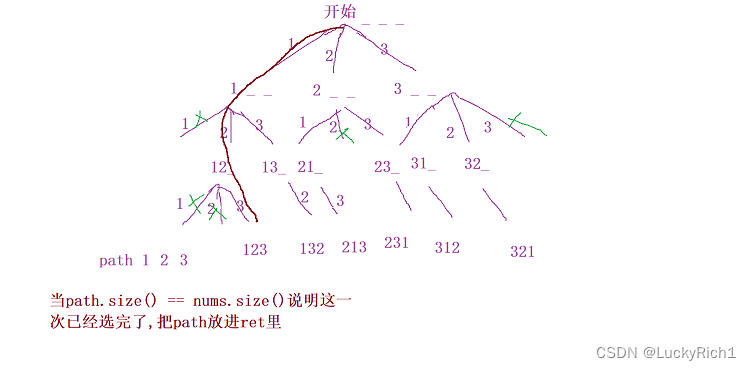
剪枝
这里前面说过。
递归出口
遇到叶子节点的时候,直接添加结果。不用在到空了。
这样的题一定是决策树画出来是最重要的,第二步设计代码你想到哪一点写那一点都可以。
class Solution {vector<vector<int>> ret;vector<int> path;bool check[7]={false};
public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size() == nums.size()){ret.push_back(path);//返回之前可以 回溯 --> 恢复现场return;}for(int i=0;i<nums.size();++i){//剪枝if(check[i] == false){path.push_back(nums[i]);check[i]=true;dfs(nums);//返回之后也可以 回溯 ---> 恢复现场 ,建立返回之后check[i]=false;path.pop_back(); }}}
};
注意一定是决策树越详细后面代码设计越轻松,代码设计考虑一下全局变量、dfs函数、细节问题。
2.子集
题目链接:78. 子集
题目描述:

算法原理:
这里我们采用两种策略来解决这个问题,虽然是两种策略,但都是深搜,所以我们的思考方式是一样的。
解法一:
- 画出决策树
- 设计代码
全局变量
dfs
细节:回溯、剪枝、递归出口
首先画决策树,我们想想如何能够把所有子集不重不漏全部枚举出来。我们从子集定义出发,子集是这个数组里面选or不选某些数形成新的集合就是它的子集。因此我们就单独盯着数组中每个数字考虑选or不选来画出我们的决策树。
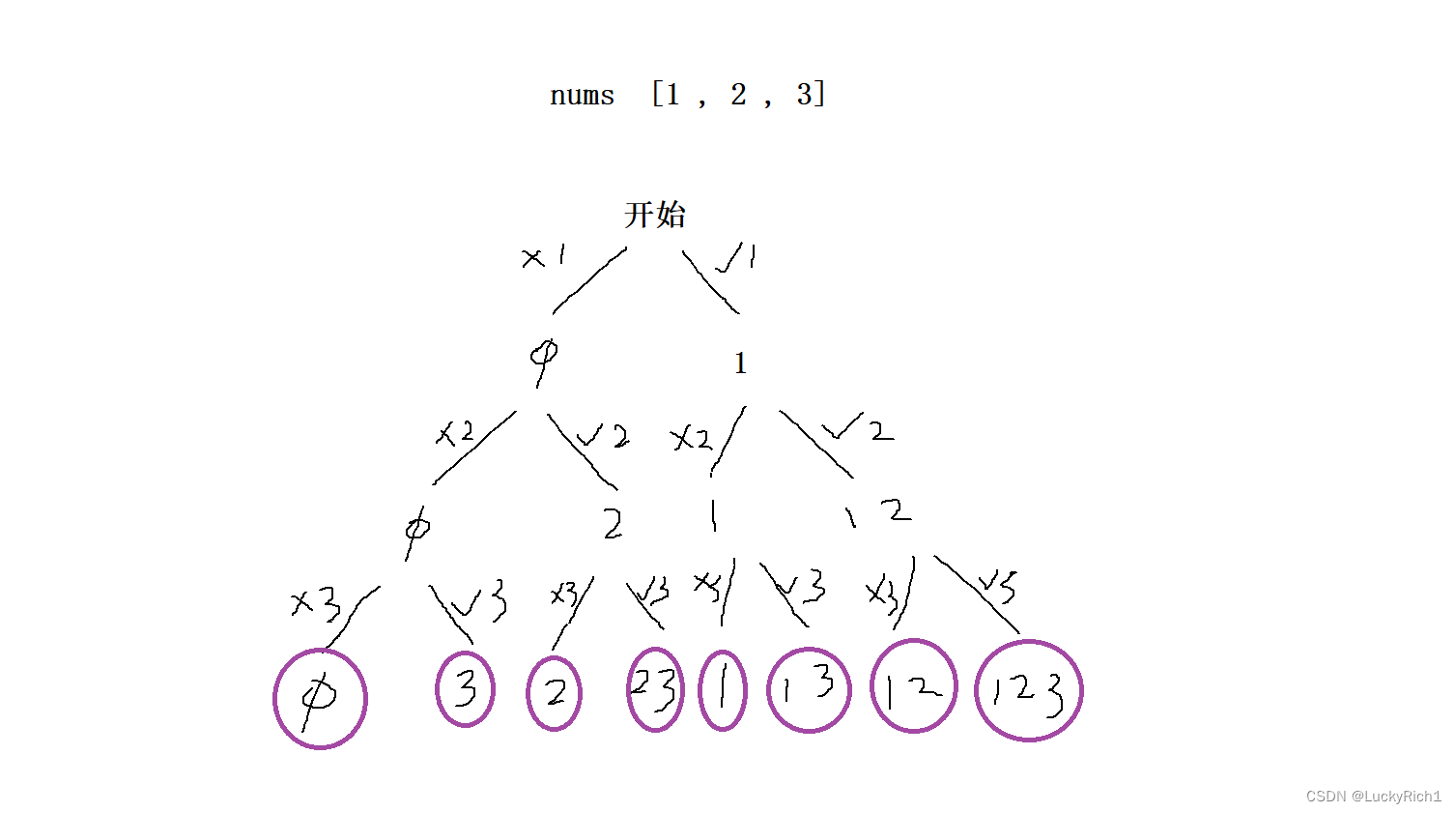
此时所有叶子节点就是数组所有不重复的子集。
现在我们仅需把这颗决策树转换成代码就可以了。之前的题无非就是直接把树画好给我们了,现在是要我们自己画一颗树。
既然叶子节点是我们的结果,因此我们需要两个全局变量,一个二维数组ret,一个一维数组path,path把每次选or不选路径记录下来,然后ret把path记录下来。这道题我们并不需要剪枝。
dfs函数我们就盯着某一个位置在干什么。比如绿圈的位置,因为上面已经选过了,所以要需要考虑这一次的数选or不选,所以dfs不仅要这个nums,还要告诉我你当前选到了那个位置,dfs(nums,pos)
选就加入到path里,然后dfs(nums,pos+1)下一层
不选直接 dfs(nums,pos+1)下一层
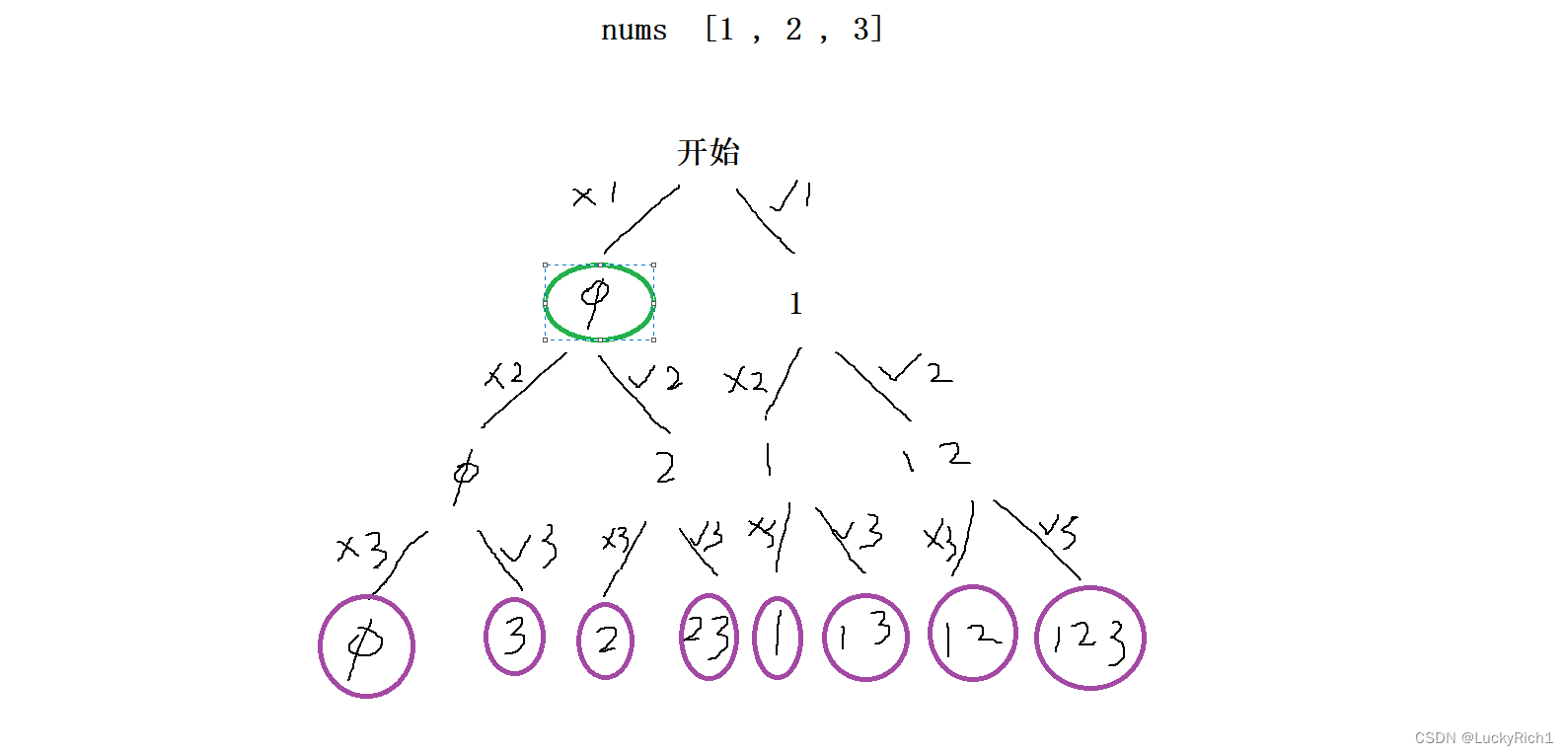
细节问题:回溯要恢复现场,因此我们在选的这条路径在递归返回之后把path最后一个位置pop掉,剪枝我们这里没有。递归出口当pos==nums.size()的时候,把path放到ret里,然后返回即可。
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos == nums.size()){ret.push_back(path);return;}// 选path.push_back(nums[pos]);dfs(nums,pos+1);path.pop_back(); // 恢复现场// 不选dfs(nums,pos+1);}
};
解法二:
也是上面一样的步骤,
- 画出决策树
- 设计代码
全局变量
dfs
细节:回溯、剪枝、递归出口
这里我们换一种思考方式,当我们选的子集是没有元素、只有一个元素、只有两个元素、只有三个元素等等。前面的是盯着某一个数选or不选,现在我们直接看看最终要的子集要么没有,要么一个元素,要么两个元素,要么三个元素等等,从小到大去选。并且每次是从这个被选的数的后面再次选。并且每一个节点都是我们想要的结果。

你会发现我们这种解法比上面少了很多没有必要的情况。
全局变量还是上面那两个,dfs函数 从当前节点位置开始向后枚举,所以也要知道当前位置 dfs(nums,pos)。for(int i=pos;i<nums.size();++i) 把路径上的节点放入path,然后递归到下一层dfs(nums,pos+1),当递归返回收把path最后一个位置pop掉。 回溯也要恢复现场,把path最后一个位置pop掉,这里我们不用剪枝,递归出口,每次进入递归函数后先把path先放到ret里。然后也不需要出口,循环条件不满足就出去了。
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){ret.push_back(path);for(int i=pos;i<nums.size();++i){path.push_back(nums[i]);dfs(nums,i+1);path.pop_back(); // 恢复现场}}
};