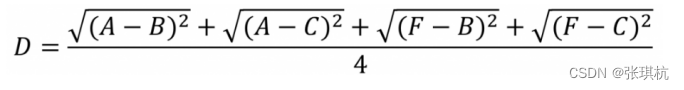1.有监督学习与无监督学习
有监督:在训练集中给的数据中有X和Y,根据这些数据训练出一组参数对预测集进行预测
无监督:在训练集中给的数据只有X没有Y,根据X数据找相似度参数来对预测集进行预测
2.数据间的相似度
2.1距离相似度:
每一条数据可以理解为一个n维空间中的点,可以根据点点之间的相似度来评价数据间的相似度
欧氏距离:欧式距离就是两个点之间的直线距离
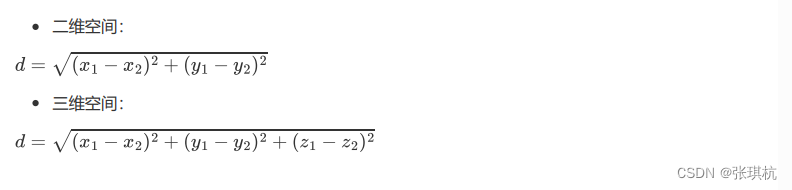
曼哈顿距离:以二维空间为例,这种距离是计算两点之间的直角边距离,相当于城市中出租汽车沿城 市街道拐直角前进而不能走两点连接间的最短距离。
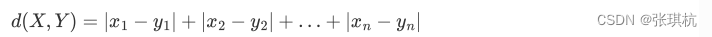
闵可夫斯基距离:p=1的时候就是曼哈顿距离,p=2的时候就是欧式距离,P = 无穷,切比雪夫距离 ,哪个维度差值最大就是哪个差值作为距离。根据极限的思想p无穷大的时候x-y的值小的肯定远小于x-y大的值,那么就是最大的一个x-y占主要距离
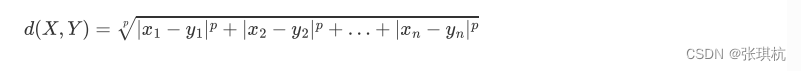
余弦距离:高中都学过
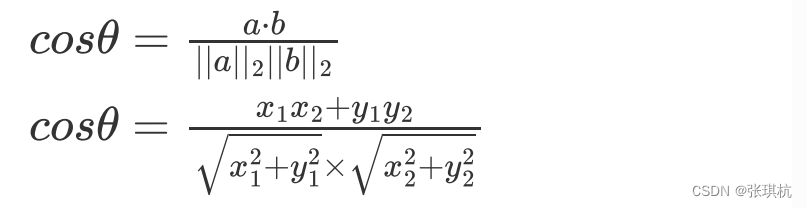
3.Kmeans算法
1.聚类原理:
将N个样本映射到K个簇中,每个簇至少有一个样本,先给定K个划分,迭代样本与簇的隶属关系,每次都比前一次好一些,迭代若干次就能得到比较好的结果。也就是先给你一堆球,但是不告诉你这些球的颜色,然后你自己去分,分成几种颜色是比较好的结果
2.Kmeans算法原理:
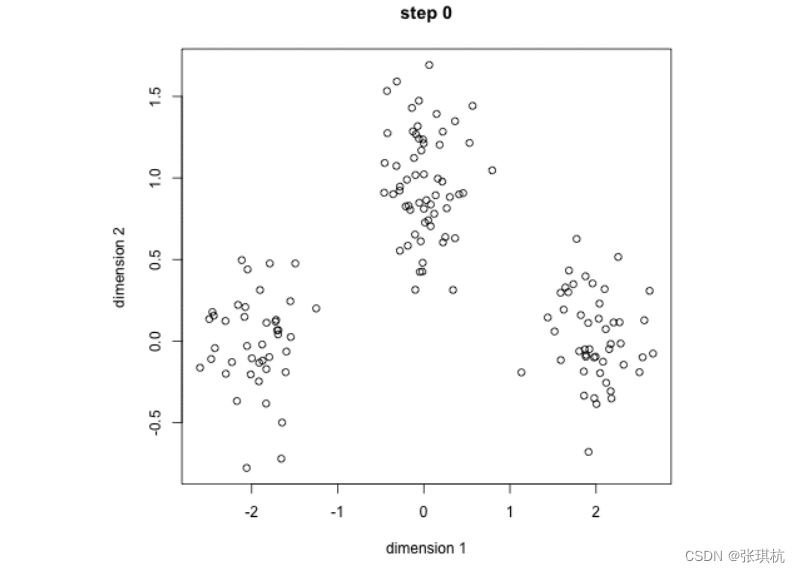
1.先随机生成k个初始的簇中心,也就是先随机挑几个球
2.逐个计算每个样本到这些簇中心的距离,将样本归属到距离最小的那个簇中心的簇中,也就是计算其他球到这些呗选择的球的距离,离那个球近就归那个球
3.每个簇内部计算平均值,跟新簇中心。也就是第二步选出来的k个簇,每一个簇中的每个球都计算它到其他球的距离的平均值,然后选择最小的一个球当作簇中心
一直迭代更新簇中心,直到不再改变 ,最后分好的k个簇就是分k种颜色的球的比较好的结果(这里只是局部最优,如果要全局最优需要迭代k的值,也就是要找到分多少种颜色才能让这些球每种颜色距离最远)
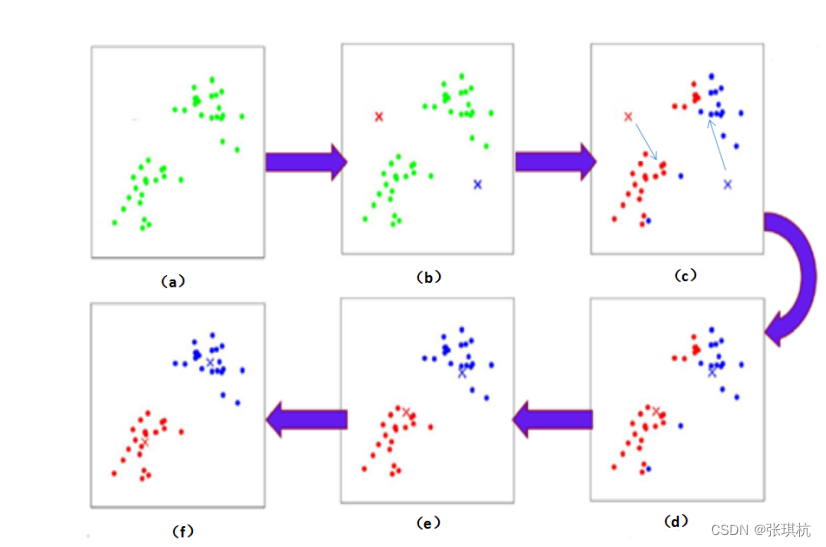
KMeans的优点:简单。缺点:对异常值敏感,对初始值敏感,对某些分布聚类效果不好。
4.Kmeans损失函数:

5.kmeans执行过程
6.Kmeans聚类算法k值的选择
样本点的轮廓系数:
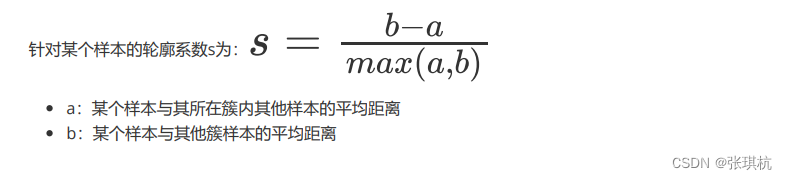
按照公式每一个样本点都有一个轮廓系数,那么该样本的总的轮廓系数为:
也就是每一个样本点的轮廓系数的平均值。而聚类总的轮廓系数SC是该聚类是否合理,有效的度量
所以,我们在迭代k值的时候不用盲目的去迭代了,而是要看这个聚类总的轮廓系数SC。我们将k从2开始迭代,一直迭代到SC沿下降趋势的时候就可以了,找到SC最大的时候的k的值,就是结果了
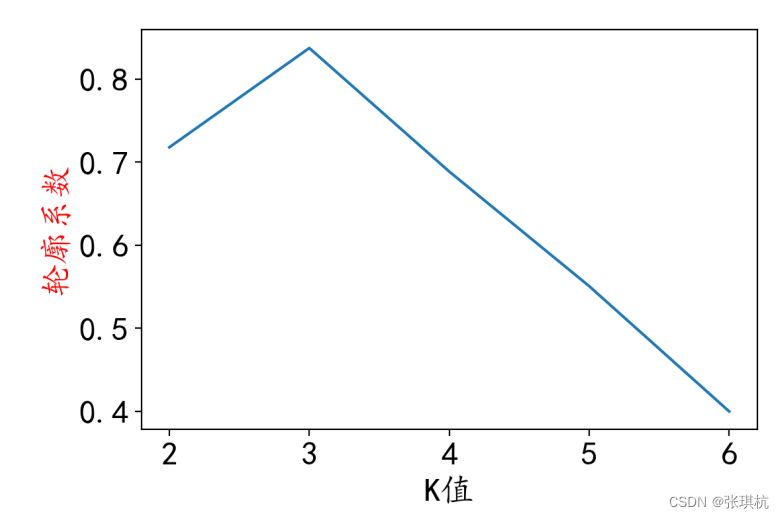
4.DBSCAN算法
1.算法介绍:
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类 方法)是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇,并在具有噪声的空间 数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
2.DBSCAN算法原理
1.先随机找一个点,通过欧式距离计算附近点的距离
2.如果距离小于阈值(自己定义的eps)就属于同一类
3.每一次迭代还有一个阈值,min_samples,也就是每次迭代最少要找到的同类数
4.将第二步找到的同类点进行2,3步迭代
5.当所有点都不满足第三步时,重新从第一步进行迭代,直到所有样本结束
动画详情地址:Visualizing DBSCAN Clustering (naftaliharris.com)
参数详细:
参数一eps: DBSCAN算法参数,即我们的eps邻域的距离阈值,和样本距离超过eps的样本点不在eps邻域内。默认 值是0.5.一般需要通过在多组值里面选择一个合适的阈值。eps过大,则更多的点会落在核心对象的eps 邻域,此时我们的类别数可能会减少, 本来不应该是一类的样本也会被划为一类。反之则类别数可能会 增大,本来是一类的样本却被划分开。
参数二min_samples: DBSCAN算法参数,即样本点要成为核心对象所需要的eps邻域的样本数阈值。默认值是5。一般需要通 过在多组值里面选择一个合适的阈值。通常和eps一起调参。在eps一定的情况下,min_samples过大, 则核心对象会过少,此时簇内部分本来是一类的样本可能会被标为噪音点,类别数也会变多。反之 min_samples过小的话,则会产生大量的核心对象,可能会导致类别数过少。
参数与三metrics:点和点之间的距离计算公式,一般为欧式距离,当然也可以是曼哈顿距离等等
4.分层聚类:
1.算法介绍:
分层聚类输出层次结构,这种结构比平面聚类返回的非结构化聚类集更具信息性。 分层聚类法(hierarchical cluster method)一译“系统聚类法”。聚类分析的一种方法。其做法是开始时 把每个样品作为一类,然后把最靠近的样品(即距离最小的群品)首先聚为小类,再将已聚合的小类按 其类间距离再合并,不断继续下去,最后把一切子类都聚合到一个大类。
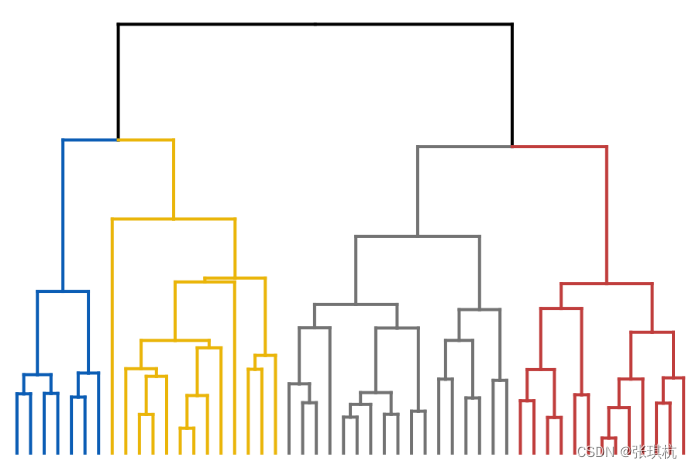
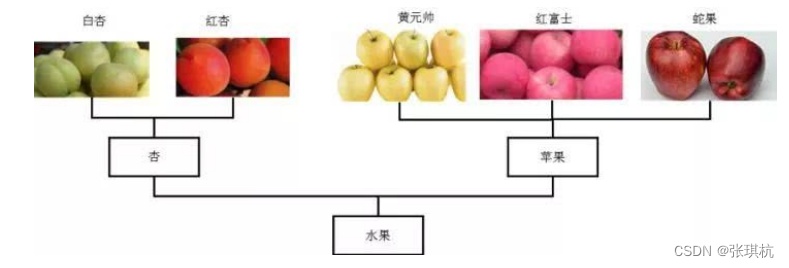
2.算法原理
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵 有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节 点。创建聚类树有自下而上合并和自上而下分裂两种方法。 我们着重看一下自底向上的合并算法:
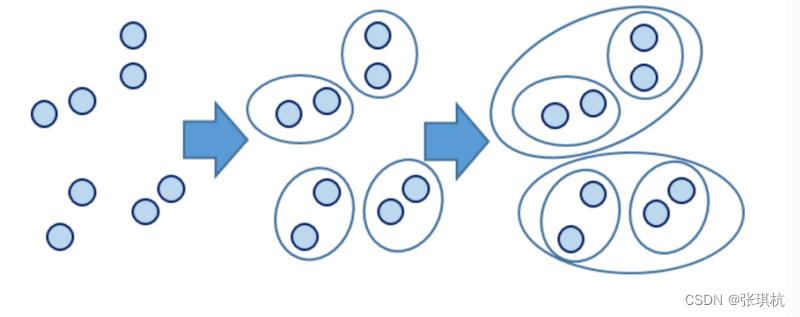
两个组合数据点间的距离:
第一种:Single Linkage 方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这 种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距 离较近而组合在一起。也就是两种球,我们以这两种球中距离最短的两个球的距离当作这两种球的距离
第二种:Complete Linkage 的计算方法与Single Linkage相反,将两个组合数据点中距离最远的两个数 据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相 反,两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。也就是两种球,我们以这两种球中距离最远的两个球的距离当作这两种球的距离
第三种:Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距 离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两 种方法更合理。 我们使用Average Linkage计算组合数据点间的距离。下面是计算组合数据点(A,F)到(B,C)的距 离,这里分别计算了(A,F)和(B,C)两两间距离的均值。也就是两种球,我们以这两种球中所有球的距离的平均值当作这两种球的距离