分而治之
分治法所能解决的问题一般具有以下几个特征:
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的子问题,即该问题具有最优子结构性质
3) 利用该问题分解出的子问题的解可以合并为该问题的解
4) 该问题所分解出的各个子问题是相互独立的, 即子问题之间不包含公共的子问题
第一条特征是绝大多数问题都可以满足的, 因为问题的计算复杂性一般是随着问题规模的增加而增加.
第二条特征是应用分治法的前提它也是大多数问题可以满足的, 此特征反映了递归思想的应用.
第三条特征是关键, 能否利用分治法完全取决于问题是否具有第三条特征, 如果具备了第一条和第二条特征, 而不具备第三条特征, 则可以考虑用贪心法或动态规划法.
第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作, 重复地解公共的子问题, 此时虽然可用分治法, 但一般用动态规划法较好.
快速排序
题目1: 颜色分类

此题和双指针算法中的 题目1: 移动零 很类似, 不过是多了一个指针去维护一块区域:
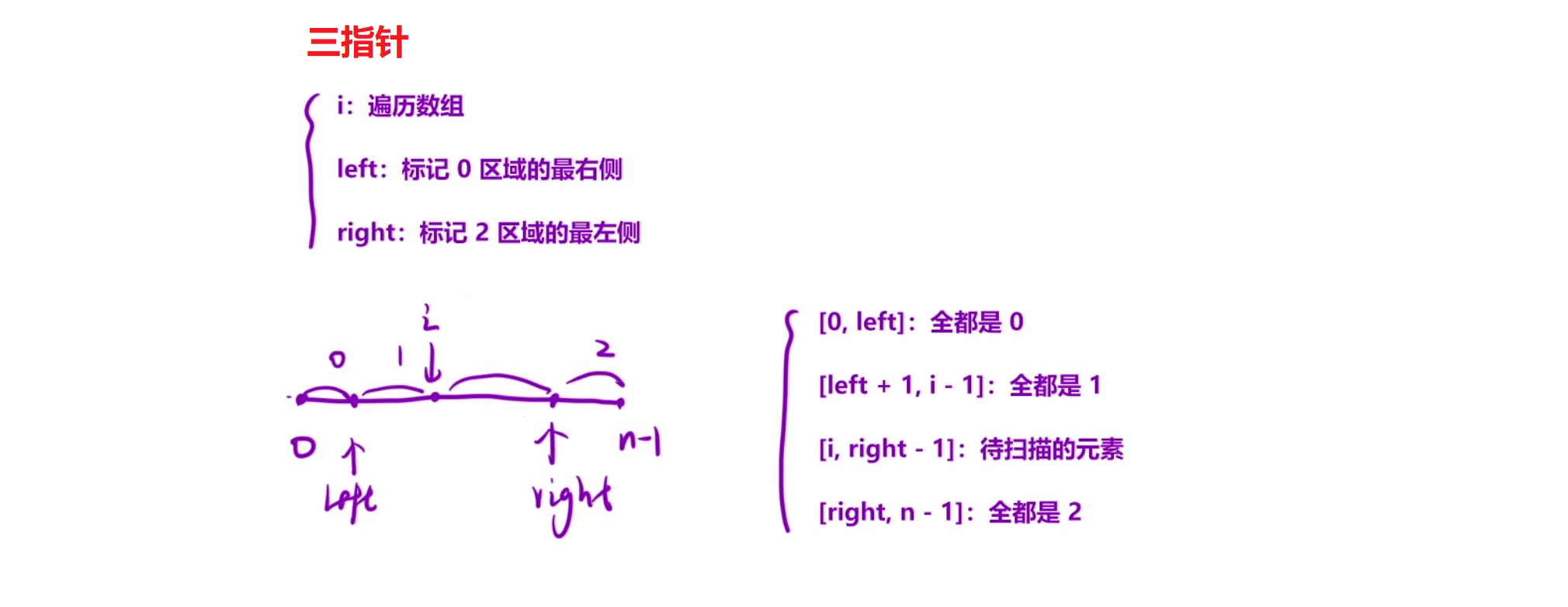
将区域划分为[0,left][left+1, cur][cur+1, right-1][right, n-1] 分别对应0区域, 1区域, 未判断区域, 2区域.
当 i 遍历时遇到 0 则交换 left+1位置和 i 位置的值, 因为left + 1位置的值:
如果[left+1, i]区间(值为1)长度大于0, 则 left+1 位置一定是1, 如果区间长度为0, 则 left+1 一定是0, 自己交换自己, 只是把值为0的区间更新了, 值为1的区间长度依然是0. 注意cur要++, 因为此时cur的值要么是0要么是1, 如果是0且cur不++则会陷入死循环.
当 i 遍历遇到1, 直接跳过
当 i 遍历遇到 2, 交换 right-1 和 i 位置的值, cur不要++
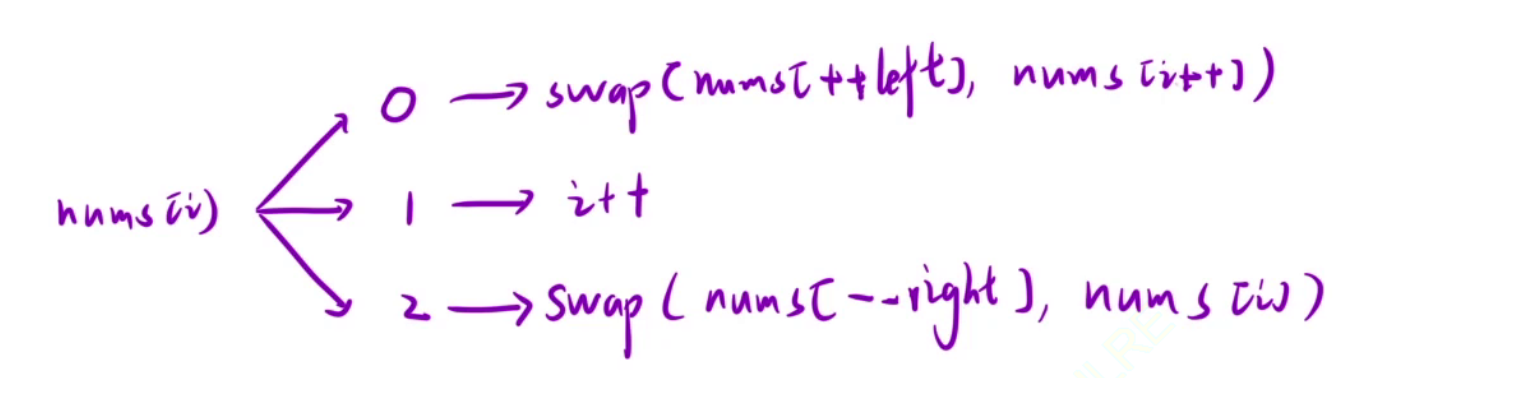
class Solution {
public:void sortColors(vector<int>& nums) {int cur = 0, left = -1, right = nums.size();int n = nums.size();while(cur < right){if(nums[cur] == 0){if(cur != ++left)swap(nums[cur],nums[left]);cur++;}else if(nums[cur] == 2)swap(nums[cur],nums[--right]);else//nums[cur] == 1cur++;}}
};题目2: 排序数组

快排最核心的一步就是 Partition (分割数据): 将数据按照一个标准, 分成左右两部分.
但是如果我们用上一题 三路划分 的思想,将数组划分为 左 中 右 三部分:左边是比基准元素小的数据, 中间是与基准元素相同的数据, 右边是比基准元素大的数据, 然后再去递归的排序左边部分和右边部分即可 (可以舍去大量的中间部分).
在处理数据量有很多重复的情况下,效率会大大提升
注意:
1. 用随机数取基准值可以有效缓解一边倒的问题
2. 小区间用插入排序优化速度.
(具体说明见 数据结构之排序 文章)
class Solution {
public:void InsertSort(vector<int>& nums, int left, int right){for(int i = left+1; i <= right; i++){for(int j = i; j > left; j--){if(nums[j] < nums[j-1])swap(nums[j],nums[j-1]);elsebreak;}}}void _sortArray(vector<int>& nums, int begin, int end){if(begin >= end)return;//小区间优化if(end-begin+1 <= 10){InsertSort(nums, begin, end);return;}//随机数取基准元素int key = nums[begin + random()%(end-begin+1)];//三路划分int cur = begin, left = begin-1, right = end+1;while(cur < right){if(nums[cur] < key){if(cur != ++left)swap(nums[left],nums[cur]);cur++;}else if(nums[cur] > key)swap(nums[--right],nums[cur]);elsecur++; }_sortArray(nums,begin,left);_sortArray(nums,right,end);}vector<int> sortArray(vector<int>& nums) {srand(time(NULL));_sortArray(nums,0,nums.size()-1);return nums;}
};
题目3: 数组中的第K大的元素

法一: 排序
时间复杂度O(N*logN), 具体见 C++栈与队列 文章
法二: 优先级队列
时间复杂度O(N*logK), 具体见 C++栈与队列 文章
法三: 快速选择算法
随机选择基准元素 + 三路划分:
注意这个题目的描述, 也就是说假如有n个相同的数字, 它代表n个数而不是1类数
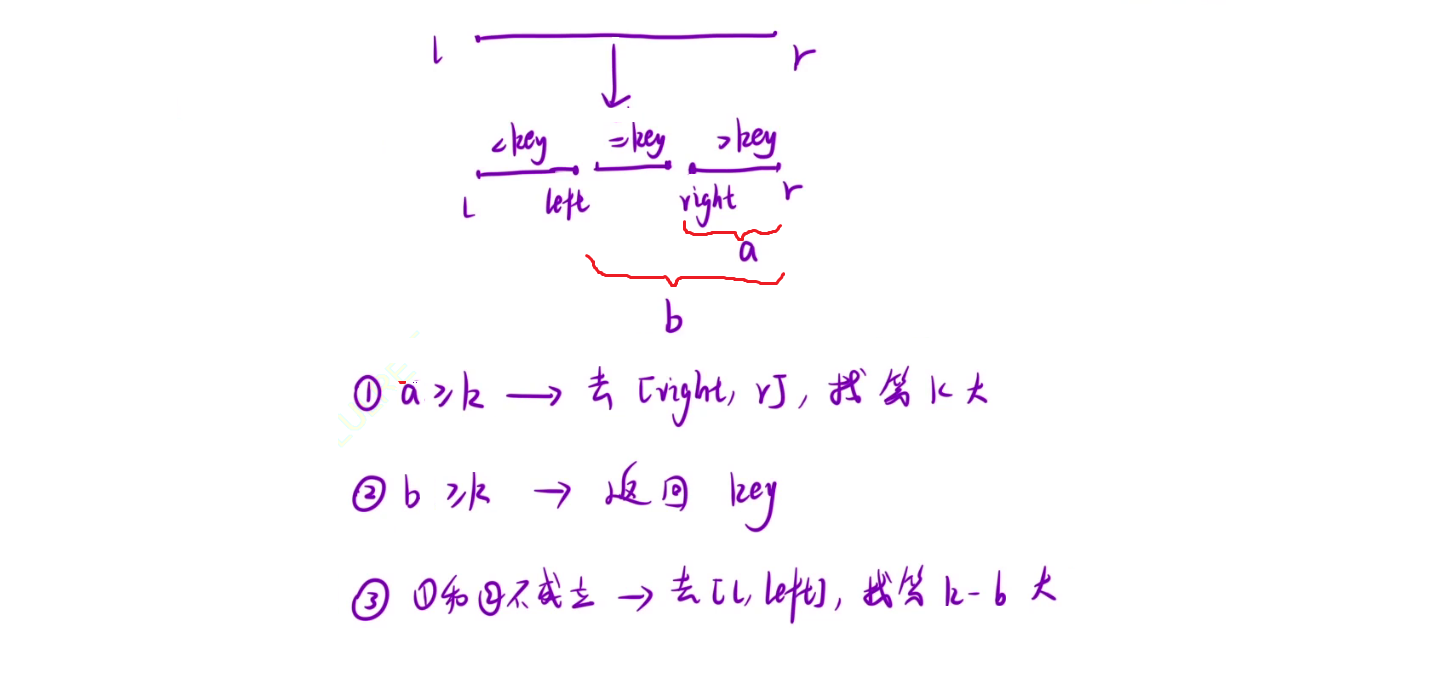
1. a代表比key大的数的个数, 如果a>=k, 说明第k大的数就在这个区间里;
2. b代表大于等于key的数的个数, 如果a <k<=b, 那么key一定是第k大的数;
3. 如果k>b则应该去左区间寻找第k-b大的数.
class Solution {
public:int qsort(vector<int>& nums, int begin, int end, int k){int left = begin-1, right = end+1, cur = begin;int key = nums[begin + rand()%(end-begin+1)];//随机数作为基准值while(cur < right){if(nums[cur] < key){if(cur != ++left)swap(nums[cur],nums[left]);cur++;}else if(nums[cur] > key)swap(nums[cur],nums[--right]);elsecur++;}//[begin,left][left+1,right-1][right,end]int a = end-right+1, b = end-left;if(k <= a)return qsort(nums,right,end,k);else if(k <= b)return key;elsereturn qsort(nums,begin,left, k-b);}int findKthLargest(vector<int>& nums, int k) {return qsort(nums,0,nums.size()-1,k);}
};时间复杂度O(N)
题目4: 最小的 k 个数

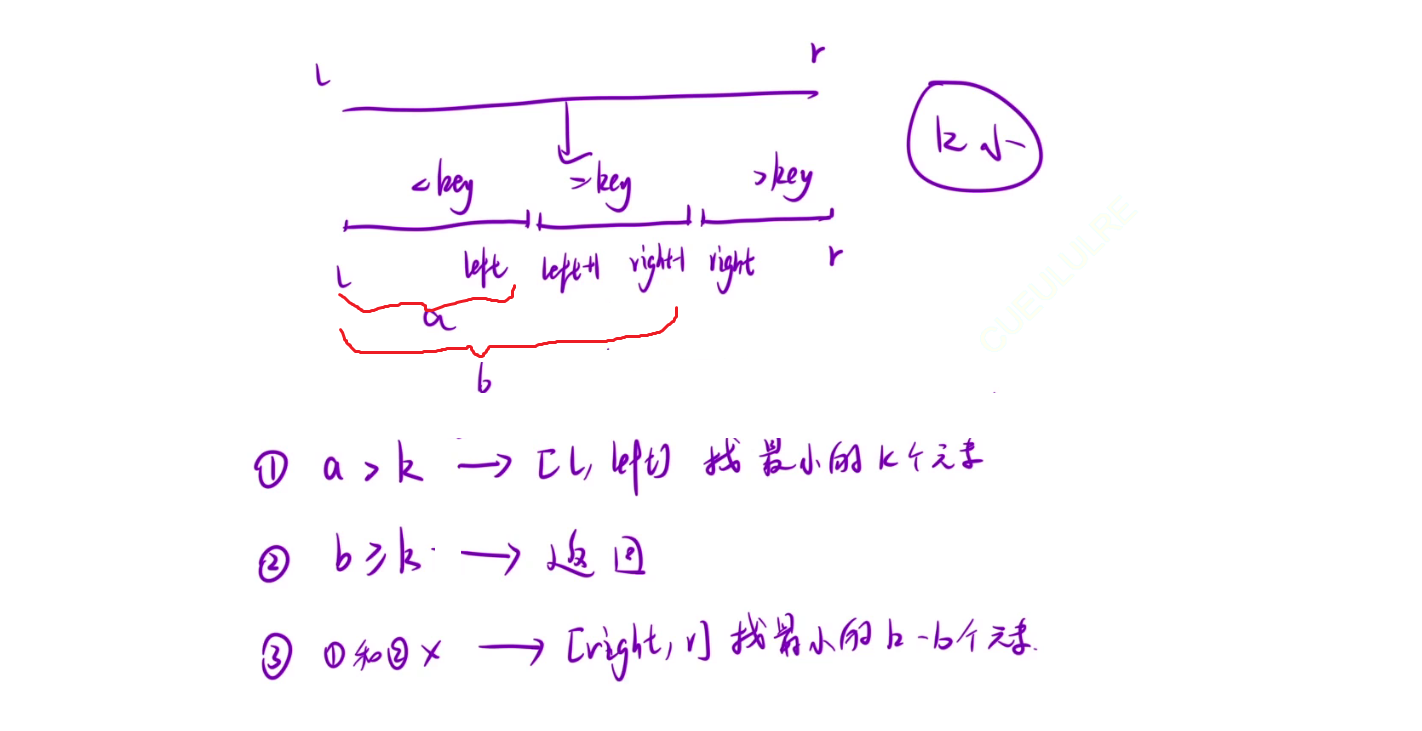
注意: 因为这里找的是前k小, 所以k=a的情况可以合并到b>=k中, 因为k=a那么前a个元素就是前k小, 不需要管大小.
class Solution {
public:void Partition(vector<int>& stock, int begin, int end, int k){ int left = begin-1, right = end+1, cur = begin;int key = stock[begin + rand()%(end-begin+1)];while(cur < right){if(stock[cur] < key){if(cur != ++left)swap(stock[cur],stock[left]);cur++;}else if(stock[cur] > key)swap(stock[cur],stock[--right]);elsecur++;}int a = left -begin;int b = right - begin;if(k <= a)Partition(stock, begin, left, k);else if (k <= b)return;elsePartition(stock, right, end, k - b);}vector<int> inventoryManagement(vector<int>& stock, int cnt) {Partition(stock, 0, stock.size()-1, cnt);return {stock.begin(),stock.begin()+cnt};}
};归并排序
题目1: 排序数组
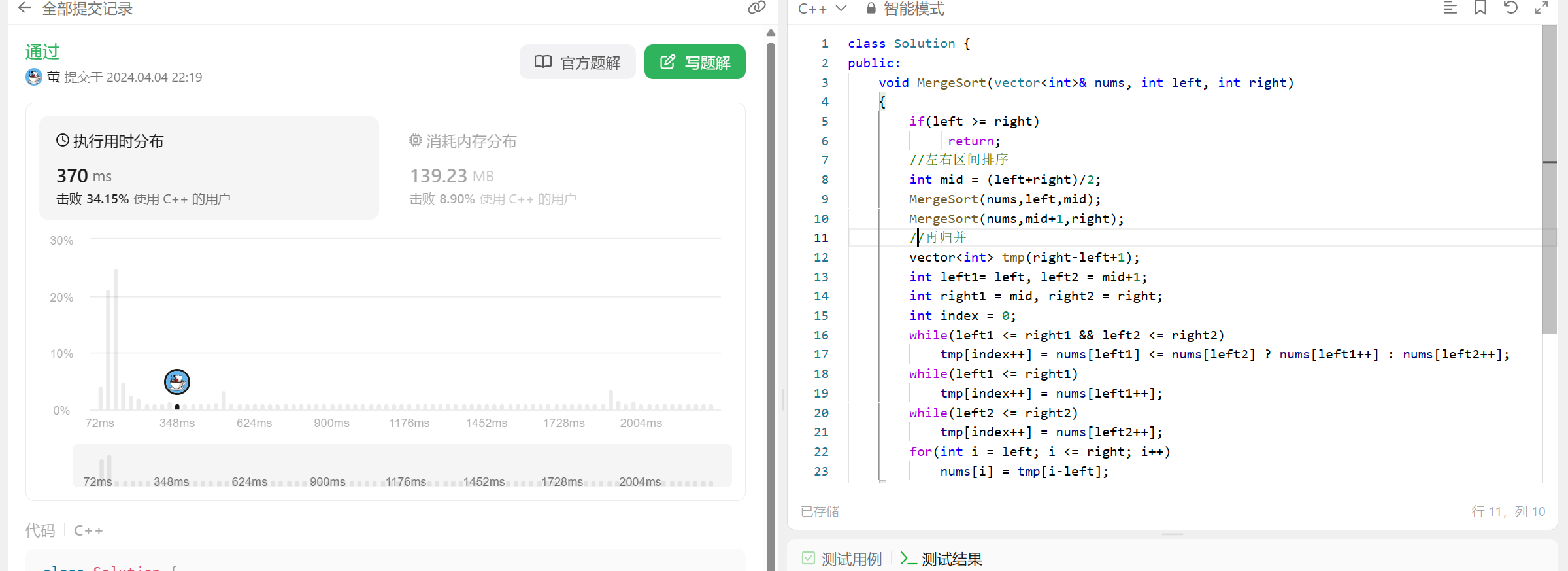
 归并排序的代码不作说明, 主要看tmp 放在局部每次递归创建 和 放在全局一次开辟好 两者的时间消耗差异:
归并排序的代码不作说明, 主要看tmp 放在局部每次递归创建 和 放在全局一次开辟好 两者的时间消耗差异:
tmp在局部创建:
class Solution {
public:void MergeSort(vector<int>& nums, int left, int right){if(left >= right)return;//左右区间排序int mid = (left+right)/2;MergeSort(nums,left,mid);MergeSort(nums,mid+1,right);//再归并vector<int> tmp(right-left+1);int left1= left, left2 = mid+1;int right1 = mid, right2 = right;int index = 0;while(left1 <= right1 && left2 <= right2)tmp[index++] = nums[left1] <= nums[left2] ? nums[left1++] : nums[left2++];while(left1 <= right1)tmp[index++] = nums[left1++];while(left2 <= right2)tmp[index++] = nums[left2++];for(int i = left; i <= right; i++)nums[i] = tmp[i-left];}vector<int> sortArray(vector<int>& nums) {MergeSort(nums,0,nums.size()-1);return nums;}
};
tmp提前开辟好:
class Solution {
public:vector<int> tmp;void MergeSort(vector<int>& nums, int left, int right){if(left >= right)return;//左右区间排序int mid = (left+right)/2;MergeSort(nums,left,mid);MergeSort(nums,mid+1,right);//再归并int left1= left, left2 = mid+1;int right1 = mid, right2 = right;int index = 0;while(left1 <= right1 && left2 <= right2)tmp[index++] = nums[left1] <= nums[left2] ? nums[left1++] : nums[left2++];while(left1 <= right1)tmp[index++] = nums[left1++];while(left2 <= right2)tmp[index++] = nums[left2++];for(int i = left; i <= right; i++)nums[i] = tmp[i-left];}vector<int> sortArray(vector<int>& nums) {tmp.reserve(nums.size());MergeSort(nums,0,nums.size()-1);return nums;}
};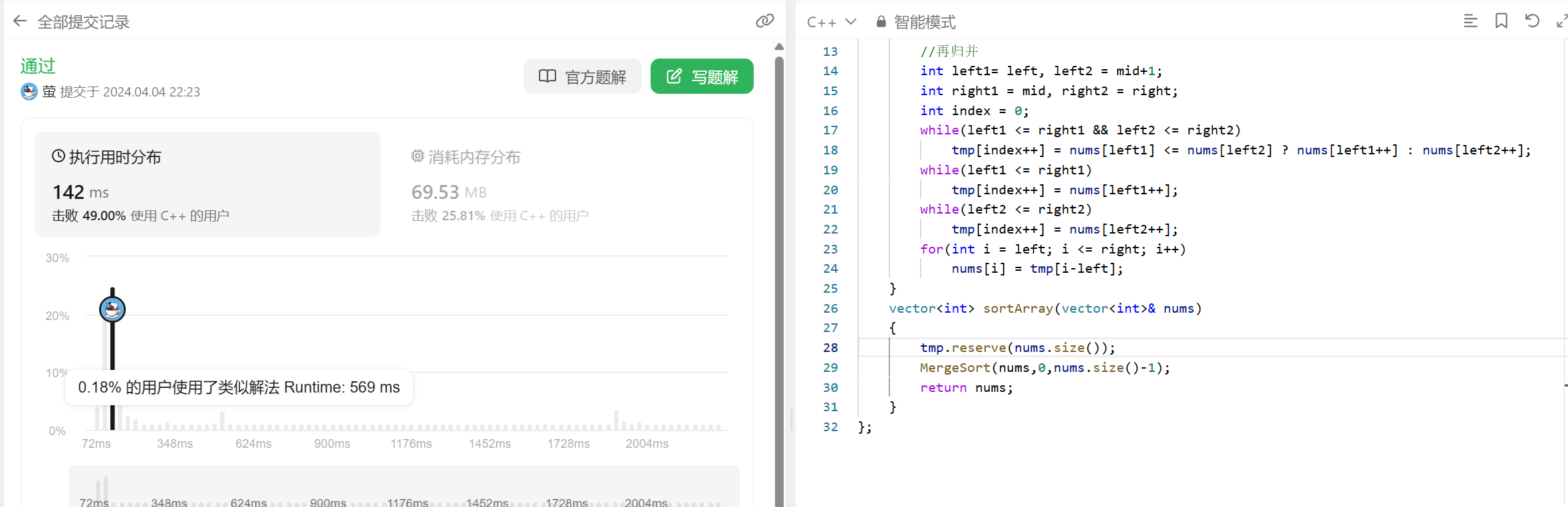
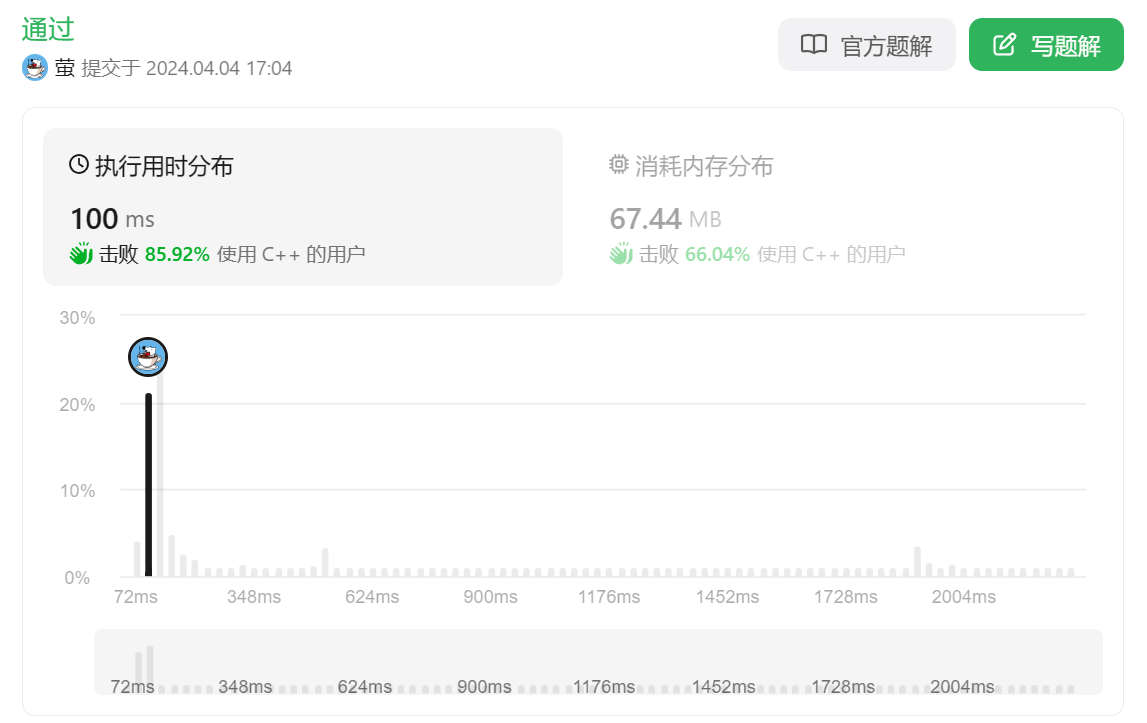
可以看到两者时间消耗近乎两倍, 所以涉及递归开辟空间最好提前把空间开辟好.
题目2: 数组中的逆序对

利用分治法解决该题目, 首先可以考虑到, record里的逆序对的个数等于将record分为两个区间, 左区间逆序对的个数+右区间逆序对的个数+一个数在左区间一个数在右区间凑成的逆序对的个数. 如果单纯只是这样那和暴力枚举都一样, 但给两个区间都排序之后, 会发现问题和归并排序的思路一模一样. 因为给两个区间排序只是区间内局部顺序调整, 两个区间的相对顺序没有改变, 所以可以算出来逆序对.
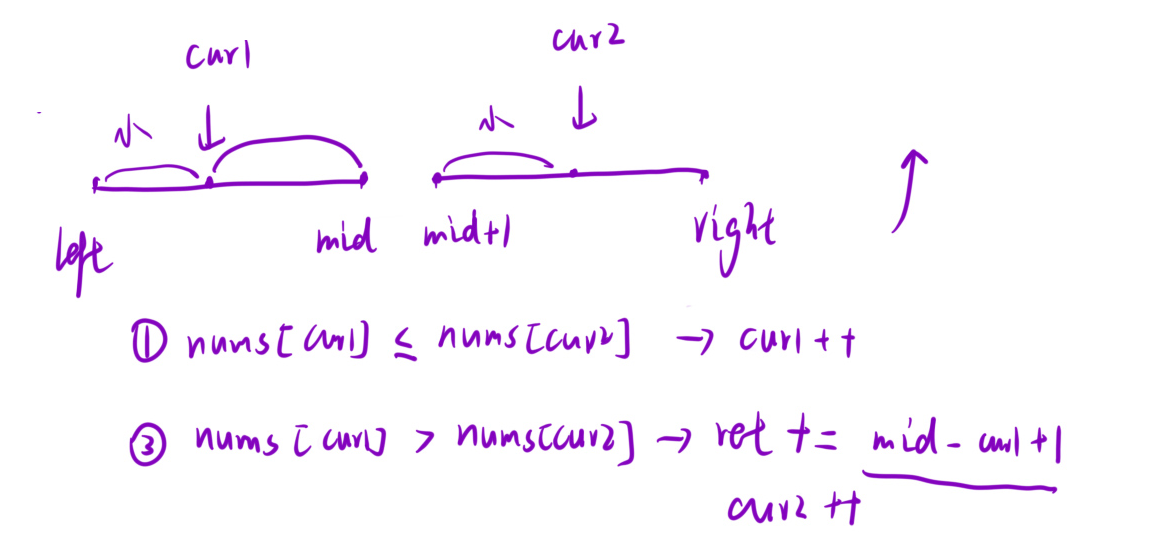
策略1: 找出一个数之前, 有多少个数比我大, 此时要求数组必须是升序:
由于要挑选比我大的数, 所以要在左区间去找大的数, 如果左区间nums[cur1] <= nums[cur2], 那么左边没找到, cur1++; 如果nums[cur1] > nums[cur2], 由于数组是有序的, [cur1, mid]区间内所有的数都是大于nums[cur2]的, 所以记录下这个值, 然后cur2++.
可以发现这个逻辑是和归并排序排升序一模一样的.
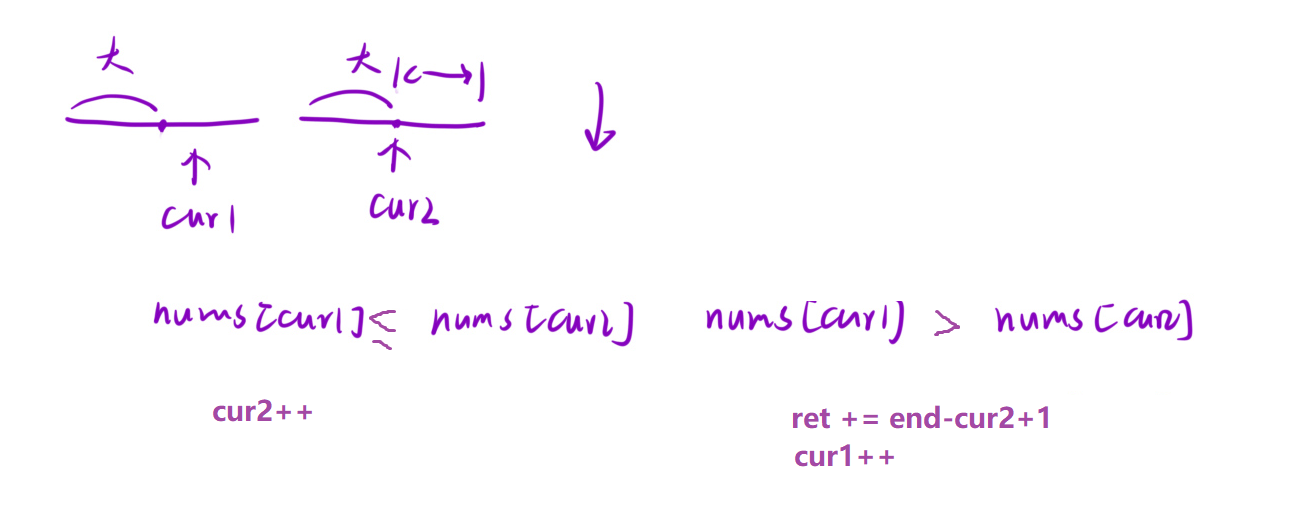
策略2: 找出一个数之后, 有多少个数比我小, 此时要求数组必须是降序:
选比我小的数, 要去右区间找小的数. 如果 nums[cur2] >= nums[cur1], 说明没找到, cur2++;
nums[cur2] < nums[cur1], 找到了, 记录[cur2, end]区间的大小, 然后cur1++;
这个过程是和归并排序排降序一样的.
总结: 找我之前比我大的数, 升序, 看左区间是否小, 小就跳过, 然后归并; 找我之后比我小的数, 看右区间是否大, 大就跳过, 然后归并. (也就是归并排序归并的逻辑)
class Solution {
public:vector<int> tmp;int MergeSort(vector<int>& record, int left, int right){if(left >= right)return 0;int ret = 0;int mid = (right+left)>>1;//ret += MergeSort(record, left, mid);ret += MergeSort(record, mid+1, right);//处理一左一右int left1 = left, left2 = mid+1;int right1 = mid, right2 = right;int index = 0;while(left1 <= right1 && left2 <= right2){if(record[left1] <= record[left2])tmp[index++] = record[left1++];else {ret += (mid-left1+1);tmp[index++] = record[left2++];}}//排序while(left1 <= right1)tmp[index++] = record[left1++];while(left2 <= right2)tmp[index++] = record[left2++];for(int i = left; i <=right; i++)record[i] = tmp[i-left];return ret;}int reversePairs(vector<int>& record) {tmp.reserve(record.size());return MergeSort(record, 0, record.size()-1);}
};题目3: 计算右侧⼩于当前元素的个数

这道题和上一题的逆序对很类似, 但是它需要重新开辟一个counts数组, 还要在counts对应的原始下标处记录以该数为逆序对左元素时的逆序对个数, 关键就在于怎么去确定对应的index:
我们首先会想到用哈希表映射, 但是如果nums有重复元素x, 最后 count[hash[x]] 对应的是所有重复x产生的逆序对个数, 显然不正确, 所以考虑用一个index数组去维护下标, 关键是要在排序的过程中对于下标i, nums[i]和index[i]要同时移动, 保证它们的位置时刻绑定在一起:

由于要多维护一个index数组, 维护比一般的归并排序要麻烦一些, 合并的过程中需要有tmp_num去维护nums, tmp_index去维护index: (代码中用hash命名而不是index)
class Solution {
public:vector<int> tmp_num;vector<int> tmp_index;vector<int> hash;vector<int> counts;void MergeSort(vector<int>& nums, int left, int right){if(left >= right)return;int mid = (left+right)/2, index = 0;MergeSort(nums,left,mid);MergeSort(nums,mid+1,right);int left1 = left, end1 = mid;int left2 = mid+1, end2 = right;while(left1<=end1 && left2<=end2){if(nums[left2] >= nums[left1]){tmp_num[index] = nums[left2];tmp_index[index] = hash[left2];index++;left2++;}else{counts[hash[left1]] += (end2-left2+1);tmp_num[index] = nums[left1];tmp_index[index] = hash[left1];index++;left1++;}}while(left1<=end1){tmp_num[index] = nums[left1];tmp_index[index] = hash[left1];index++;left1++;}while(left2<=end2){tmp_num[index] = nums[left2];tmp_index[index] = hash[left2];index++;left2++;}for(int i = left; i <= right;i++){nums[i] = tmp_num[i-left];hash[i] = tmp_index[i-left];}}vector<int> countSmaller(vector<int>& nums) {int n = nums.size();tmp_num.reserve(n);tmp_index.reserve(n);hash.reserve(n);counts.resize(n,0);for(int i = 0; i < n;i++)hash[i] = i;MergeSort(nums, 0, n-1);return counts;}
};题目4: 翻转对

策略一: 计算当前元素后面, 有多少元素的两倍比我小
对两个降序的区间进行判断, 在右区间找小, 固定cur1, 移动cur2, 若2*nums[cur2] >= nums[cur1], cur2++; 找到了就算出[cur2, end2]长度, 随后cur1++, cur2不需要回退, 因为对于x∈[left2, cur2], 2*x >= nums[cur1], 而对于y∈[cur1,end2], nums[cur1] >= y , 故2*x >= y, 所以 cur2 不需要回退.
在这里cur1和cur2是两个同向双指针
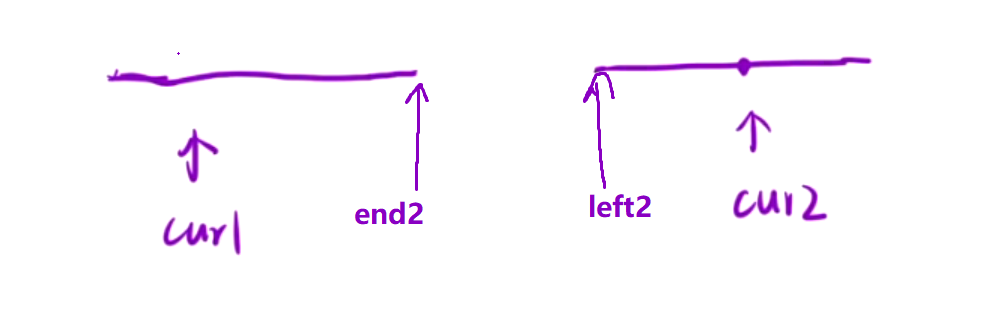
注意, 这里的判断逻辑和归并排序不能合并起来, 之前的逆序对是恰好判断逻辑和归并排序一模一样, 而这里需要单独进行计算.
策略二: 计算当前元素前面, 有多少元素的两倍比我大
同理
class Solution {
vector<long long> tmp;
public:int MergeSort(vector<long long>& record, int left, int right){if(left >= right)return 0;int ret= 0;//1. 先根据中间元素划分区间int mid = (left+right)/2, index = 0;//2. 计算左右两侧的翻转对ret += MergeSort(record, left, mid);ret += MergeSort(record, mid+1, right);int begin1 = left, end1 = mid;int begin2 = mid+1, end2 = right;//3. 双指针, 计算翻转对的数量int cur1 = begin1, cur2 = begin2;while(cur1 <= end1)//降序{while(cur2 <= end2 && record[cur2]*2 >= record[cur1])cur2++;//cur2到末尾直接breakif(cur2 > end2)break;ret += end2-cur2+1;cur1++;}//合并两个有序数组while(begin1 <= end1 && begin2<=end2){if(record[begin2] >= record[begin1])tmp[index++] = record[begin2++];elsetmp[index++] = record[begin1++];}while(begin1 <= end1)tmp[index++] = record[begin1++];while(begin2 <= end2)tmp[index++] = record[begin2++];for(int i = left; i <=right;i++)record[i] = tmp[i-left];return ret;}int reversePairs(vector<int>& nums) {int ret = 0;tmp.reserve(nums.size());vector<long long> nums_L(nums.begin(),nums.end());return MergeSort(nums_L, 0, nums.size()-1);}
};