代码随想录 | Day18 | 二叉树:完全二叉树的节点个数&&平衡二叉树
主要学习内容:
1.完全二叉树的性质,满二叉树的节点数量的计算
2.树的高度和深度问题要用后序遍历更加合适
222.完全二叉树的节点个数
222. 完全二叉树的节点个数 - 力扣(LeetCode)
解法一:直接遍历
前序遍历
class Solution {
public:int res;void r(TreeNode *t){if(t==nullptr)return;res++;r(t->left);r(t->right);}int countNodes(TreeNode* root) {res=0;r(root);return res;}
};
和求深度一样的后序遍历
class Solution {
public:int r(TreeNode *t){if(t==nullptr)return 0;//统计左子树结点个数int left=r(t->left);//统计右子树int right=r(t->right);//左右子树和加上本节点int res=1+left+right;return res;}int countNodes(TreeNode* root) {return r(root);}
};
解法二:利用完全二叉树的性质
如果是一颗满二叉树的话,节点数量=2^树的深度-1
如果是一颗完全二叉树的话,一直递归总可以找到满二叉树

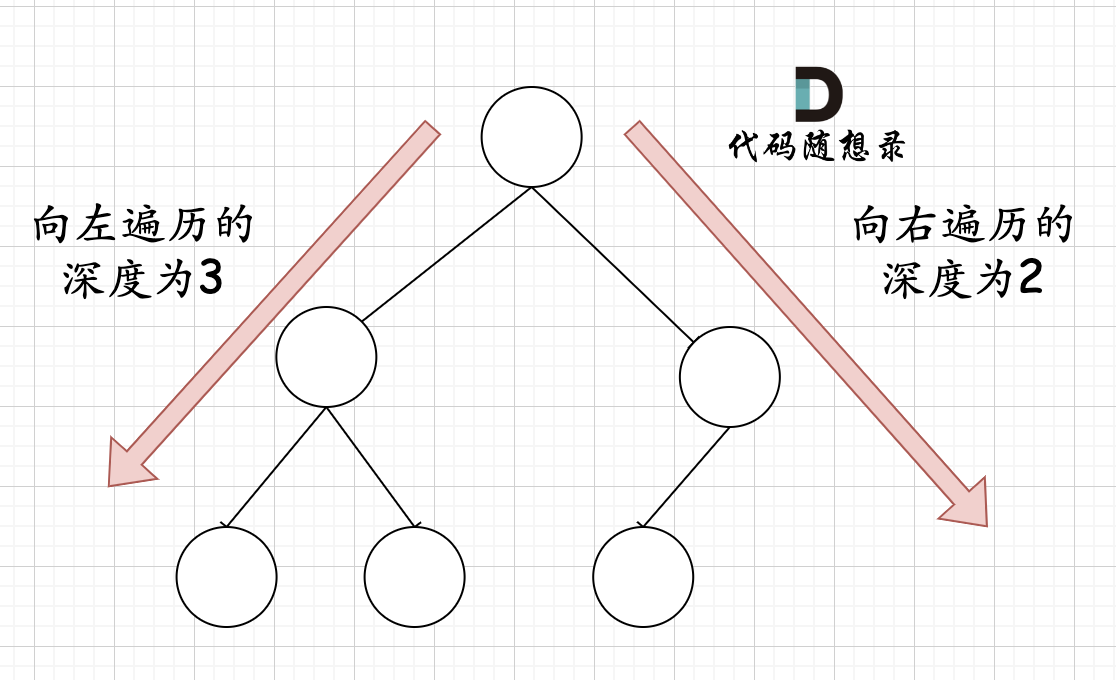
先让左右指针都向下遍历,求出本棵树的左边深度和右边深度,两者如果一样就可以用满二叉树的公式计算本节点的子树的节点数量
因为它是完全二叉树,所以左右指针求出的两个深度相等的话,那它一定是满二叉树
if(t==nullptr)return 0;TreeNode *left=t->left;TreeNode *right=t->right;int l=0,r=0;while(left){l++;left=left->left;}while(right){r++;right=right->right;}if(l==r)return (2<<l)-1;
如果是满二叉树那就用公式求出深度
if(l==r)return (2<<l)-1;
如果不是的话就要继续遍历左子树和右子树,将两者数量相加再加1就是所有的节点数量
int ll=tr(t->left);int rr=tr(t->right);int res=ll+rr+1;return res;

完整代码:
class Solution {
public:int tr(TreeNode *t){if(t==nullptr)return 0;TreeNode *left=t->left;TreeNode *right=t->right;int l=0,r=0;while(left){l++;left=left->left;}while(right){r++;right=right->right;}if(l==r)return (2<<l)-1;int ll=tr(t->left);int rr=tr(t->right);int res=ll+rr+1;return res;}int countNodes(TreeNode* root) {return tr(root);}
};
110.平衡二叉树
110. 平衡二叉树 - 力扣(LeetCode)
由前面的做题经验,我们要得到树的高度来进行高度差的计算,那么肯定会使用的是后序遍历了,因为要使用下层的结果来进行运算
而递归函数的返回值代表的就是本棵树是否是平衡二叉树,-1代表不是,如果是平衡二叉树,则返回的是该子树的最大深度,以便于返回给上层函数后进行比较和运算
1.函数参数和返回值
int r(TreeNode *t)
2.终止条件
为空的结点的高度自然为0
if(t==nullptr)return 0;
3.本层逻辑
如果左边是-1说明左子树不是平衡二叉树
则该子树也不是,右子树同理
如果左右子树都平衡但是两者的最大深度只差大于1,那么本子树也不是平衡二叉树
小于1的话就说明三个条件都符合,本子树为二叉平衡树
int left=r(t->left);if(left==-1)return -1;int right=r(t->right);if(right==-1)return -1;if(abs(left-right)>1)return -1;elsereturn 1+max(left,right);
完整代码:
class Solution {
public:int r(TreeNode *t){if(t==nullptr)return 0;int left=r(t->left);if(left==-1)return -1;int right=r(t->right);if(right==-1)return -1;if(abs(left-right)>1)return -1;elsereturn 1+max(left,right);}bool isBalanced(TreeNode* root) {if(r(root)==-1)return false;return true;}
};