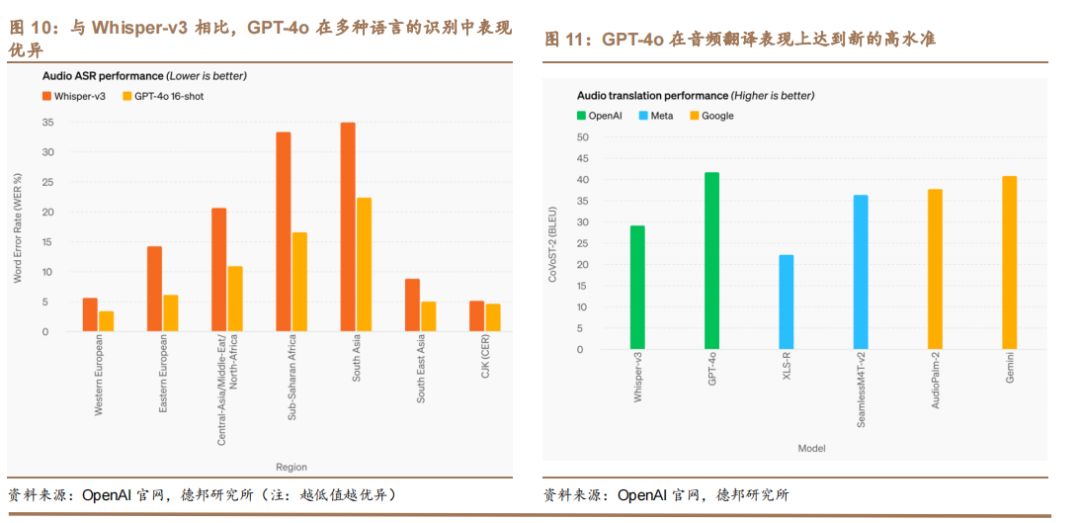
斜率优化详解

斜率优化

[HNOI2008] 玩具装箱

状态转移方程：
$f_i=min(f_i,f_j+(sum_i+i-sum_j-j-L)^2){i>j}$
设A为 $sum_i+i$ ，B为 $sum_j+j+L+1$

简化可得：
$f_i=min(f_i,f_j+A^2-2AB+B^2)$
稍微分解一下，有：
$f_i=f_j+A^2-2AB+B^2 \\ f_j+B^2=2AB+f_i-A^2$
设 $f_j+B^2$ 为点 $y$ ， $2 A$ 为 $k$ ， $B$ 为 $x$ ， $f_i-A^2$ 为 $b$ 。

考虑一个确定的点 $B,f_j+B^2)$ ， $k = 2 A$ 的最小截距。

对于每个确定的 $i$ ，可令斜率为 $h_i$ 的直线过每个决策点，都可求得一个截距。根据状态转移方程可知，其中截距最小的直线方程所经过的决策点即为左右决策。

斜率：

先看一张图：

斜率（↑↑↑）

斜率就是坡度，是高度的平均变化率，用坡度来刻划道路的倾斜程度，也就是用坡面的切直高度和水平长度的比，相当于在水平方向移动一千米，在切直方向上升或下降的数值，这个比值实际上就表示了坡度的大小。

即：设 $(0, 0)$ 点为 $a$ ， $(3, 0)$ 点为 $b$ ，则点 $B$ 的斜率为 $\frac{|b-a|}{B-b}$ 。

以下称 $x_j$ 为 $x$ 轴的 $j$ 点， $y_i$ 为在 $y$ 轴的 $i$ 点。

在绝v额集合中筛选出部分决策，使得在 $x_j$ 递增的顺序下，相邻的决策点所炼成的线段的斜率单调递增。对于任意连续的三个所选决策 $j_{i-1},j_{i},j_{i+1}$ ，都有：
$\frac{f_{j_{i}}-f_{j_{i-1}}}{x_{j_i}-x_{j_{i-1}}}<\frac{f_{j_{i+1}}-f_{j_{i}}}{f_{j_{i+1}}-f_{j_i}}$
在对应坐标系中，相邻点之间连成的线段呈现出“下凸”形态，即为“凸包”。

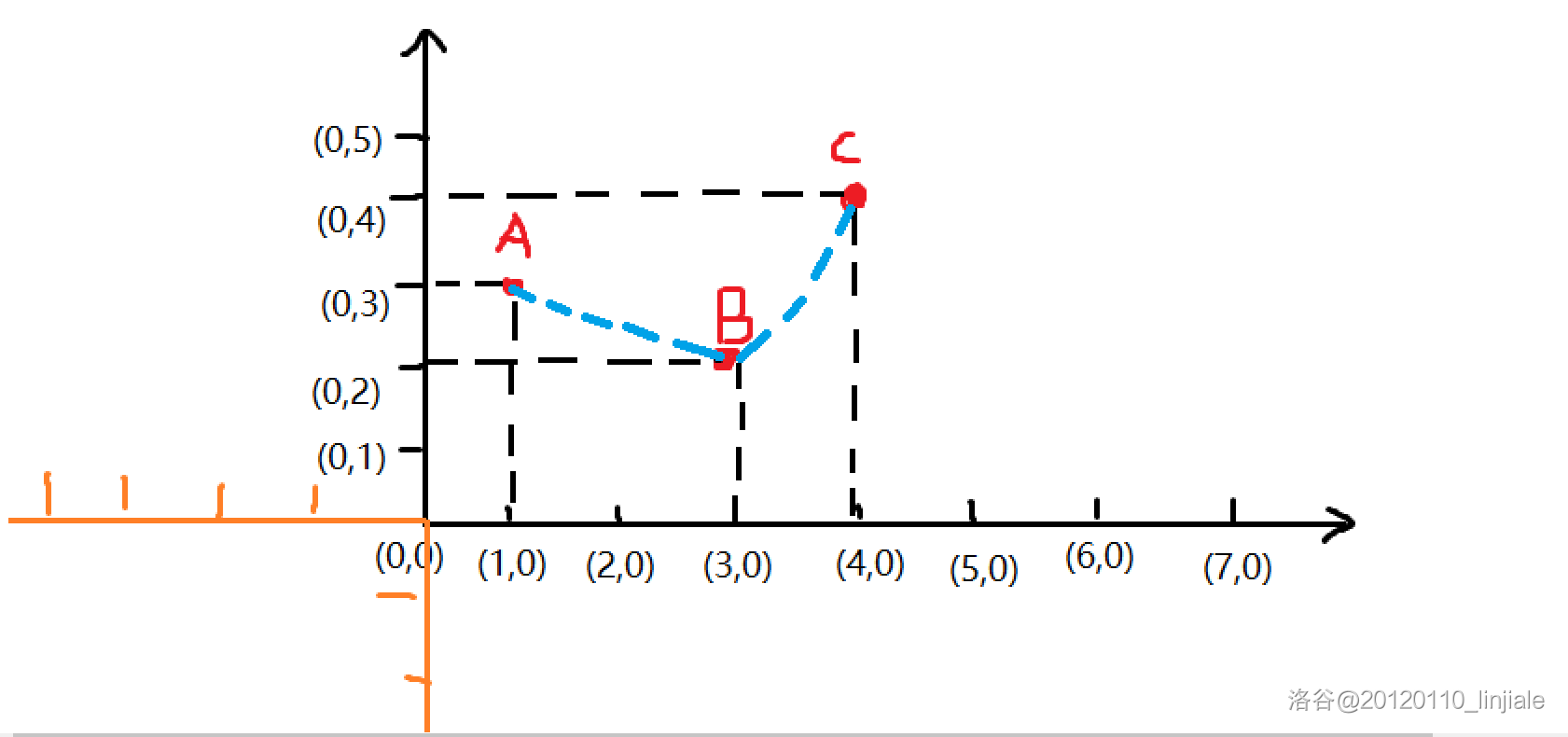
凸包（↑↑↑）

若斜率函数 $h_i$ 与 $x_j$ 均为单调递增函数，随着 $j$ 的递增，决策点的横坐标也单调递增，新决策必定会出现在整个凸包的最右端。又因为斜率函数具有单调性，所以每次需要求解的直线斜率 $h_i$ 也单调递增。决策集合仅保留下凸曲线上相邻现代斜率大于 $h_i$ 的剩余决策点，所以曲线最左端的决策点即为最优决策。

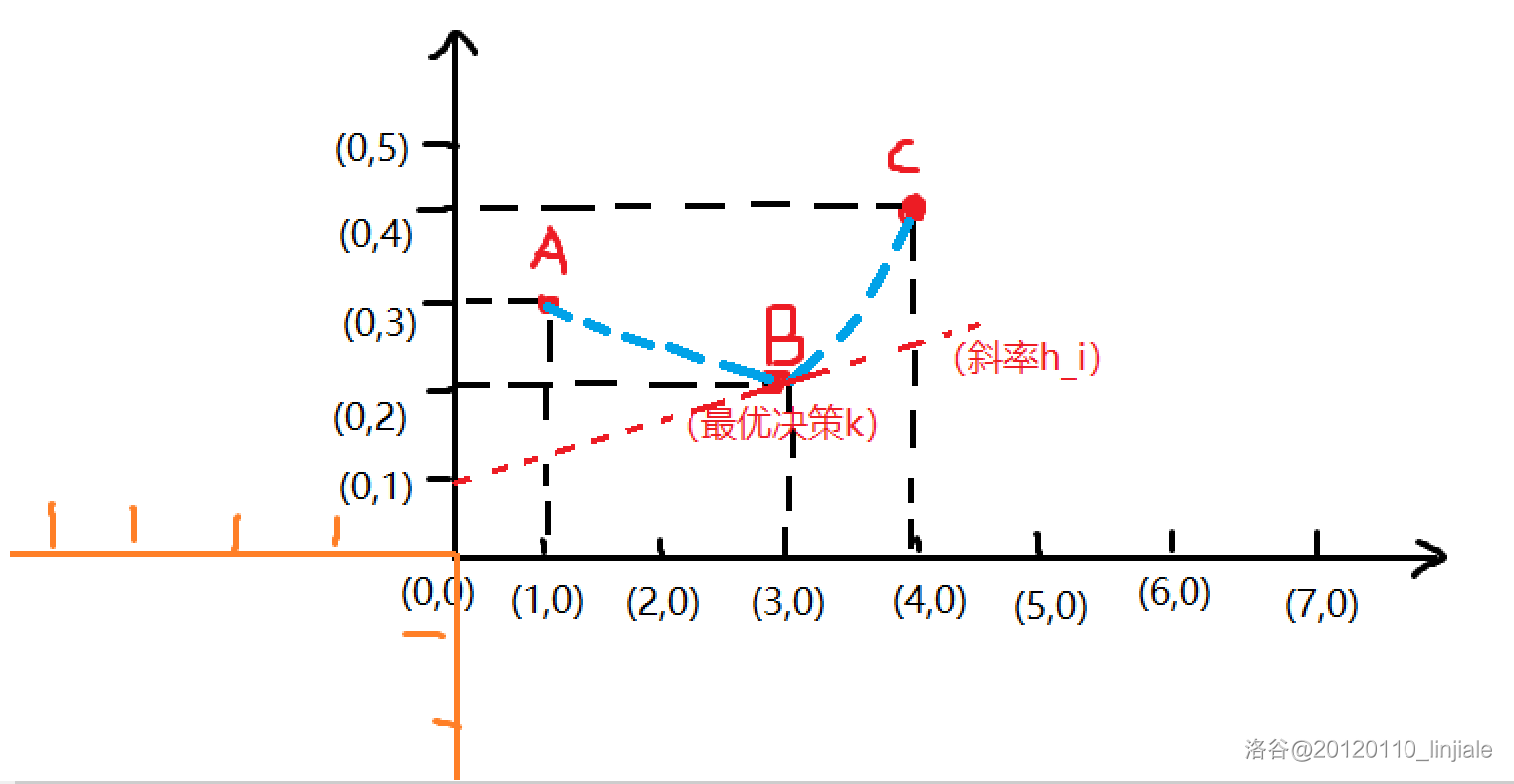
最优决策、最优斜率、截距（设B点为最佳决策点）

根据如上性质，我们不难想出，用双端队列 q[l~r] 维护下凸曲线，队列中保存部分决策，对应下凸曲线上的决策点，满足 $x_i$ 和 $h_i$ 都递增。

具体实施方案：

为了保证队头即为最优决策，仅需保留下凸曲线上斜率大于 $h_i$ 的点，从队头开始检查决策 $q_l$ 和后续决策 $q_{l+1}$ 对应点连接线的斜率。若该斜率小等于 $h_i$ ，则把 $q_l$ 出队，继续检查寻得队头和后续决策，直至线段斜率大于 $h_i$ 。
直接取队头决策 $j=q_l$ 为最优决策，进行状态转移。
将当前状态 $i$ 为新的决策从队尾插入。在插入前需要维护凸曲线性质，即三个决策点 $q_{r-1},q_r,i$ 对应的相邻线段需要满足斜率单调递增，否则吧决策 $q_r$ 出队，继续检查 $q_{r-2},q_{r-1},i$ ，直至满足要求。设此操作一共进行了 $n$ 轮，则最终需要判断的三个状态为 $q_{r-n},q_{r-n+1},i$ 。

时间复杂度： $O (N)$ 。

若斜率函数 $h_i$ 不满足单调性，则 $x_j$ 为单调递增函数，队头不为最优决策，须保留整个下凸曲线，可在队列中二分查找，求出一个位置 $k$ ，使得：

$\forall\ p\ <\ k \\ \forall\ q\ >\ k \\ h_p<h_k<h_q$

若满足以上条件，则 $k$ 为最优决策。

时间复杂度： $\log n)$ 。

AC Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,l;
const ll MAXN=5e4+5;
ll q[MAXN],sum[MAXN],f[MAXN];
ll head=1,tail=1;
ll j;
inline ll x(ll j)//x坐标 
{return sum[j];
}
inline ll y(ll j)//y坐标 
{return f[j]+(sum[j]+l)*(sum[j]+l);
}
inline double slope(ll i,ll j)//计算 
{return (double)(y(j)-y(i))/(x(j)-x(i));
}
inline ll compute(ll i,ll j)//代价公式 
{return (sum[i]-sum[j]-l)*(sum[i]-sum[j]-l);
}
int main(){scanf("%lld%lld",&n,&l);l++;//因为一直都是-l-1，干脆直接变为 -(l+1) for(ll i=1;i<=n;i++){scanf("%lld",&sum[i]);sum[i]+=sum[i-1]+1;//前缀和 }q[tail]=0;for(ll i=1;i<=n;i++)//dp{while(head<tail&&slope(q[head],q[head+1])<=(sum[i]<<1))//出队首条件 head++;j=q[head];//队首 f[i]=f[j]+compute(i,j);//计算 while(head<tail&&slope(q[tail-1],q[tail])>=slope(q[tail-1],i))//出队末条件 tail--;q[++tail]=i;//最优决策入队 }printf("%lld\n",f[n]);return 0;
}