Every day a Leetcode

题目来源：498. 对角线遍历

解法1：模拟

根据题目要求，矩阵按照对角线进行遍历。设矩阵的行数为 m，矩阵的列数为 n，我们仔细观察对角线遍历的规律可以得到如下信息：

1. 一共有 m+n−1 条对角线，相邻的对角线的遍历方向不同。
2. 设对角线从上到下的编号为 i（0<=i<m+n-1），当 i 为偶数时，则第 i 条对角线的走向是从下往上遍历；当 i 为奇数时，则第 i 条对角线的走向是从上往下遍历。

根据以上观察得出的结论，我们直接模拟遍历所有的对角线即可。

代码：

/** @lc app=leetcode.cn id=498 lang=cpp** [498] 对角线遍历*/// @lc code=start
class Solution
{
public:vector<int> findDiagonalOrder(vector<vector<int>> &mat){int m = mat.size(), n = m ? mat[0].size() : 0;// 一共有 m + n - 1 条对角线int lines = m + n - 1;vector<int> ans;for (int i = 0; i < lines; i++){if (i % 2 == 0){ // ↗int x = i < m ? i : m - 1;int y = i < m ? 0 : i - m + 1;while (x >= 0 && y < n){ans.push_back(mat[x][y]);x--, y++;}}else{ // ↙int x = i < n ? 0 : i - n + 1;int y = i < n ? i : n - 1;while (x < m && y >= 0){ans.push_back(mat[x][y]);x++, y--;}}}return ans;}
};
// @lc code=end

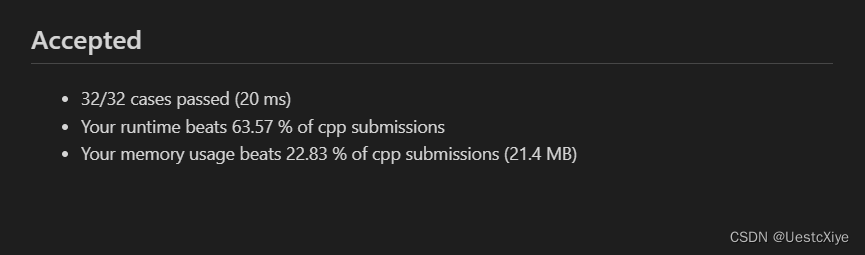
结果：

复杂度分析：

时间复杂度：O(m*n)，其中 m 是矩阵 mat 的行数 ，n 是矩阵 mat 的列数。

空间复杂度：O(1)。