1. Ch10–python 数据图形绘制与可视化

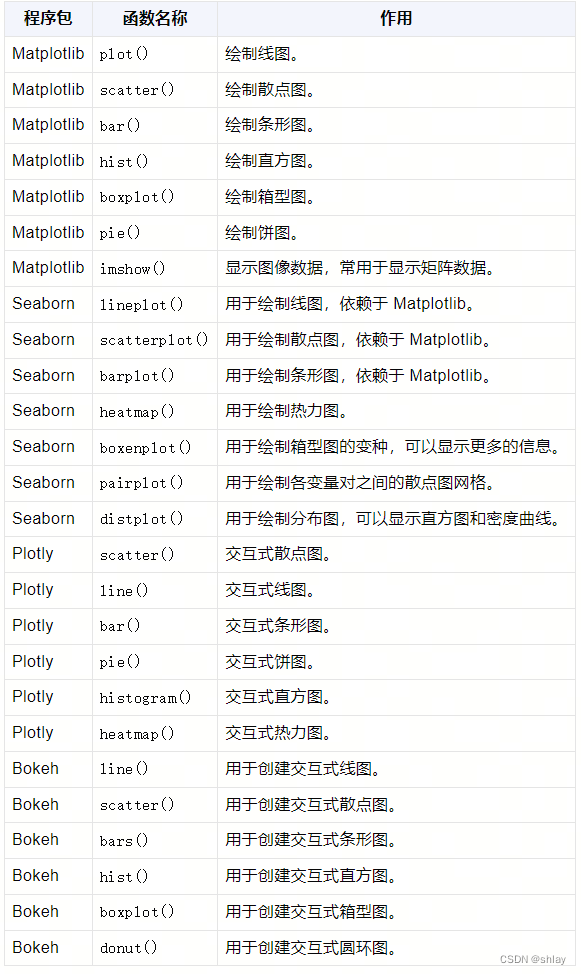
Python 中有多个用于数据可视化的库，其中最常用的包括 Matplotlib、Seaborn、Plotly 和 Bokeh 等。以下是这些库中一些常用图形可视化方法的整理表格：

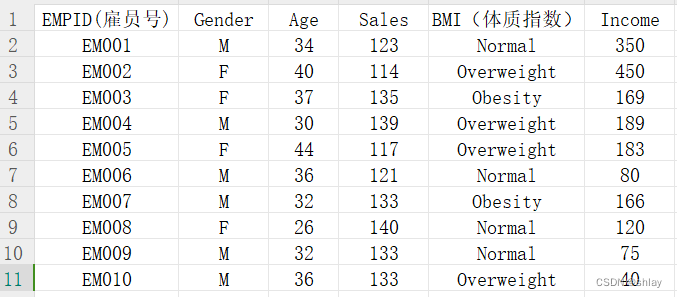
例10-1：为了解某公司雇员的的销售和收入情况，我们搜集整理了某公司10个雇员的销售和收入有关方面的数据，如表10-1所示。试通过绘制直方图来直观该公司职员的有关情况。j

1.1 模块导入

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

1.2 数据导入

python常见数据的存取
dataframe基本操作
数据文件ch10-1.xls下载

df = pd.read_excel('./data/ch10-1.xls')
print(type(df))
df.head()

<class 'pandas.core.frame.DataFrame'>

	EMPID(雇员号)	Gender	Age	Sales	BMI（体质指数）	Income
0	EM001	M	34	123	Normal	350
1	EM002	F	40	114	Overweight	450
2	EM003	F	37	135	Obesity	169
3	EM004	M	30	139	Overweight	189
4	EM005	F	44	117	Overweight	183

2. 绘制直方图

• 特点：直方图用于展示数据的分布情况，通过数据分组（通常是连续的数值区间），显示每个组内的频数或频率。
• 使用场景：当需要了解数据集中数值变量的分布情况时使用。

# %matplotlib inline
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(df['Age'],bins=7)
plt.show()

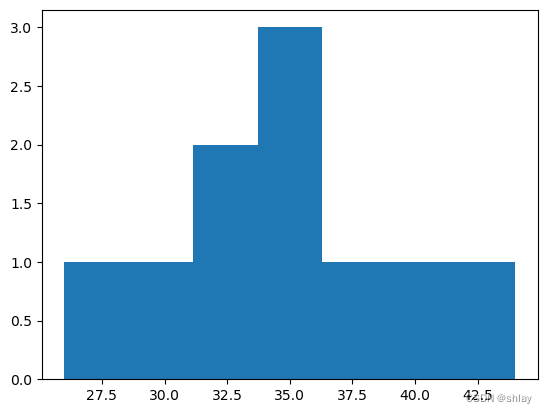
2.1 添加图表题

#中文字符设定 plt.rcParams属性总结
plt.rcParams['font.sans-serif']=['SimHei'] # 1
plt.rcParams['axes.unicode_minus']=False # 2fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(df['Age'],bins=7)
plt.title("年龄分布图") # 3
# plt.title("age distribution")#2-1
plt.show()

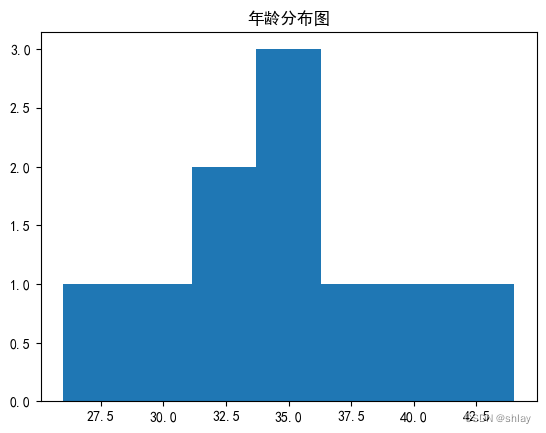
2.2 添加坐标轴标签

#中文字符设定 plt.rcParams属性总结
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(df['Age'],bins=7)
plt.title("年龄分布图") 
plt.xlabel('年龄')
plt.ylabel('雇员数量')
plt.show()

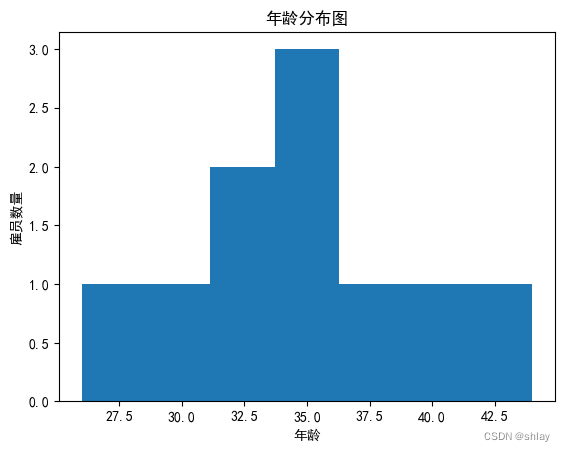
3. 绘制散点图

• 特点：散点图用于展示两个变量之间的关系，每个点代表一个数据项。
• 使用场景：当需要分析两个数值变量之间是否存在某种关系时使用。

fig = plt.figure(figsize=(5, 3))
ax = fig.add_subplot(1,1,1)
ax.scatter(df['Age'],df['Sales'])
plt.title('雇员年龄与销售额的散点图')
plt.xlabel('年龄')
plt.ylabel('销售额')
plt.show()

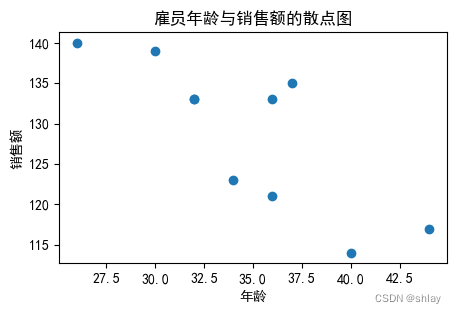
4. 绘制气泡图

• 特点：气泡图是散点图的扩展，通过气泡的大小来表示第三个数值变量的大小。
• 使用场景：当需要在两个数值变量的关系中展示第三个数值变量的大小时使用。

fig = plt.figure(figsize=(5, 3))
ax = fig.add_subplot(1,1,1)
ax.scatter(df['Age'],df['Sales'],s=df['Income'])#引入了第三个变量Income
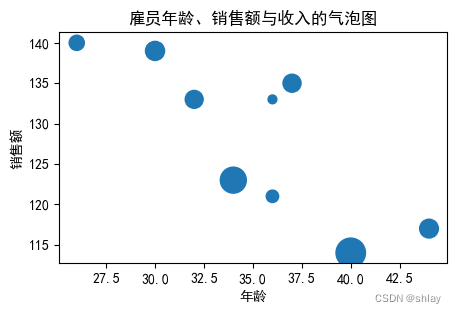
plt.title('雇员年龄、销售额与收入的气泡图')
plt.xlabel('年龄')
plt.ylabel('销售额')
plt.show()

5. 绘制箱线图

• 特点：箱线图用于展示数据的分布情况，包括中位数、四分位数以及异常值。
• 使用场景：当需要了解数据集中数值变量的分布并识别潜在的异常值时使用。

5.1 单特征的箱线图

fig = plt.figure(figsize=(5, 3))
ax = fig.add_subplot(1,1,1)
ax.boxplot(df['Age'])
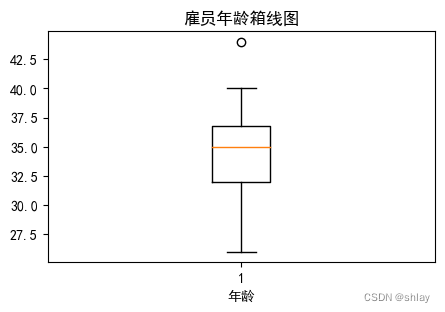
plt.title('雇员年龄箱线图')
plt.xlabel('年龄')
plt.show()

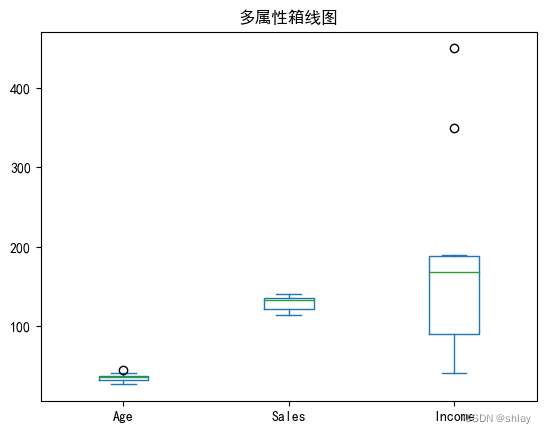
5.2 多特征的箱线图

features = ['Age','Sales','Income']
data = df[features]
print(data.head())
plt.show(data.plot(kind='box',title='多属性箱线图'))

   Age  Sales  Income
0   34    123     350
1   40    114     450
2   37    135     169
3   30    139     189
4   44    117     183

6. 绘制饼图

• 特点：饼图用于展示各部分占整体的比例。
• 使用场景：当需要展示各分类变量占总体的比例时使用。

比较男雇员与女雇员的销售收入

# Step1 分组计算男女雇员的收入之和
sum_income = df.groupby(['Gender']).sum().stack()
print(sum_income)

Gender            
F       EMPID(雇员号)                             EM002EM003EM005EM008Age                                                     147Sales                                                   506BMI（体质指数）                 OverweightObesityOverweightNormalIncome                                                  922
M       EMPID(雇员号)                   EM001EM004EM006EM007EM009EM010Age                                                     200Sales                                                   782BMI（体质指数）     NormalOverweightNormalObesityNormalOverweightIncome                                                  900
dtype: object

temp = sum_income.unstack()
x_list = temp['Sales']
label_list = temp.index
plt.axis('equal')
# plt.pie(x_list)
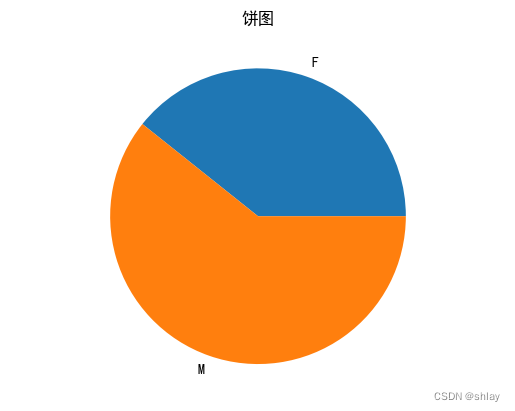
plt.pie(x_list,labels=label_list)
plt.title('饼图')
plt.show()

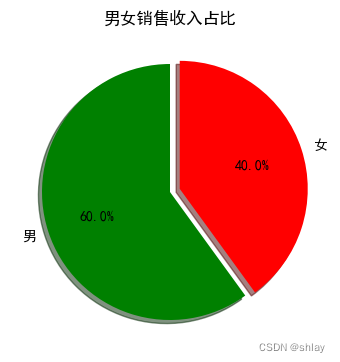
from pylab import *
figure(1, figsize=(4,4))
ax = axes([0.1, 0.1, 0.8, 0.8])
fracs = [60, 40]             #每一块占得比例，总和为100
explode=(0, 0.08)             #离开整体的距离，看效果
labels = '男', '女'  #对应每一块的标志
pie(fracs,explode=explode,labels=labels,autopct='%1.1f%%', shadow=True, startangle=90, colors = ("g", "r"))
title('男女销售收入占比')   #标题
show()

7. 绘制条形图

• 特点：条形图用于比较不同类别的数值大小。
• 使用场景：当需要比较不同分类变量的数值时使用。

7.1 简单条形图

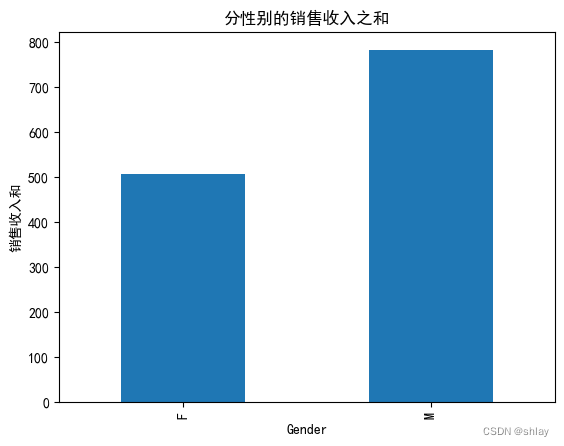
var=df.groupby('Gender').Sales.sum()
fig=plt.figure()
ax1=fig.add_subplot(1,1,1)
ax1.set_xlabel('性别')
ax1.set_ylabel('销售收入和')
ax1.set_title("分性别的销售收入之和")
var.plot(kind='bar')

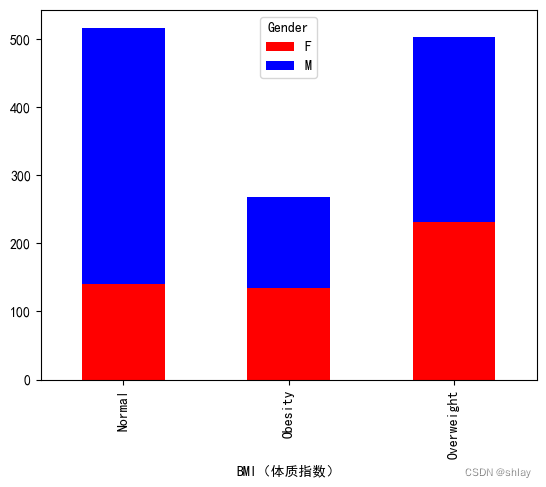
7.2 堆积柱形图

var=df.groupby(['BMI（体质指数）','Gender']).Sales.sum()
var.unstack().plot(kind='bar',stacked=True,color=['red','blue'])

8. 绘制折线图

• 特点：折线图用于展示数据随时间或有序类别的趋势。
• 使用场景：当需要展示数值随时间变化的趋势时使用。

8.1 单折线图

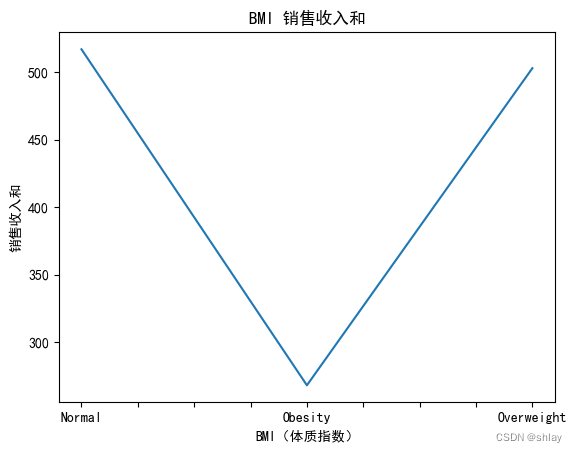
var=df.groupby('BMI（体质指数）').Sales.sum()
fig=plt.figure()
ax1=fig.add_subplot(1,1,1)
ax1.set_xlabel('BMI（体质指数）')
ax1.set_ylabel('销售收入和')
ax1.set_title("BMI分类的销售收入和")
var.plot(kind='line')

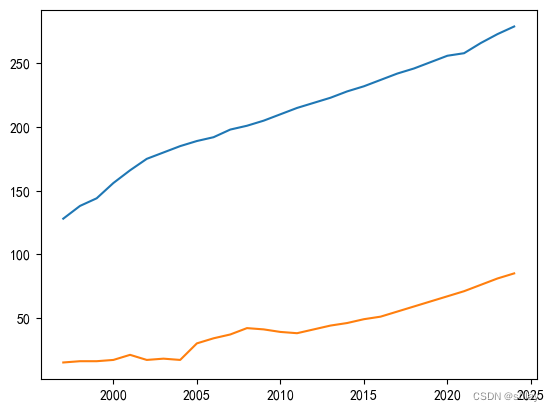
8.2 多折线图

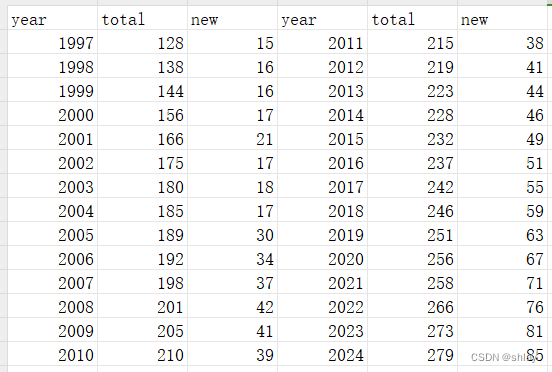
某村每年进行人口普查，该村近年的人口数据如表 ch10-2 所示。

试通过绘制曲线标绘图来分析研究该村的人口情况变化趋势以及新生儿对总人口数的影响程度。

数据文件ch10-2.csv下载

import pandas as pd
import numpy as np
df2=pd.read_csv('./data/ch10-2.csv ')
df2.head()

	year	total	new
0	1997	128	15
1	1998	138	16
2	1999	144	16
3	2000	156	17
4	2001	166	21

t = np.array(df2[['year']])
x = np.array(df2[['total']])
y = np.array(df2[['new']])
import pylab as pl
pl.plot(t, x)
pl.plot(t, y)
pl.show()

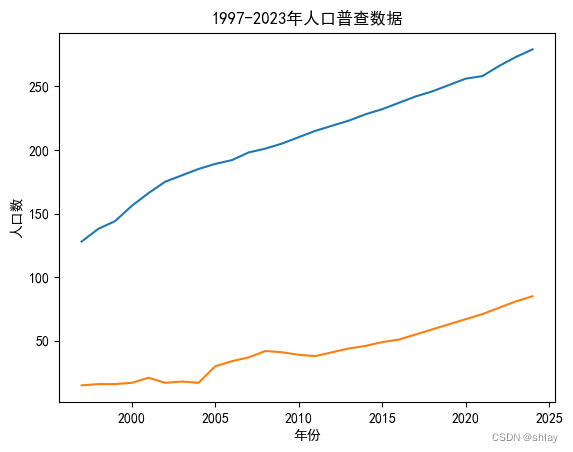
import pylab as pl
pl.plot(t, x)
pl.plot(t, y)
pl.title('1997-2023年人口普查数据')
pl.xlabel('年份')
pl.ylabel('人口数')
pl.show()

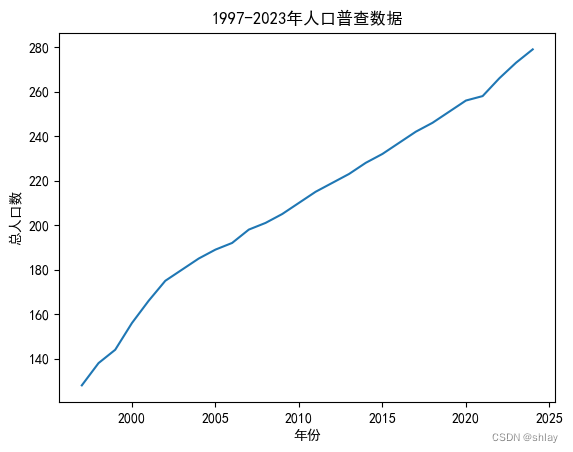
pl.plot(t, x)
pl.title('1997-2023年人口普查数据')
pl.xlabel('年份')
pl.ylabel('总人口数')
pl.show()

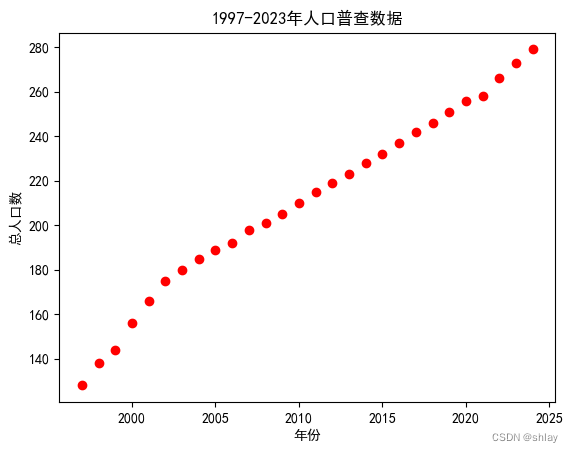
pl.plot(t, x,'ro')
pl.title('1997-2023年人口普查数据')
pl.xlabel('年份')
pl.ylabel('总人口数')
pl.show()

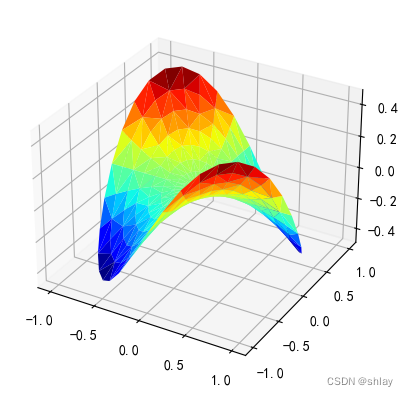
9. 绘制3D图

• 特点：3D图可以展示三个数值变量之间的关系。
• 使用场景：当需要在三维空间中展示数据点的分布时使用。

import random
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from mpl_toolkits.mplot3d import Axes3D

mpl.rcParams['font.size'] = 10
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
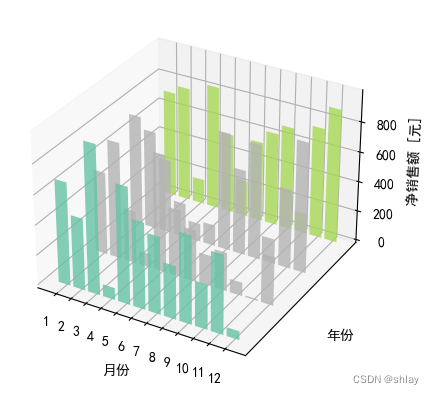
for z in [2011, 2012, 2013, 2014]:xs = range(1,13)ys = 1000 * np.random.rand(12)color =plt.cm.Set2(random.choice(range(plt.cm.Set2.N)))ax.bar(xs, ys, zs=z, zdir='y', color=color, alpha=0.8)
ax.xaxis.set_major_locator(mpl.ticker.FixedLocator(xs))
ax.yaxis.set_major_locator(mpl.ticker.FixedLocator(ys))
ax.set_xlabel('月份')
ax.set_ylabel('年份')
ax.set_zlabel('净销售额 [元]')
plt.show()

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
n_angles = 36
n_radii = 8
# An array of radii
# Does not include radius r=0, this is to eliminate duplicate points
radii = np.linspace(0.125, 1.0, n_radii)
# An array of angles
angles = np.linspace(0, 2 * np.pi, n_angles, endpoint=False)
# Repeat all angles for each radius
angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)
# Convert polar (radii, angles) coords to cartesian (x, y) coords
# (0,0)is added here.There are no duplicate points in the (x, y)plane
x = np.append(0, (radii * np.cos(angles)).flatten())
y = np.append(0, (radii * np.sin(angles)).flatten())
# Pringle surface
z = np.sin(-x * y)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_trisurf(x, y, z, cmap=cm.jet, linewidth=0.2)
plt.show()