一、说明

在许多机器学习的章节中，常常遇见 HMM ，往往看到它的数学式子后，就当没看到似的跳过去了，其实它的基础理论并不难，尤其是 Markov Chain 在高中数学课本就已经出现过了，但…那么久远的事，相信大家都忘得差不多了，现在一起来回顾一下吧!!
在前面 part 2 有提醒大家慎入唷！ 有满满多出来的数学式，要 hold 住呀！底下我们分成几个部分来说明和算法。

二、HMM 三大问题

a. Evaluation Problem — Forward-backward Algorithm
b. Decoding Problem — Viterbi Algorithm
c. Learning Problem — EM Algorithm
d. （补充） Continuous Hidden Markov Chain

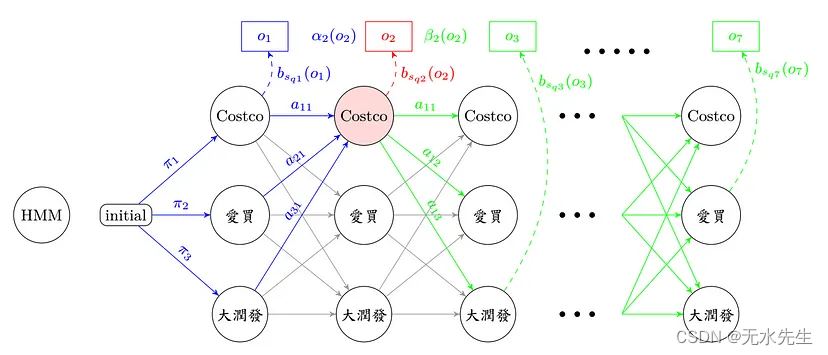
在进入主题前，再重申一次问题，如下图…

我们需计算在已知观察序列 O（o₁， o₂， o₃， …， ot） ，但未知转移矩阵的条件下，找出其对应的的所有可能状态序列 Q（q₁， q₂， q₃， …， qt） ，以及其中最大机率之状态序列。

HMM 三大问题
有些人大概觉得简单吧！ 暴力法就可以解决了，穷举出所有可能的路径，并计算每条路径的机率，不就结束了吗？ 就是每条路径都算过，疴… 时间复杂度是O（N^TT）呀！ 大大，在文明的21世纪，我们不能这么暴力呀！

以下的算法要跟大家介绍，如何降低计算的时间复杂度

三、评估问题——前向-后向算法

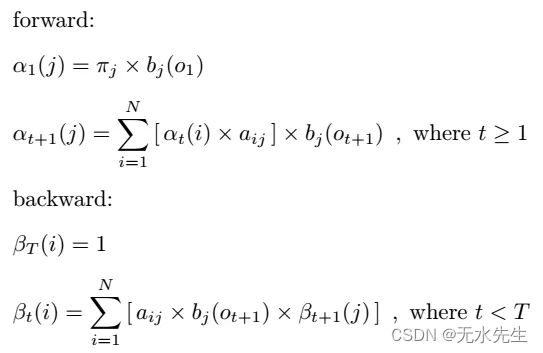
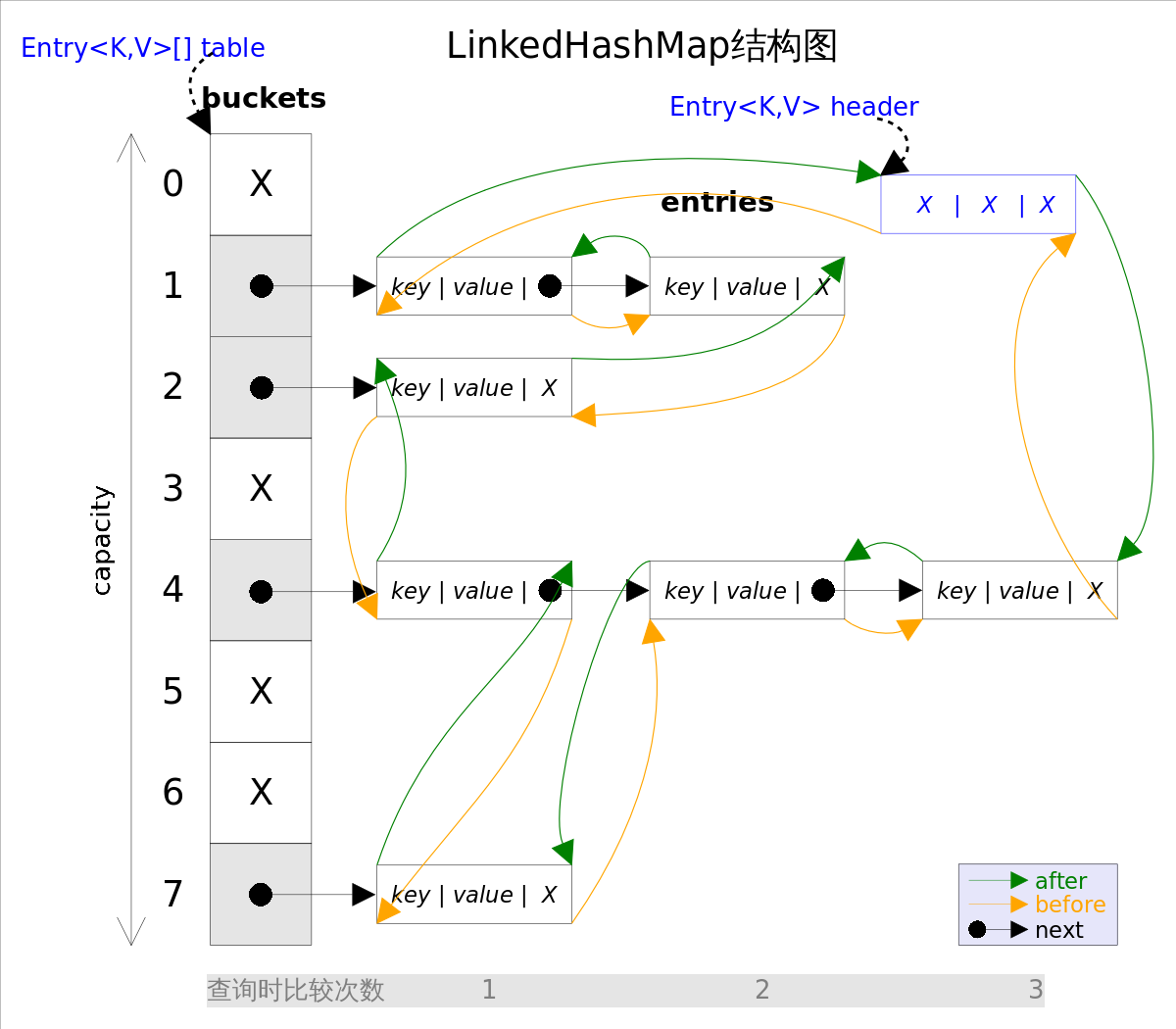
一看到数学式，大概眼花了，所以在这边要搭配图来看，才不会错乱。

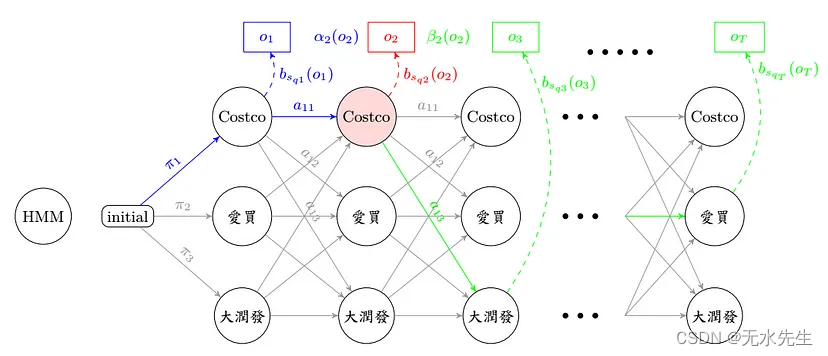
forward 顾名思义，就是由前往后找路径，直到第 t 秒，其实也不太难，看到上图蓝色经过的流程图在这边 forward 要计算的部分只有 αt（j），意思就是在第 t 秒、第 j 个状态，发生 ot 的所有可能路径机率之加总值，所以只算第 t 秒和第 t 秒以前发生的可能路径机率！

backward 用膝盖想，就是由后往前算嘛，看看流程图之绿色部分，βt（j）从第 t 秒开始，考虑由第 j 个状态出发，直至第 T 秒结束的所有路径机率之总和，由于不知道在 t 由 j 状态出发的机率值， 所以我们是从已知第 T 秒发生的机率值，往前回推至第 t 秒的路径机率。

用图标法来看，不严谨的说法是 forward 乘上 backward ，就恰巧是在观察序列 O 时，发生第 t 秒，经过第 j 个状态的所有可能路径机率之总和。

疑？ forward 往后算到底，不就是 backward 往前算到底的值嘛？ 恩，是的，所以要估算路径机率，其实只要算一种就可以了。

何以利吾身？ 这样算有什么好处呢？ 时间复杂度大大的减少了呀！ 只剩下 O（N²T） 唷！ 时间就是金钱，颗颗…不过这个算法既然有 forward 和 backward，算这两个一定有原因呀！ 等等在底下会提到。

四、.解码问题——维特比算法

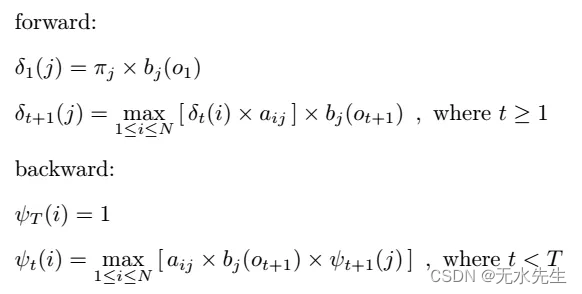
看到这边，应该都是会心一笑，其实和上个算法差不多嘛！ 只是把 ∑ 变成 max 而已呀！ 是的，你没有看错就是这么简单，有别于上个算法是要找出在第 t 秒，会经过第 j 个状态的所有可能路径机率总和，而这个算法想表示的是，在第 t 秒，会经过第 j 个状态之最大机率路径。

五、学习问题——EM算法

Learning Problem 翻译一下，就是学习问题，学习要学什么呢？ 用 part 2 的举例说明一下吧！

过去一年来，我们以周为一个观察序列单位，纪录圆仔每天买饮料的习惯，因此我们想从圆仔的饮料习惯纪录中，分析出「选择买什么东西」、「去哪间卖场购买的」，可惜的是，我们没有纪录到圆仔去哪间卖场买东西的诱因，亦即是「机率」，再换句话说，我们要寻找的训练的目标是找到「状态转移矩阵 A」、「观察转移矩阵 B」、「起始值转移矩阵 π」，而「圆仔的饮料习惯纪录」是我们的训练数据集。

了解问题之后，先来看一下离散问题的数学式，首先只考虑一周的饮料清单，透过 Forward-Backward Algorithm 我们可以求出 αt（i） 和 βt（i），也就是把每一个时间点会经过每一个状态及事件的所有可能路径机率都算出来，求出来之后，自然就要开始训练参数啦！

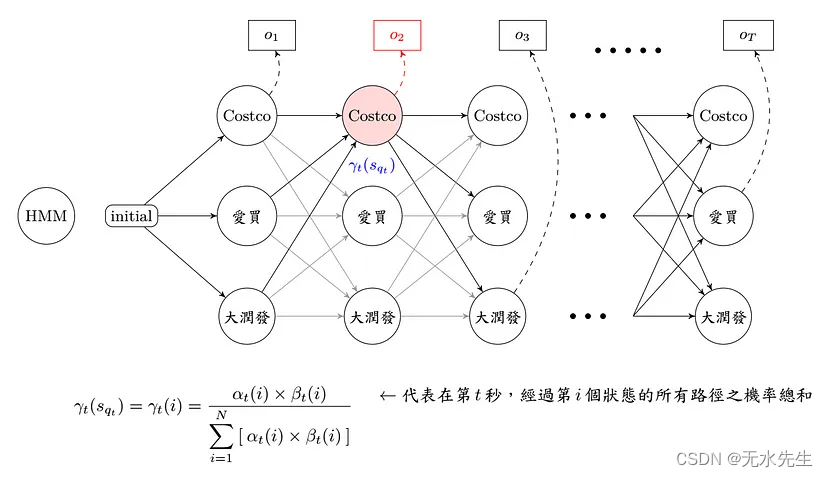
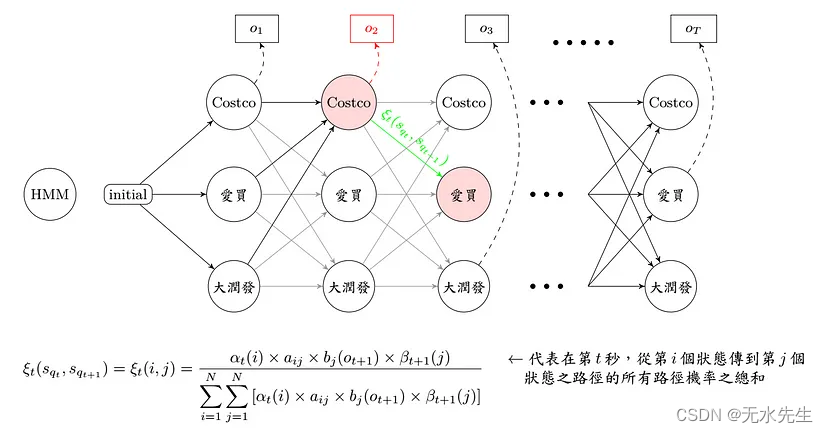
Training 啰！

在标题中看到 EM Algorithm，应该很快就联想到了「分群」、「资料分布」，是的，我们这里处理的手法其实也差不多啦！ 利用事件发生的平均机率，当作更新的转移矩阵，接着反复的寻找和更新，直到更新幅度很小这样。

Comment：

没有出现在数据集中的观察值，在更新的过程中，会被更新为0，一旦变成0，此事件路径发生的可能性即为0，因此不论计算Evaluate Problem或是Decording Problem此路径机率皆恒为0，意思是不会再更新，所以通常不会让没出现过的观察值机率为0，常理来说，会预设一个比0大，但很小的数字。 只有离散问题，会遇到此状况，连续则无。
因为每次的 update，都只与当下计算的观察序列有关，因此很容易看到第 n 个序列的时候，就忘掉一开始看到的几个序列的样子了，为了避免这样的状况产生，所以我们让每次要更新的值，与将要被更新的值取一个比例平衡，既不忘了过去的观察序列，也不会全然依照新的观察序列更新，常用的方式如底下公式…

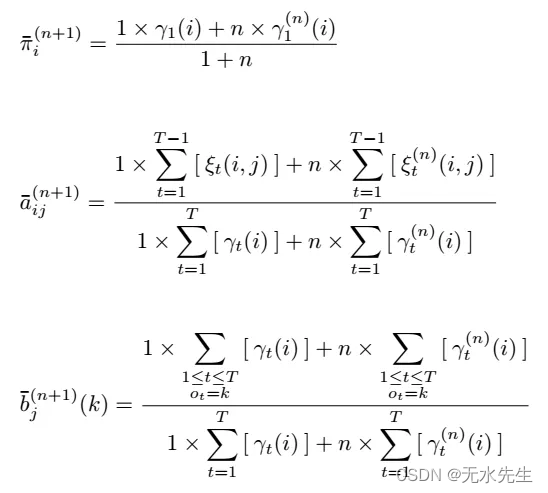
当然有些人会困惑， 之前我们讨论的内容中，每个状态都会有固定对应的 M 个观察值，意思是，原先卖场饮料都是一罐一罐卖的，后来为了环保考量不用铝罐装，用一袋袋饮料装？ 由于是一袋袋的，所以每一袋饮料的重量都有些许的误差，长久下来，观察值会由消费者买了架上第 k 种每瓶为 L ml 的饮料，变成是买了架上第 k 种每袋为 L ml 的饮料，因为不是每袋都能很准确的装刚好 L ml 的饮料，所以会有一点点偏差— 「连续型隐藏式马可夫模型 Continuous Hidden Markov Model」

六、 连续隐马尔可夫

上述的想法，大家思考一下，看到“bias 偏差”大家会想到啥？ 八九不离十，是令人脑昏的“统计”，统计数据会想到啥？ 「常态分布 Normal Distribution」。 没错，不管什么状态，未看先猜有「常态分布」，先对一半。 那什么东西训练中会与「常态分布」有关，眼睛闭着，也猜得到「EM Algorithm」，接着联想到的就是「Gaussian Distribution」、「Gaussian Mixture Model」。 既然有这些联想，那一切就好办了。 让我们走下去…

于是乎我们训练的目标中多了一个参数——在「状态 st」产生「观察值 ot」的机率。 目前我们以 Gaussian Mixture Model 为假设观察值 ot 所属分布，那马上就会想到，多了的训练参数是谁了吧!! 没错，就是「平均数 mean μ」和「变异数 covariance Σ」

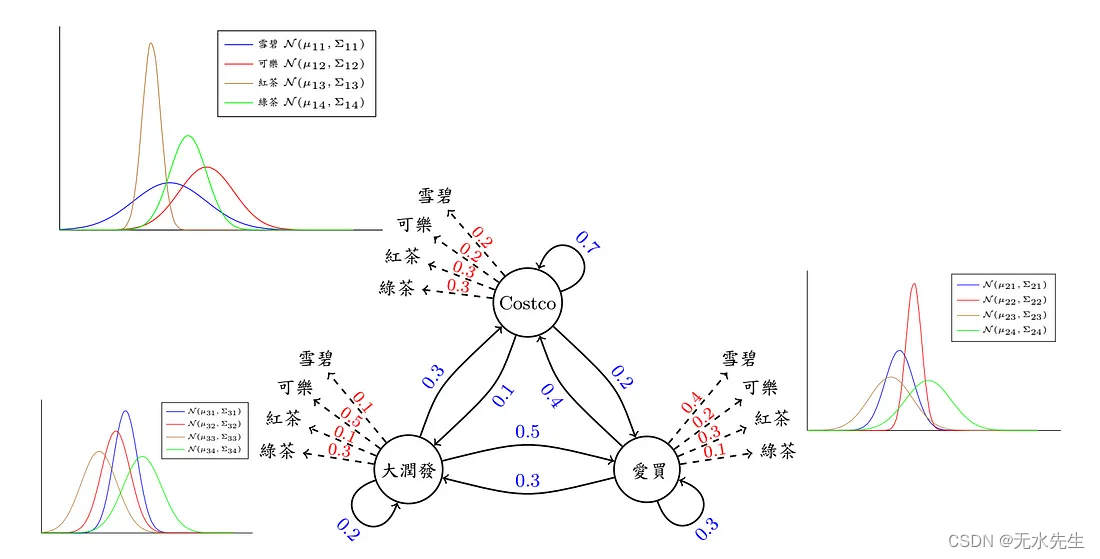
有了这张图，大概就清楚明了了吧！ 简单叙述整个问题，就是…圆仔每天都会去买饮料，所以我们纪录她每天买的饮料品项和饮料重量，然后每 7 天为一笔资料，目的是找出圆仔买东西的习惯和路径，以及买到东西多寡的分析，所以影响的因素和对应的名词有三个「卖场 →状态」、「饮料 →观察」、「饮料重量 →N（ μ， Σ ）」，目标是从这三者中计算出最可能是圆仔的习惯 — — 买东西的路径机率、选择买哪种饮料的机率、得到此饮料重量的机率。

一定会有人觉得紧张该怎么办，其实也不用怎么办啦!! 跟刚刚计算的方法差不多，只是多了要更新「平均值 μ」和「共变异数 Σ」而已

YA！ 我们终于结束 Hidden Markov Model 系列啦!! 给自己一个欢呼吧！ 其实一切都不难，不要看到数学是就害怕了。

Reference：
（1）算法笔记- Hidden Markov Model
（2）Hidden Markov Models — Stanford University