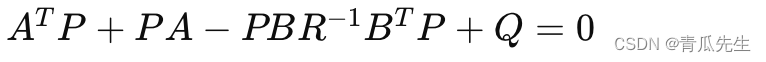一 动画规划的概念 优化出现重复解的递归

一旦写出递归来，改动态规划就很快

尝试策略和状态转移方程是一码事

学会尝试是攻克动态规划最本质的能力

如果你发现你有重复调用的过程，动态规划在算过一次之后把答案记下来，下回在越到重复调用过程就直接调

做题思路 一定要从尝试入手

动态规划的套路从尝试出发,从尝试递归出发，然后在改动态规划的时候第一步找到base的情况填上相应位置的数，然后根据下一步的条件推出其他位置的数；

二 给定四个参数 N、M、K、P，返回方法数，机器人必须走 K 步

2.1描述

假设有排成一行的N个位置，记为1~N，N 一定大于或等于 2

开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)

如果机器人来到1位置，那么下一步只能往右来到2位置；

如果机器人来到N位置，那么下一步只能往左来到 N-1 位置；

如果机器人来到中间位置，那么下一步可以往左走或者往右走；

规定机器人必须走 K 步，最终能来到P位置(P也是1~N中的一个)的方法有多少种

给定四个参数 N、M、K、P，返回方法数。

2.2 分析

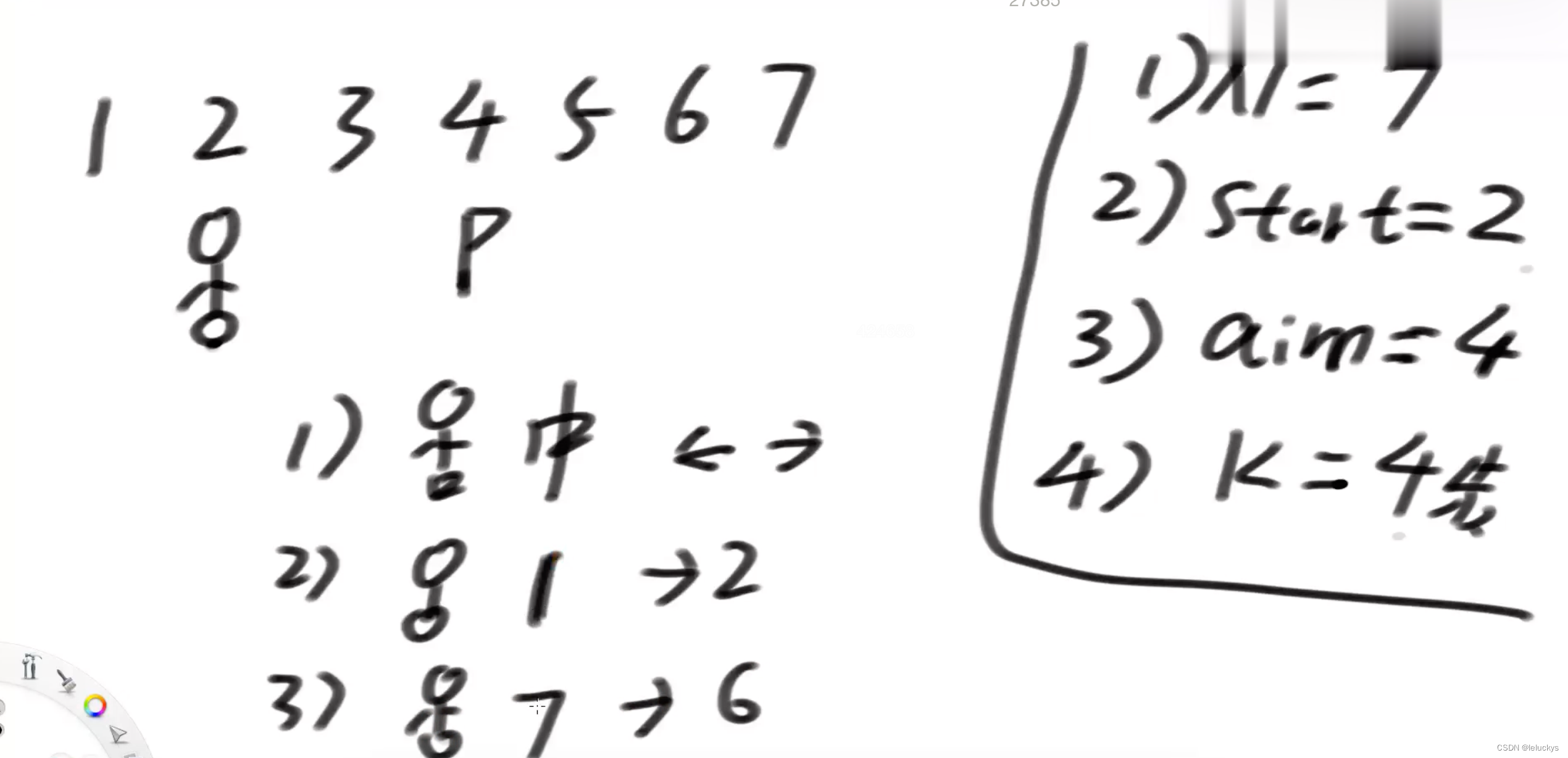
2.3 代码

// 机器人当前来到的位置是cur，// 机器人还有rest步需要去走，// 最终的目标是aim，// 有哪些位置？1~N// 返回：机器人从cur出发，走过rest步之后，最终停在aim的方法数，是多少？public static int process1(int cur, int rest, int aim, int N) {if (rest == 0) { // 如果已经不需要走了，走完了！return cur == aim ? 1 : 0;}// (cur, rest)if (cur == 1) { // 1 -> 2return process1(2, rest - 1, aim, N);}// (cur, rest)if (cur == N) { // N-1 <- Nreturn process1(N - 1, rest - 1, aim, N);}// (cur, rest)return process1(cur - 1, rest - 1, aim, N) + process1(cur + 1, rest - 1, aim, N);}

2.4 优化 递归改动态规划 一 有重复解的递归是可以优化的

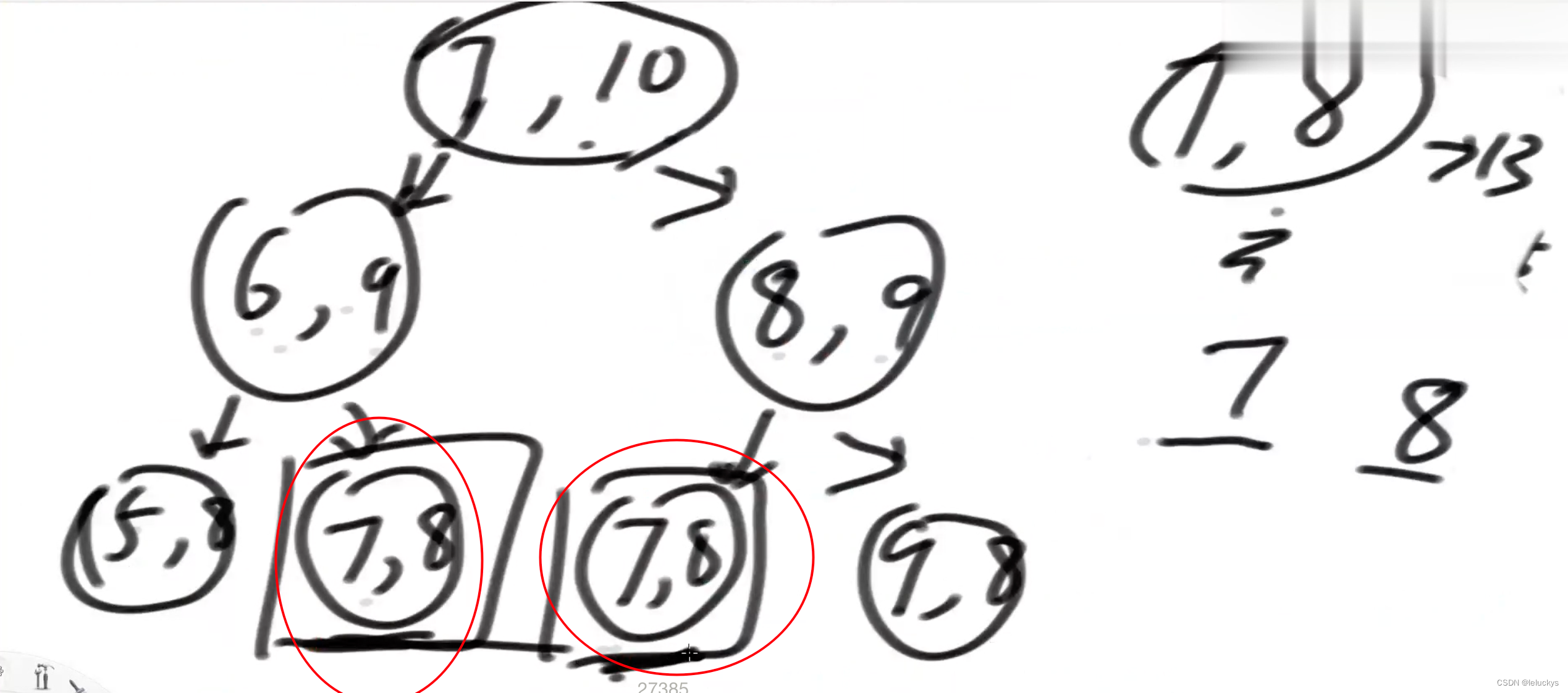
上面递归的过程中出现了重复的值，采用缓存法记录已经走过的路就不用再走了，一个字问题保证只算一次

public static int ways2(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}int[][] dp = new int[N + 1][K + 1];for (int i = 0; i <= N; i++) {for (int j = 0; j <= K; j++) {dp[i][j] = -1;}}// dp就是缓存表// dp[cur][rest] == -1 -> process1(cur, rest)之前没算过！// dp[cur][rest] != -1 -> process1(cur, rest)之前算过！返回值，dp[cur][rest]// N+1 * K+1return process2(start, K, aim, N, dp);}// cur 范: 1 ~ N// rest 范：0 ~ Kpublic static int process2(int cur, int rest, int aim, int N, int[][] dp) {if (dp[cur][rest] != -1) {return dp[cur][rest];}// 之前没算过！int ans = 0;if (rest == 0) {ans = cur == aim ? 1 : 0;} else if (cur == 1) {ans = process2(2, rest - 1, aim, N, dp);} else if (cur == N) {ans = process2(N - 1, rest - 1, aim, N, dp);} else {ans = process2(cur - 1, rest - 1, aim, N, dp) + process2(cur + 1, rest - 1, aim, N, dp);}dp[cur][rest] = ans;return ans;}

三 给定一个整型数组arr，代表数值不同的纸牌排成一条线

范围模型 玩家博弈问题

3.1 描述

给定一个整型数组arr，代表数值不同的纸牌排成一条线

玩家A和玩家B依次拿走每张纸牌

规定玩家A先拿，玩家B后拿

但是每个玩家每次只能拿走最左或最右的纸牌

玩家A和玩家B都绝顶聪明

请返回最后获胜者的分数。

3.2分析

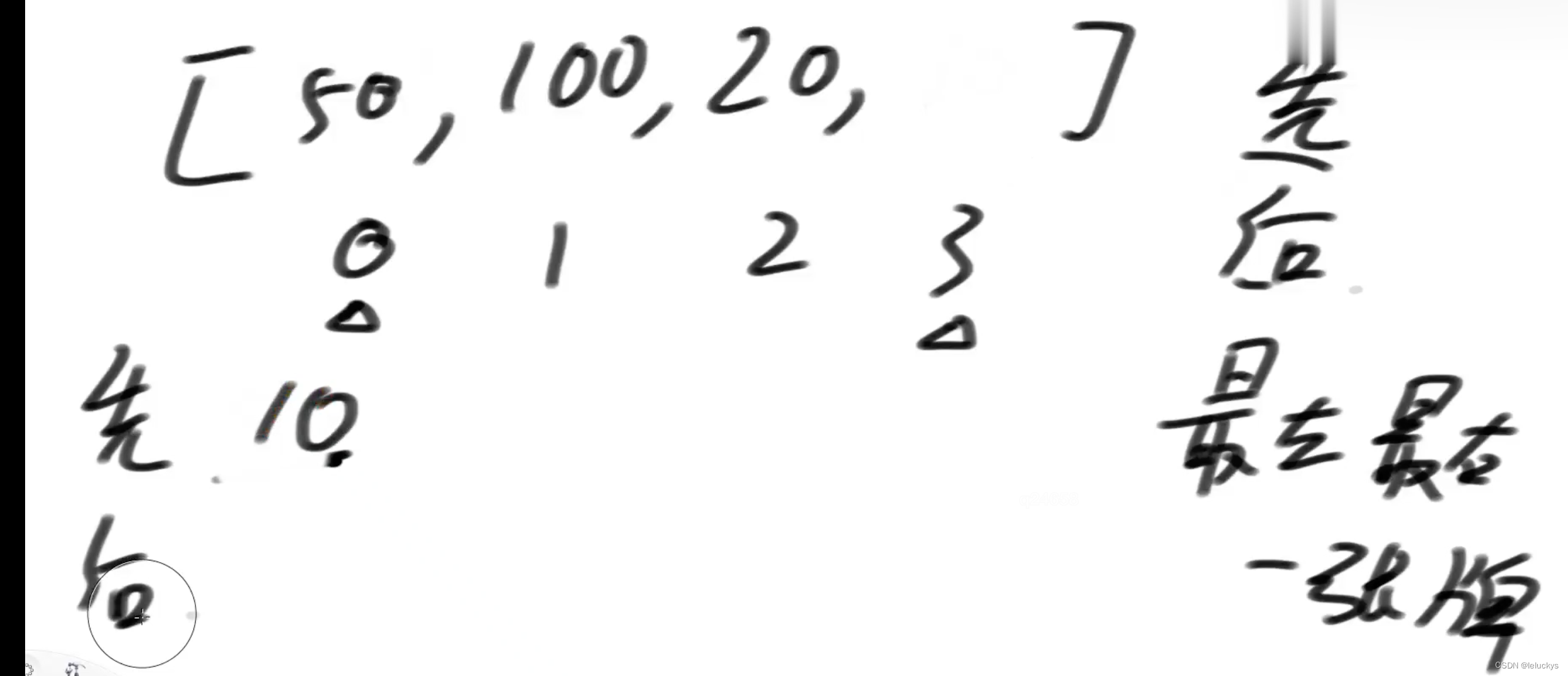
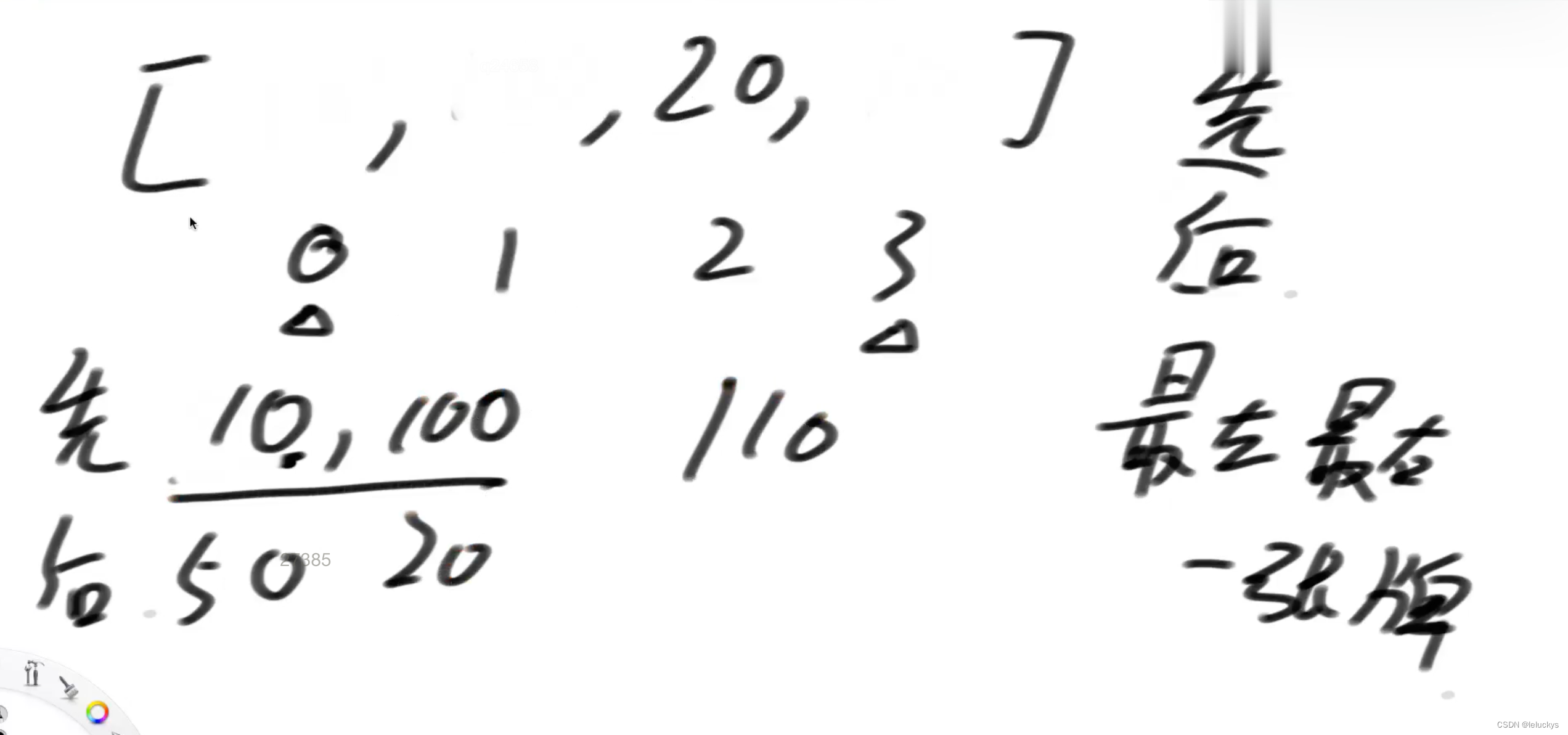
先手

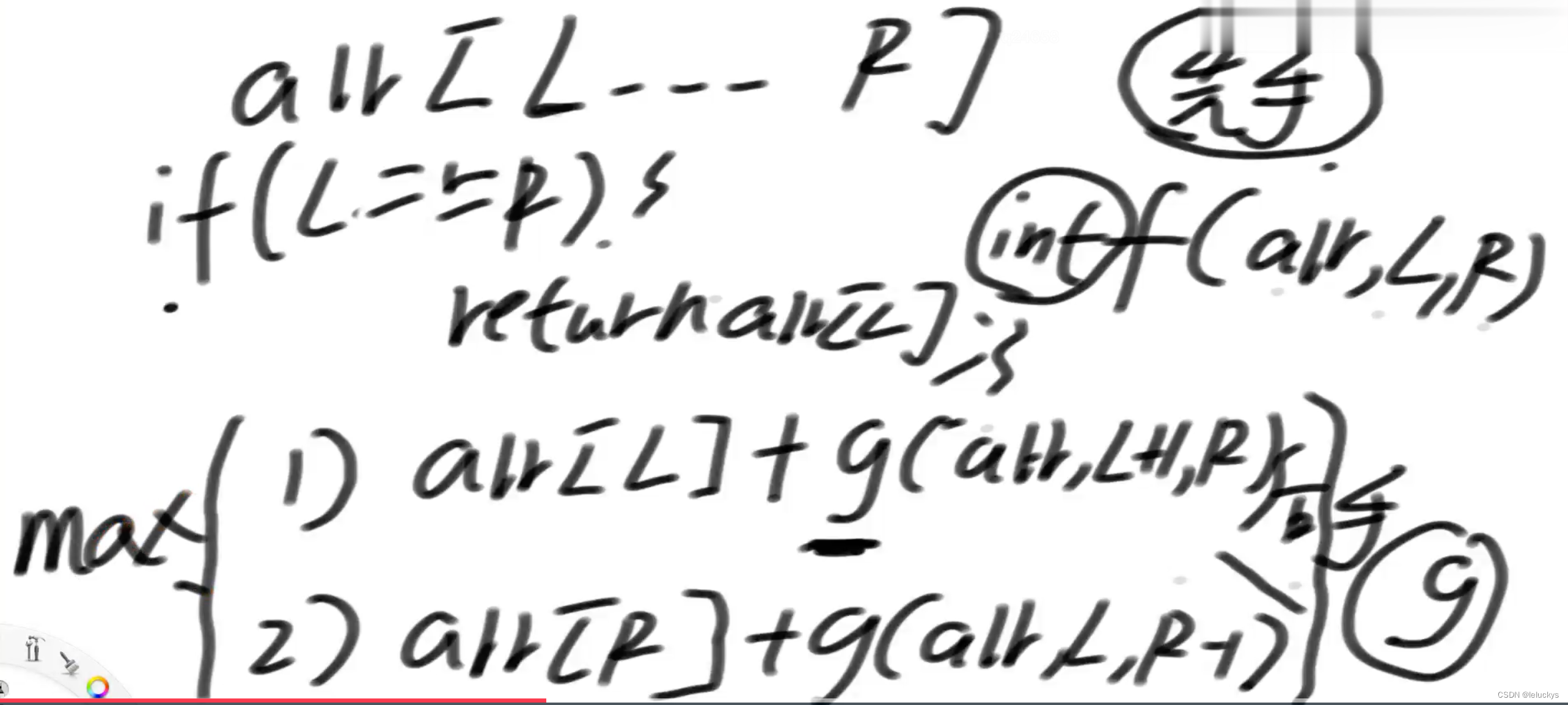
后手，后手能拿的只能是先手拿剩下的

优化1 傻缓存

优化二

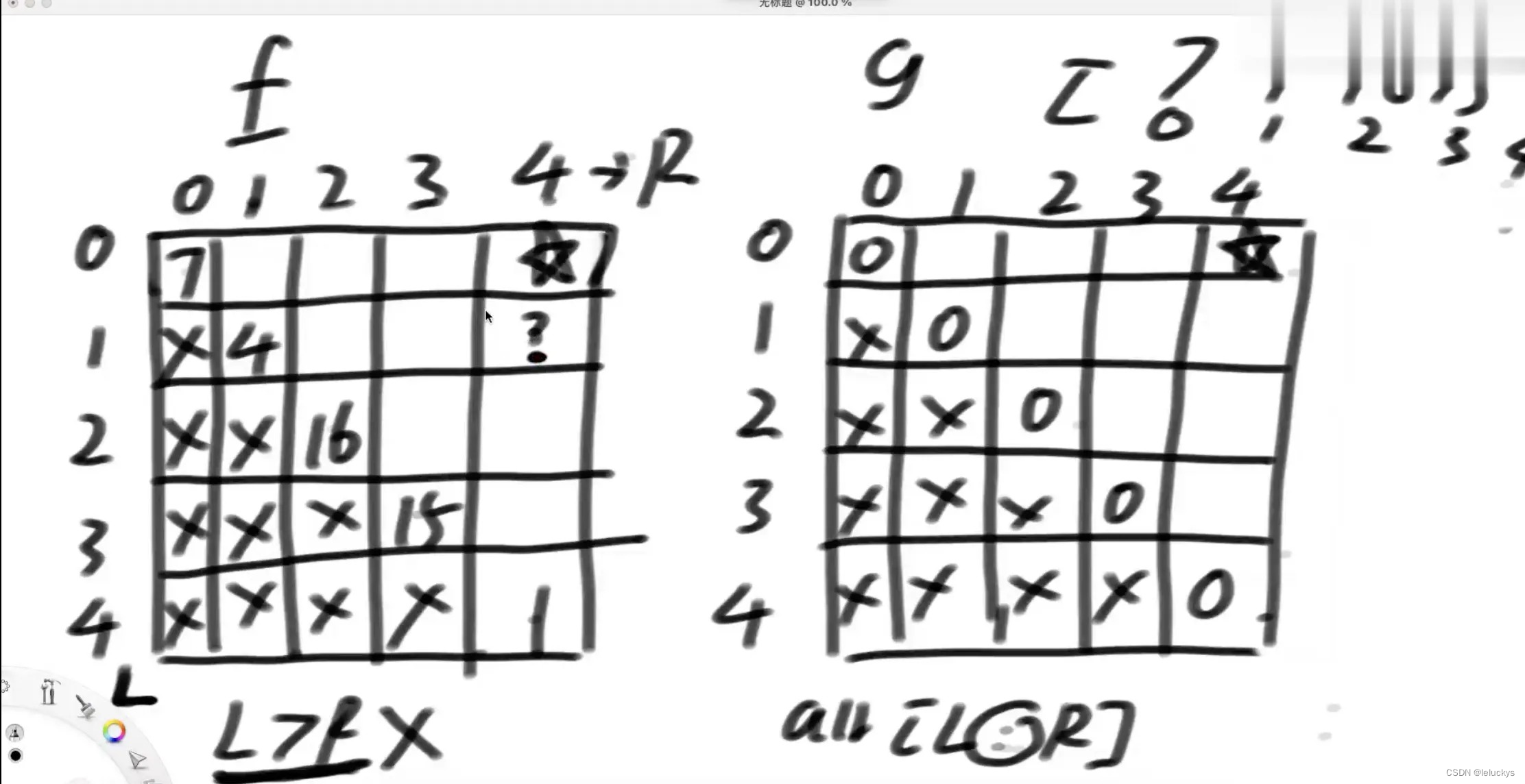
3.3代码

package class18;public class Code02_CardsInLine {// 根据规则，返回获胜者的分数public static int win1(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int first = f1(arr, 0, arr.length - 1);int second = g1(arr, 0, arr.length - 1);return Math.max(first, second);}// arr[L..R]，先手获得的最好分数返回public static int f1(int[] arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g1(arr, L + 1, R);int p2 = arr[R] + g1(arr, L, R - 1);return Math.max(p1, p2);}// // arr[L..R]，这里面是对手做决定，后手获得的最好分数返回public static int g1(int[] arr, int L, int R) {if (L == R) {return 0;}int p1 = f1(arr, L + 1, R); // 对手拿走了L位置的数int p2 = f1(arr, L, R - 1); // 对手拿走了R位置的数return Math.min(p1, p2);}public static int win2(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {fmap[i][j] = -1;gmap[i][j] = -1;}}int first = f2(arr, 0, arr.length - 1, fmap, gmap);int second = g2(arr, 0, arr.length - 1, fmap, gmap);return Math.max(first, second);}// arr[L..R]，先手获得的最好分数返回public static int f2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R) {ans = arr[L];} else {int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);ans = Math.max(p1, p2);}fmap[L][R] = ans;return ans;}// // arr[L..R]，后手获得的最好分数返回public static int g2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (gmap[L][R] != -1) {return gmap[L][R];}int ans = 0;if (L != R) {int p1 = f2(arr, L + 1, R, fmap, gmap); // 对手拿走了L位置的数int p2 = f2(arr, L, R - 1, fmap, gmap); // 对手拿走了R位置的数ans = Math.min(p1, p2);}gmap[L][R] = ans;return ans;}

3.4 优化代码

 public static int win3(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}return Math.max(fmap[0][N - 1], gmap[0][N - 1]);}public static void main(String[] args) {int[] arr = { 5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7 };System.out.println(win1(arr));System.out.println(win2(arr));System.out.println(win3(arr));}}