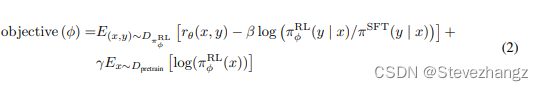给定当前优化的大模型 π \pi π,以及SFT模型 π S F T \pi_{SFT} πSFT
原始优化目标为: max E ( s , a ) ∼ R L [ π ( s , a ) π S F T ( s , a ) A π S F T ( s , a ) ] \max E_{(s,a)\sim RL}[\frac{\pi(s,a)}{\pi_{SFT}(s,a)}A^{\pi_{SFT}}(s,a)] maxE(s,a)∼RL[πSFT(s,a)π(s,a)AπSFT(s,a)]
假设型 π \pi π,以及SFT模型 π S F T \pi_{SFT} πSFT的KL散度很小即 π ( s , a ) π S F T ( s , a ) = 1 \frac{\pi(s,a)}{\pi_{SFT}(s,a)}=1 πSFT(s,a)π(s,a)=1
给定奖励模型 r ( s , a ) ∈ [ 0 , 1 ] r(s,a)\in [0,1] r(s,a)∈[0,1],
假设整个事件的时间范围就1步所以 Q ( s , a ) = R ( s , a ) = r ( s , a ) Q(s,a)=R(s,a)=r(s,a) Q(s,a)=R(s,a)=r(s,a)
可以得到:
max E ( s , a ) ∼ R L [ π ( s , a ) π S F T ( a ∣ s ) A π S F T ( a ∣ s ) ] = max E ( s , a ) ∼ R L [ π ( a ∣ s ) π S F T ( a ∣ s ) ( Q π S F T ( s , a ) − V π S F T ( s ) ) ] = max E ( s , a ) ∼ R L [ π ( a ∣ s ) π S F T ( a ∣ s ) ( r ( s , a ) − V π S F T ( s ) ) ] = max E ( s , a ) ∼ R L [ r ( s , a ) − π ( a ∣ s ) π S F T ( a ∣ s ) V π S F T ( s ) ] = max E ( s , a ) ∼ R L [ r ( s , a ) − π ( a ∣ s ) π S F T ( a ∣ s ) ∫ a Q π S F T ( s , a ) ] = max E ( s , a ) ∼ R L [ r ( s , a ) − π ( a ∣ s ) π S F T ( a ∣ s ) ∫ a r ( s , a ) ] = max E ( s , a ) ∼ R L [ r ( s , a ) − π ( a ∣ s ) π S F T ( a ∣ s ) ] \max E_{(s,a)\sim RL}[\frac{\pi(s,a)}{\pi_{SFT}(a|s)}A^{\pi_{SFT}}(a|s)] \\=\max E_{(s,a)\sim RL}[\frac{\pi(a|s)}{\pi_{SFT}(a|s)}(Q^{\pi_{SFT}}(s,a)-V^{\pi_{SFT}}(s))]\\=\max E_{(s,a)\sim RL}[\frac{\pi(a|s)}{\pi_{SFT}(a|s)}(r(s,a)-V^{\pi_{SFT}}(s))]\\=\max E_{(s,a)\sim RL}[r(s,a)-\frac{\pi(a|s)}{\pi_{SFT}(a|s)} V^{\pi_{SFT}}(s)]\\=\max E_{(s,a)\sim RL}[r(s,a)-\frac{\pi(a|s)}{\pi_{SFT}(a|s)}\int_{a} Q^{\pi_{SFT}}(s,a)]\\=\max E_{(s,a)\sim RL}[r(s,a)-\frac{\pi(a|s)}{\pi_{SFT}(a|s)}\int_{a} r(s,a)]\\=\max E_{(s,a)\sim RL}[r(s,a)-\frac{\pi(a|s)}{\pi_{SFT}(a|s)}] maxE(s,a)∼RL[πSFT(a∣s)π(s,a)AπSFT(a∣s)]=maxE(s,a)∼RL[πSFT(a∣s)π(a∣s)(QπSFT(s,a)−VπSFT(s))]=maxE(s,a)∼RL[πSFT(a∣s)π(a∣s)(r(s,a)−VπSFT(s))]=maxE(s,a)∼RL[r(s,a)−πSFT(a∣s)π(a∣s)VπSFT(s)]=maxE(s,a)∼RL[r(s,a)−πSFT(a∣s)π(a∣s)∫aQπSFT(s,a)]=maxE(s,a)∼RL[r(s,a)−πSFT(a∣s)π(a∣s)∫ar(s,a)]=maxE(s,a)∼RL[r(s,a)−πSFT(a∣s)π(a∣s)]
此外为了约束模型 π \pi π和 π S F T \pi_{SFT} πSFT之间不要差得太远还需要使用SFT的数据训练 π \pi π,等价于 max E ( s , a ) ∼ π S F T [ π ( a ∣ s ) ] \max E_{(s,a)\sim \pi_{SFT}}[\pi(a|s)] maxE(s,a)∼πSFT[π(a∣s)]。因此优化目标就变成了:
max E ( s , a ) ∼ R L [ r ( s , a ) − π ( a ∣ s ) π S F T ( a ∣ s ) ] + E ( s , a ) ∼ π S F T [ π ( a ∣ s ) ] \max E_{(s,a)\sim RL}[r(s,a)-\frac{\pi(a|s)}{\pi_{SFT}(a|s)}]+E_{(s,a)\sim \pi_{SFT}}[\pi(a|s)] maxE(s,a)∼RL[r(s,a)−πSFT(a∣s)π(a∣s)]+E(s,a)∼πSFT[π(a∣s)]
这一项和GPT3.5的优化目标基本一致: