在理解神经网络的可学习性之前,需要先从数学中的导数、数值微分、偏导数、梯度等概念入手,从而理解为什么神经网络具备学习能力。
1.数值微分的定义
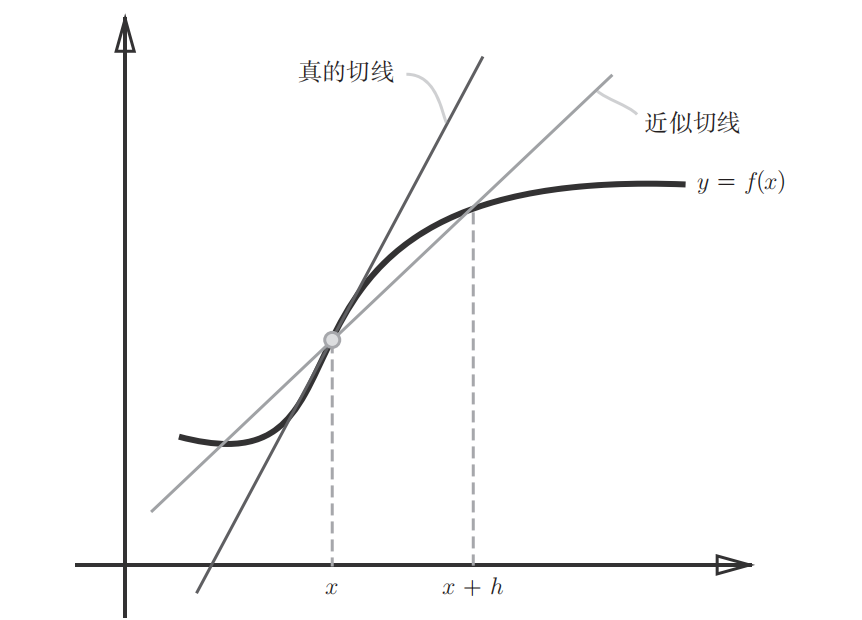
先从导数出发理解什么是梯度。某一点的导数直观理解就是在该点的切线的斜率。在数学中导数表示某个瞬时的变化量,如下公式表示:

上述利用微小的差分求导数的过程称为数值微分(numerical differentiation),公式(1)表示的是前向差分(f(x+h)-f(x)),因为h无法无限趋近于0,所以存在误差(如下图所示)。为了减小这种数值微分误差,可以用中心差分(f(x+h)-f(x-h))减小误差。
2.数值微分的例子
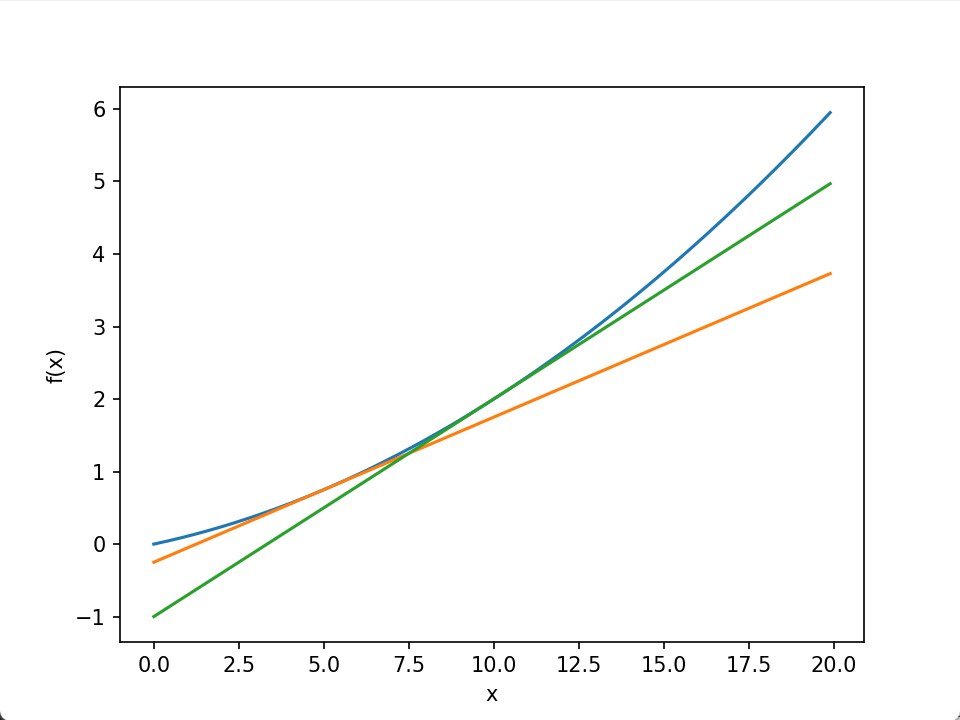
以下面这个二次函数为例,对其数在x = 5和x = 10处进行求导。

import numpy as np
import matplotlib.pylab as pltdef numerical_diff(f, x):h = 1e-4 # 0.0001return (f(x+h) - f(x-h)) / (2*h) # 中心差分def function_1(x):return 0.01*x**2 + 0.1*x def tangent_line(f, x):d = numerical_diff(f, x)print(d) # 0.1999999999990898 0.2999999999986347y = f(x) - d*xreturn lambda t: d*t + y#该函数首先调用numerical_diff函数来计算函数f在点x处的导数d,然后根据切线的方程 y = ax + b 中的斜率和截距来计算切线的斜率d和截距y。最后返回一个匿名函数,该函数接受一个参数 t,并返回切线上在 t 处的函数值。
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")tf1 = tangent_line(function_1, 5) # x=5处的切线方程
tf2 = tangent_line(function_1, 10) # x=10处的切方程
y1 = tf1(x)
y2 = tf2(x)plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.show()
3.偏导数和梯度
下式表示的是包含两个变量的函数,可以看为计算平面内点的坐标的平方和函数:

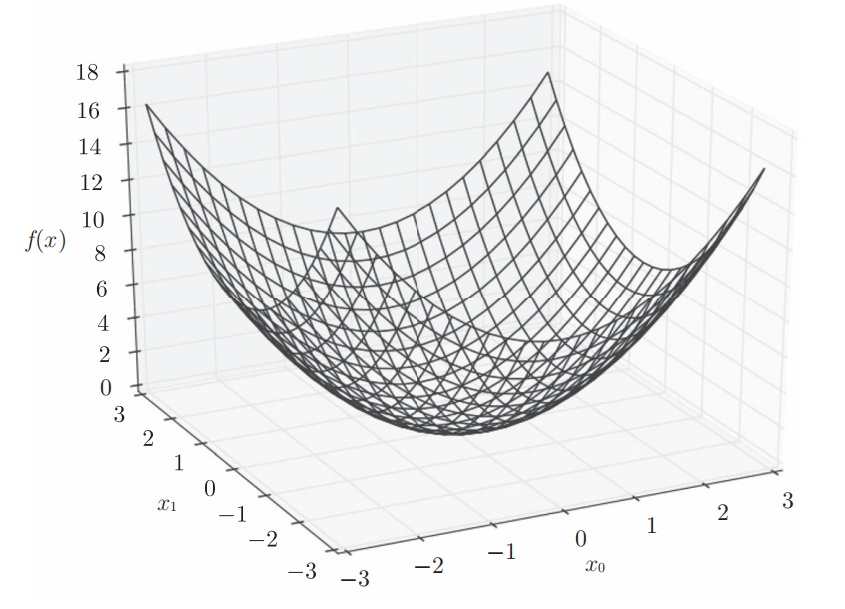
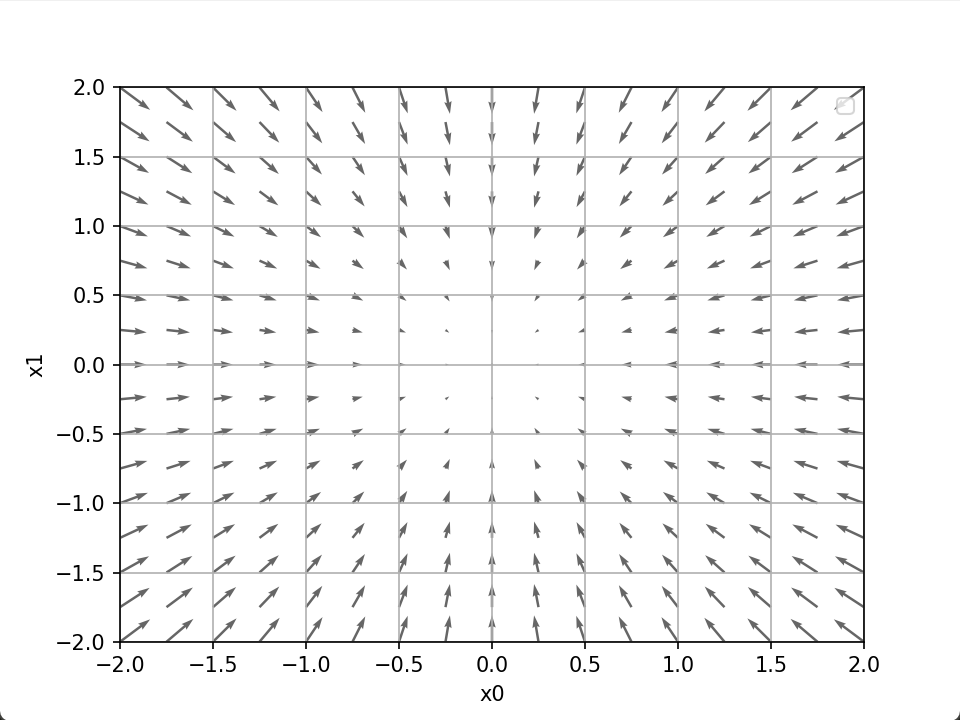
求某个变量的偏导数时,需要将多个变量中的某一个变量定为目标变量,并将其他变量固定为某个值才能求解。下面是该函数(由全部变量的偏导数汇总而成的向量)梯度(gradient)的可视化。
4.梯度法
机器学习的主要任务是在学习时寻找最优参数,而神经网络也必须在学习时找到最优的参数(权重和偏置)。上面介绍的函数其梯度指向的是函数最小值的方向,但是在复杂函数也就是一般的情况下,梯度下降的方向不一定是指向函数最小值,因为还可能存在鞍点(极小值、局部极值)。一般来说,损失函数很复杂,参数空间庞大,不知道它在何处能取得最小值,因此可以利用梯度求最小值。梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法。其中寻找最小值的梯度法称为梯度下降法,寻找最大值的梯度法称为梯度上升法。一般情况下,在神经网络中主要指的是梯度下降法,要最小化损失函数,最终得到最小值处对应的神经网络的权重和偏置,此时神经网络就被训练好了。
def gradient_descent(f, init_x, lr=0.01, step_num=100):x = init_xfor i in range(step_num):grad = numerical_gradient(f, x)x -= lr * gradreturn xdef function_2(x):return x[0]**2 + x[1]**2init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100) # 得到损失函数最小值对应的坐标点(0, 0),array([ -6.11110793e-10, 8.14814391e-10])
f是要进行最优化的函数,,init_x是初始值,lr是学习率learning rate,step_num是梯度法的重复次数。在上面的例子中,学习率设置为0.1。学习率设置的过大或过小对于损失函数的收敛都不利,因此选取合适的学习率也是神经网络超参数的一个重要部分。与神经网络的权重和偏置不同,学习率需要人为设定。如何理解学习率过大过小对损失函数收敛的影响呢?现在我们将损失函数想象成一口大铁锅,锅底的位置就是损失函数达到最小值的地方。当学习率设置的过小时,此时可以看成是放了一只小蚂蚁在锅的外边缘,步子很小,它需要走很多步才能走到底部,耗时长且效率慢,而且有可能陷入“局部最优”。而学习率过大则可以想象成是跳蚤,它每次向前运动的幅度很大,仅略小于锅的尺寸,它会在锅的侧壁来回弹跳,而到达不了锅底。
5.神经网络的梯度
神经网络在学习的过程中也要进行梯度的计算。以一个只有一个形状为2 × 3的权重W的神经网络为例,它的损失函数用L表示,那么梯度

可表示为如下:

求梯度代码实现:
import sys, os
import numpy as npdef softmax(x):if x.ndim == 2:x = x.Tx = x - np.max(x, axis=0)y = np.exp(x) / np.sum(np.exp(x), axis=0)return y.T x = x - np.max(x) # 溢出对策return np.exp(x) / np.sum(np.exp(x))def cross_entropy_error(y, t):if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引if t.size == y.size:t = t.argmax(axis=1)batch_size = y.shape[0]return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_sizedef numerical_gradient(f, x):h = 1e-4 # 0.0001grad = np.zeros_like(x)it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])while not it.finished:idx = it.multi_indextmp_val = x[idx]x[idx] = float(tmp_val) + hfxh1 = f(x) # f(x+h)x[idx] = tmp_val - h fxh2 = f(x) # f(x-h)grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值it.iternext() return gradclass simpleNet:def __init__(self):self.W = np.random.randn(2,3)def predict(self, x):return np.dot(x, self.W)def loss(self, x, t):z = self.predict(x)y = softmax(z)loss = cross_entropy_error(y, t)return lossx = np.array([0.6, 0.9])
t = np.array([0, 0, 1])net = simpleNet()f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)print(dW)
结果:

6.神经网络学习的实现流程
完整实现参见《深度学习入门:基于python的理论与实现》第四章第五节的内容。以上是神经网路学习的所有基本概念,包括“mini-batch”、“梯度”、“梯度下降法”等概念。神经网络的学习过程为:
前提:训练数据是均匀的,即是被shuffle(打乱)过的。其次神经网络已经存在较为合适的权重和偏置。
step1:按照mini-batch的方法从训练数据中随机选出一部分数据进行训练。
step2:计算各个权重参数的梯度,梯度表示函数值减小最多的方向。
step3:将权重参数沿梯度方向进行微小更新(lr,学习率)。
step4:重复 step1、step2、step3。
上面使用的数据时从原始数据中随机选择的mini-batch数据,所以又称之为随机梯度下降法(stochastic gradient descent),即对随机选择的数据进行的梯度下降法。在很多深度学习框架中,其一般由一个名为SGD的函数进行实现。为了保证所有的训练数据都被使用,一般做法是事先将所有训练数据随机打乱,然后按指定的批次大小按序生成mini-batch。这样每个mini-batch均有一个索引号,然后用索引号可以遍历所有的mini-batch。遍历一次所有数据,就称为一个epoch。