本文使用数据来源自2023年数学建模国赛C题,以附件1、附件2数据为基础,通过excel的数据透视表等功能重新汇总了一份新的数据表,从中截取了一部分数据为例用于绘制图表。绘制的图表包括一维直方图、一维核密度估计图、二维直方图、二维核密度估计图、箱线图、累计分布函数图。
本文为原创,初稿发布至博客园,网址:https://www.cnblogs.com/-zyr/p/17841061.html,如有转载请标注来源,谢谢!
一.一维直方图和核密度估计图
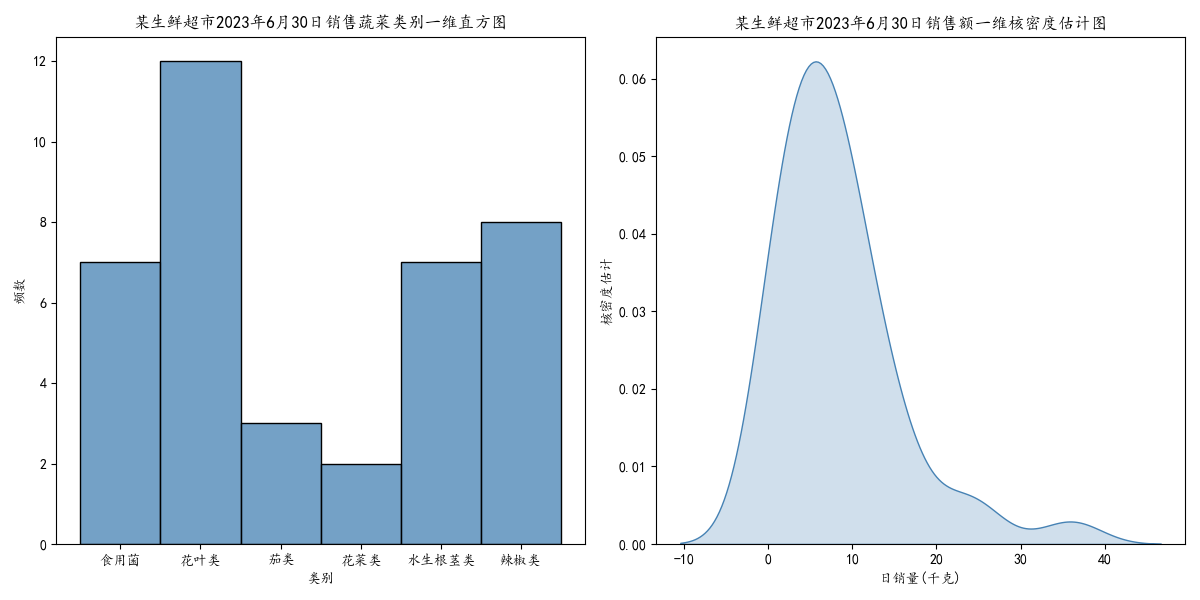
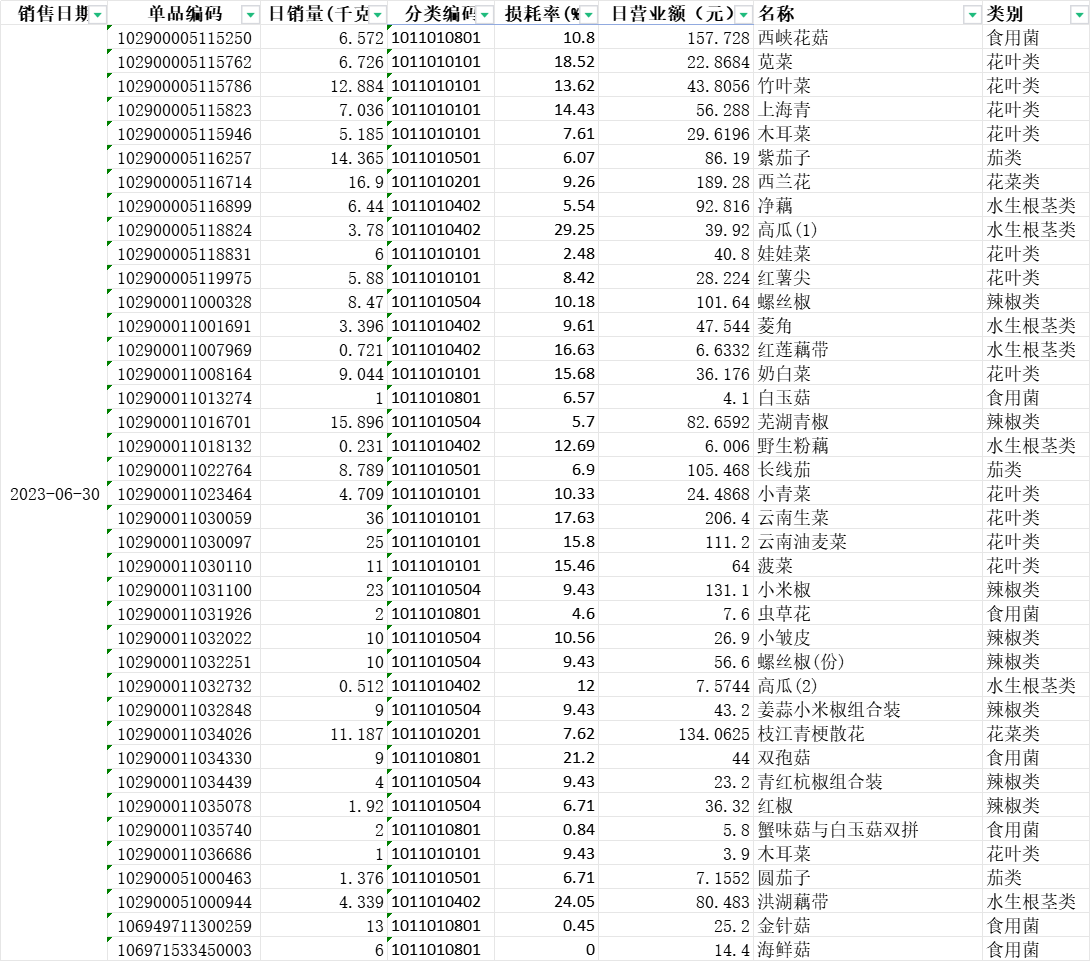
以某生鲜超市2023年6月30日销售流水数据为基础,整理出当日的各类商品销售情况表(如4.附件:数据的图所示),绘制了蔬菜类别的一维直方图、日销量的一维核密度估计图。核密度估计图可以反映了销售量较为集中的范围。
代码步骤如下:
①从Excel文件中读取名为"2023-6-30日销售情况"的工作表数据
②从表中提取损耗率、日销量和类别等关键列的数据
③利用seaborn和matplotlib绘制了一个包含两个子图的图形,分别是:
蔬菜类别的一维直方图,显示每个类别的销售频数
日销量的一维核密度估计图,显示销售额的分布情况
⑥设置了图形的标签、标题和布局,确保图形的可读性和美观性,通过plt.show()显示生成的图形
关键函数:
①seaborn.histplot(data, bins=20, kde=False, color=‘steelblue’) # 绘制一维直方图
seaborn.histplot() 用于绘制一维直方图,直方图是一种对数据分布进行粗略估计的图形表示。它将数据范围划分为一系列连续的区间,然后统计每个区间内数据点的数量,并将这些数量用柱状图表示。通过直方图,可以直观地看到数据的分布情况,了解数据集中的集中趋势、离散程度等信息
data:要绘制的数据,可以是 Pandas DataFrame、NumPy 数组或其他类似的数据结构。bins:指定直方图的箱子数量,或者是箱子的边缘位置。可以是一个整数,表示箱子的数量,也可以是一个表示箱子边缘位置的序列。默认值为 `auto`,由 Seaborn 根据数据自动选择
kde:一个布尔值,表示是否在直方图上叠加核密度估计。默认为 False。
color:指定直方图的颜色。可以是字符串(表示颜色的名称)、元组(表示 RGB 值)或其他有效的颜色表示方式。
详细参数可见官方文档:seaborn.histplot — seaborn 0.13.0 documentation (pydata.org)
②seaborn.kdeplot(data, fill=True, color=‘steelblue’)#绘制一维核密度图
seaborn.kdeplot()用于绘制一维核密度图,核密度图是通过对数据进行平滑处理,估计概率密度函数的图形表示。核密度图可以提供更加平滑的数据分布估计,相比直方图,它对数据的分布进行了更加连续的建模。
data:要绘制的数据,可以是 Pandas DataFrame、NumPy 数组或其他类似的数据结构
fill:一个布尔值,表示是否填充核密度图下方的区域。如果为 True,则填充;如果为 False,则只绘制轮廓线。默认为 True
color:指定核密度图的颜色。可以是字符串(表示颜色的名称)、元组(表示 RGB 值)或其他有效的颜色表示方式。
代码:
1 import pandas as pd 2 import matplotlib.pyplot as plt 3 import seaborn as sns # matplotlib的补充4 5 # 读取Excel文件6 file\_path = "单日销售情况.xlsx"7 sheet\_name = "2023-6-30日销售情况"8 df = pd.read\_excel(file\_path, sheet\_name) 9
10 # 提取所需的列
11 selected\_columns = \['损耗率(%)', '日销量(千克)', '类别'\]
12 selected\_data = df\[selected\_columns\]
13
14 # 设置显示中文
15 plt.rcParams\['font.sans-serif'\] = \['KaiTi'\] # 'SimHei'也可以
16 plt.rcParams\['axes.unicode\_minus'\] = False
17
18 # 绘制一维直方图
19 plt.figure(figsize=(12, 6))
20 plt.subplot(1, 2, 1)
21 sns.histplot(selected\_data\['类别'\], bins=20, kde=False, color='steelblue')
22 plt.xlabel('类别')
23 plt.ylabel('频数')
24 plt.title('某生鲜超市2023年6月30日销售蔬菜类别一维直方图')
25
26 # 绘制一维核密度估计图
27 plt.subplot(1, 2, 2)
28 sns.kdeplot(x=selected\_data\['日销量(千克)'\], fill=True, color='steelblue')
29 plt.xlabel('日销量(千克)')
30 plt.ylabel('核密度估计')
31 plt.title('某生鲜超市2023年6月30日销售额一维核密度估计图')
32
33 # 显示图形
34 plt.tight\_layout()
35 plt.show()
二.二维统计直方图和核密度估计图
以某生鲜超市2023年6月30日销售流水数据为基础,整理出当日的各类商品销售情况表,绘制了某生鲜超市2023年6月30日39种商品的日销量和损耗率的二维统计直方图和二维核密度估计图。

关键步骤:
①读取数据:从Excel文件中读取了名为"2023-6-30日销售情况"的工作表的数据。
②提取所需列:从数据中提取了’损耗率(%)'和’日销量(千克)'两列数据。
③设置图形参数:设置了中文显示和防止负号显示问题的参数。
④绘制统计直方图和核密度估计图:利用matplotlib和seaborn绘制了一个包含两个子图的图形。左侧子图是二维直方图,表示了日销量和损耗率之间的关系;右侧子图是核密度估计图,展示了这两个变量的分布情况。
⑤显示图形:利用plt.show()将图形显示出来。
关键函数:
①plt.hist2d(x=selected_data[‘日销量(千克)’],y=selected_data[‘损耗率(%)’],bins=(50,50),cmap=‘Blues’):
该函数用于绘制二维直方图,其中x和y分别为数据的两个维度横轴和纵轴,bins参数指定了直方图的箱体数量,cmap参数指定了颜色映射。
②sns.kdeplot(x=selected_data[‘日销量(千克)’],y=selected_data[‘损耗率(%)’],cmap=‘Blues’,fill=True):
该函数用于绘制核密度估计图,其中x和y分别为数据的两个维度,cmap参数指定了颜色映射,fill=True表示使用颜色填充密度曲线下面的区域。
代码:
1 import pandas as pd 2 import matplotlib.pyplot as plt 3 import seaborn as sns # matplotlib的补充4 5 # 读取Excel文件6 file\_path = "单日销售情况.xlsx"7 sheet\_name = "2023-6-30日销售情况"8 df = pd.read\_excel(file\_path, sheet\_name) 9
10 # 提取所需的列
11 selected\_columns = \['损耗率(%)', '日销量(千克)'\]
12 selected\_data = df\[selected\_columns\]
13
14 # 设置显示中文
15 plt.rcParams\['font.sans-serif'\] = \['KaiTi'\] # 'SimHei'也可以
16 plt.rcParams\['axes.unicode\_minus'\] = False
17
18 # 绘制统计直方图和核密度估计图
19 plt.figure(figsize=(12, 6))
20
21 # 绘制二维直方图
22 plt.subplot(1, 2, 1)
23 plt.hist2d(x=selected\_data\['日销量(千克)'\], y=selected\_data\['损耗率(%)'\], bins=(50, 50), cmap='Blues')
24 plt.xlabel('日销量(千克)')
25 plt.ylabel('损耗率(%)')
26 plt.title('某生鲜超市2023年6月30日39种商品日销量和损耗率直方图')
27
28
29 # 绘制核密度估计图
30 plt.subplot(1, 2, 2)
31 sns.kdeplot(x=selected\_data\['日销量(千克)'\], y=selected\_data\['损耗率(%)'\], cmap='Blues', fill=True)
32 plt.xlabel('日销量(千克)')
33 plt.ylabel('损耗率(%)')
34 plt.title('某生鲜超市2023年6月30日39种商品日销量和损耗率核密度估计图')
35
36 # 显示图形
37 plt.tight\_layout()
38 plt.show()
三.箱线图、累积分布函数图
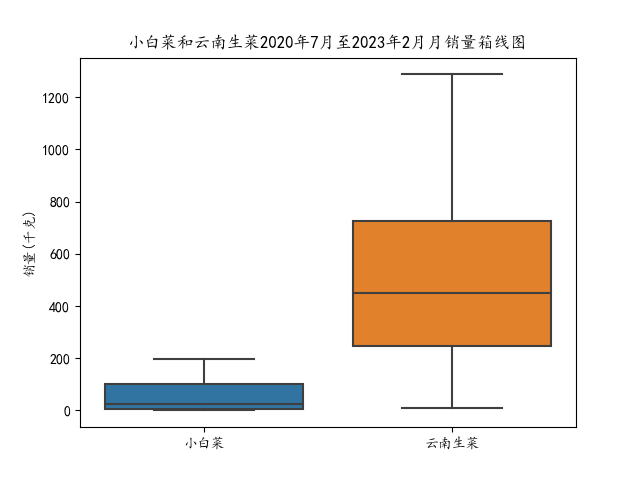
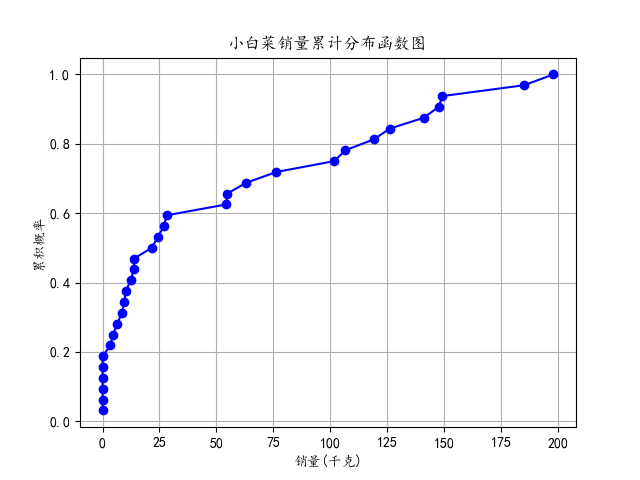
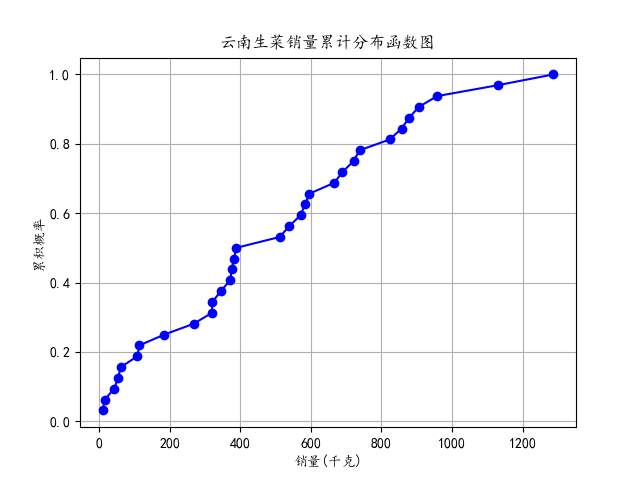
常见的数据分布图表有直方图、核密度估计图、箱线图、散点图、累积分布函数图等,本部分以某生鲜超市2020年7月-2023年2月销售流水数据为基础,整理出小白菜和云南生菜的月销量,绘制箱线图、累积分布函数图,通过箱线图和累积分布函数图分别展示了不同蔬菜销售量的总体分布和累积概率分布情况。
箱线图,又称为盒须图、箱型图,是一种用于显示数据分布情况的统计图表。它能够展示一组或多组数据的中位数、四分位数、最小值、最大值以及可能的异常值
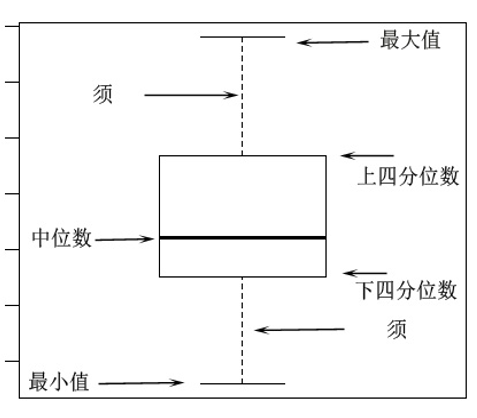
箱体:表示数据的中间50%范围,即上四分位数到下四分位数之间的数据。箱体的长度代表数据的离散度。
中位数:位于箱体中间的线条,表示数据的中间值。
须:由箱体向外延伸的直线,表示数据的最大值和最小值。有时,须的长度可能被限制,以确定是否存在异常值。
异常值:超过须的特定范围的数据点,通常被认为是异常值。在箱线图中,异常值通常用圆点或叉号表示。
箱线图的绘制过程包括计算数据的四分位数和中位数,然后根据这些值绘制箱体和须。箱线图对于检测数据的中心趋势、分散程度以及异常值非常有用,特别适用于比较不同组或类别之间的数据分布。
**累积分布函数:**累计分布函数图是用来表示随机变量的分布情况的图形,显示的是随机变量小于或等于某个特定值的概率,是概率分布函数的积分。通过观察累积分布函数图,可以了解随机变量在不同取值上的累积概率。
关键步骤:
①从Excel文件中读取两个不同蔬菜(小白菜和云南生菜)每月销售信息的数据。
②为每个数据框添加了一个名为"来源"的标签,以便识别不同蔬菜的来源。
③将两个数据框合并为一个名为combined_data的新数据框。
④利用seaborn绘制了一个箱线图,展示了小白菜和云南生菜在2020年7月至2023年2月期间每月销量的分布情况。箱线图显示了销量的中位数、上下四分位数和异常值。
⑤针对小白菜和云南生菜分别提取销量列,计算了它们的累积分布函数,并绘制了两个累积分布函数图。这些图展示了销量在累积概率上的分布情况,帮助了解销量的累积趋势。
关键函数:
①sns.boxplot(x=‘来源’,y=‘销量(千克)’,data=combined_data):使用seaborn绘制箱线图,展示不同蔬菜来源的销量分布情况。
②累积分布函数
np.sort(sales_data):对销量数据进行排序。
np.arange(1,len(sorted_data)+1)/len(sorted_data):计算累积分布函数的概率值。
注:np.arange(1,len(sorted_data)+1)生成一个从 1 到数据集长度的数组,表示每个数据点的累积顺序。然后,除以数据集的长度 len(sorted_data),将排名归一化到范围 [0, 1],从而得到了每个数据点对应的累积概率。
plt.plot(sorted_data,cumulative_prob,marker=‘o’,linestyle=‘-’,color=‘b’):使用matplotlib绘制累积分布函数图。
代码:
1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 import seaborn as sns 5 6 # 读取Excel文件7 file\_path = "某件商品信息.xlsx"8 sheet\_name1 = "小白菜每月销售信息"9 sheet\_name2 = "云南生菜每月销售信息"
10 df1 = pd.read\_excel(file\_path, sheet\_name1)
11 df2 = pd.read\_excel(file\_path, sheet\_name2)
12
13 # 给数据添加标签,以便识别来源
14 df1\['来源'\] = '小白菜'
15 df2\['来源'\] = '云南生菜'
16
17 # 合并两个数据框
18 combined\_data = pd.concat(\[df1, df2\])
19
20 # 设置显示中文
21 plt.rcParams\['font.sans-serif'\] = \['KaiTi'\] # 'SimHei'也可以
22 plt.rcParams\['axes.unicode\_minus'\] = False
23
24 # 绘制箱线图
25 sns.boxplot(x='来源', y='销量(千克)', data=combined\_data)
26 plt.xlabel('')
27 plt.ylabel('销量(千克)')
28 plt.title('小白菜和云南生菜2020年7月至2023年2月月销量箱线图')
29 plt.show()
30
31 # 提取小白菜的销量列
32 sales\_data = df1\['销量(千克)'\]
33
34 # 计算累积分布函数
35 sorted\_data = np.sort(sales\_data)
36 cumulative\_prob = np.arange(1, len(sorted\_data) + 1) / len(sorted\_data)
37
38 # 绘制累积分布函数图
39 plt.plot(sorted\_data, cumulative\_prob, marker='o', linestyle='\-', color='b')
40 plt.xlabel('销量(千克)')
41 plt.ylabel('累积概率')
42 plt.title('小白菜销量累计分布函数图')
43 plt.grid(True)
44 plt.show()
45
46
47 # 提取云南生菜的销量列
48 sales\_data = df2\['销量(千克)'\]
49
50 # 计算累积分布函数
51 sorted\_data = np.sort(sales\_data)
52 cumulative\_prob = np.arange(1, len(sorted\_data) + 1) / len(sorted\_data)
53
54 # 绘制累积分布函数图
55 plt.plot(sorted\_data, cumulative\_prob, marker='o', linestyle='\-', color='b')
56 plt.xlabel('销量(千克)')
57 plt.ylabel('累积概率')
58 plt.title('云南生菜销量累计分布函数图')
59 plt.grid(True)
60 plt.show()
四.附录:数据
单日销售情况.xlsx
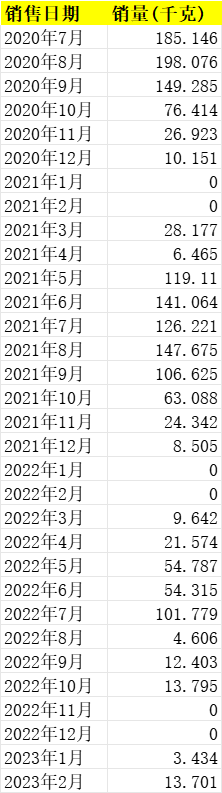
某件商品信息.xlsx 小白菜每月销售信息
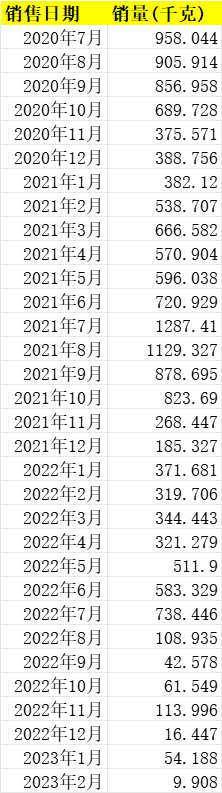
某件商品信息.xlsx 云南生菜每月销售信息
五.后话
如果你也喜欢编程,想通过学习Python获取更高薪资,这里给大家分享一份Python学习资料。
👉Python所有方向的学习路线👈
Python所有方向路线就是把Python常用的技术点做整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照上面的知识点去找对应的学习资源,保证自己学得较为全面。(全套教程文末领取)
👉Python学习视频600合集👈
温馨提示:篇幅有限,已打包文件夹,获取方式在:文末
👉Python70个实战练手案例&源码👈

👉Python副业兼职路线&方法👈
👉 这份完整版的Python全套学习资料已经上传,朋友们如果需要可以直接下方领取
【保证100%免费】