概率论常考知识点汇总

总括

1. 基础概率论

• 概率定义：理解概率是事件发生的可能性度量，范围从0（不可能）到1（必然发生）。
• 概率公理：掌握概率的三大公理，即非负性、规范性和可加性。
• 条件概率：P(A|B)表示在事件B已发生的条件下，事件A发生的概率。
• 贝叶斯定理：用于计算在已知某些证据或数据的条件下，某个假设为真的概率。
• 独立事件与相关事件：理解独立事件的概率乘法规则及相关事件的处理方法。

2. 随机变量及其分布

• 离散随机变量：了解伯努利分布、二项分布、泊松分布等，以及它们的应用场景。
• 连续随机变量：熟悉均匀分布、正态分布（高斯分布）、指数分布等，掌握其概率密度函数(PDF)和累积分布函数(CDF)。
• 联合分布与边缘分布：理解多维随机变量的联合分布，及其边缘分布的计算方法。
• 条件分布与协方差：学习如何基于给定条件下一个随机变量的分布，以及随机变量间的相互依赖关系。

3. 数理统计基础

• 点估计：了解均值、中位数、众数作为参数的估计方法，以及最大似然估计和最小二乘法。
• 区间估计：掌握置信区间的概念，理解如何构建参数的置信区间，特别是正态分布情况下的Z检验和t检验。
• 假设检验：熟悉原假设与备择假设，掌握单样本和双样本检验，包括显著性水平、p值的理解与应用。
• 方差分析(ANOVA)：理解方差分析的基本原理，用于比较两个以上样本均值是否存在显著差异。

4. 高级主题（根据兴趣选择）

• 贝叶斯统计：深入理解贝叶斯分析，包括先验概率、后验概率和贝叶斯推断。
• 大数定律与中心极限定理：掌握这两个定理对于统计推断的重要意义。
• 非参数统计：了解当数据不符合正态分布或其他特定分布时，使用如卡方检验、秩和检验等非参数方法。
• 时间序列分析：研究随时间变化的数据序列，涉及自回归模型(AR)、移动平均模型(MA)及它们的组合ARIMA等。

基本概率公式

在概率论中，事件之间的关系及其运算主要涉及交集、并集、补事件以及条件概率，这些是理解和计算复合事件概率的基础。下面详细解释这些概念：

1. 交集 (Intersection)

• 定义：如果A和B是两个事件，那么A∩B表示事件A和事件B同时发生的事件。即A和B的交集包含了所有既属于A又属于B的样本点。
• 概率运算：事件A和B同时发生的概率，记作P(A∩B)，等于各自发生的概率的乘积，仅当A和B是独立事件时，即P(A∩B) = P(A) * P(B)。若A和B不独立，则需要根据具体情况计算。

2. 并集 (Union)

• 定义：事件A和B的并集，记作A∪B，包含所有至少属于A或B（或两者都属于）的样本点。

• 概率运算

  ：事件A或B至少有一个发生的概率，记作P(A∪B)，可以通过以下公式计算：

  𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)P(A∪B)=P(A)+P(B)−P(A∩B)

  这里减去P(A∩B)是为了避免A和B共同部分被重复计算。

3. 补事件 (Complement)

• 定义：对于任意事件A，它的补事件记作A’或𝐴ˉAˉ，表示A不发生的事件。
• 概率运算：一个事件与其补事件的概率之和等于1，即P(A’) = 1 - P(A)。补事件的概念简化了某些问题的处理，特别是在计算“至少”或“至多”这类问题时。

4. 条件概率 (Conditional Probability)

• 定义：在事件B已经发生的条件下，事件A发生的概率，记作P(A|B)。

• 计算公式

  ：

  𝑃(𝐴∣𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐵)P(A∣B)=P(B)P(A∩B)

  只有当P(B) > 0时，上述公式才有意义。

5. 乘法法则 (Multiplication Rule)

• 用于计算两个事件同时发生的概率，特别地，它也关联条件概率和无条件概率的关系：

  𝑃(𝐴∩𝐵)=𝑃(𝐴)⋅𝑃(𝐵∣𝐴)=𝑃(𝐵)⋅𝑃(𝐴∣𝐵)P(A∩B)=P(A)⋅P(B∣A)=P(B)⋅P(A∣B)

  这表明可以从不同的角度理解两个事件同时发生的概率

随机变量

随机变量

定义：随机变量是将随机试验的结果与实数建立对应关系的函数。它可以分为两种类型：

• 离散随机变量：取值为有限个或可数无限个确定值的随机变量，如抛掷一枚骰子得到的点数。
• 连续随机变量：取值可以在某个区间内取任何值（理论上无限多）的随机变量，如测量一个人的身高。

分布函数

定义：随机变量 𝑋X 的分布函数（Cumulative Distribution Function, CDF），记作 𝐹(𝑥)F(x)，定义为随机变量 𝑋X 取值小于或等于 𝑥x 的概率。形式上，对于任意实数 𝑥x，有：

𝐹(𝑥)=𝑃(𝑋≤𝑥)F(x)=P(X≤x)

性质：

1. 单调性：分布函数 𝐹(𝑥)F(x) 是单调不减的，即如果 𝑥1<𝑥2x1<x2，则 𝐹(𝑥1)≤𝐹(𝑥2)F(x1)≤F(x2)。
2. 右连续性：𝐹(𝑥)F(x) 在每一个点 𝑥x 处都是右连续的，意味着 𝐹(𝑥)F(x) 在 𝑥x 的右侧极限存在，并等于 𝐹(𝑥)F(x) 在 𝑥x 处的值。
3. 边界条件：分布函数在 −∞−∞ 处为 0，在 +∞+∞ 处为 1，即 𝐹(−∞)=0F(−∞)=0，𝐹(+∞)=1F(+∞)=1。
4. 概率计算：对于任意两个实数 𝑎a 和 𝑏b，若 𝑎<𝑏a<b，则随机变量 𝑋X 落在区间 (𝑎,𝑏](a,b] 内的概率为 𝑃(𝑎<𝑋≤𝑏)=𝐹(𝑏)−𝐹(𝑎)P(a<X≤b)=F(b)−F(a)。

分布函数的分类

• 离散随机变量的分布函数：通常是阶梯函数，每一步的跳跃高度代表相应值的概率质量。
• 连续随机变量的分布函数：对于连续型随机变量，分布函数是连续的，而概率密度函数 𝑓(𝑥)f(x) 与分布函数的关系为 𝐹′(𝑥)=𝑓(𝑥)F′(x)=f(x) 在 𝑓(𝑥)f(x) 连续的地方成立，即分布函数的导数（在定义的地方）给出了概率密度。

离散型概率以及分布

离散型概率分布描述的是离散随机变量取不同值的概率。离散随机变量只能取有限个或可数无限个值，每个值都有一个明确的概率与之对应。下面是几个典型的离散型概率分布及其特征：

1. 伯努利分布 (Bernoulli Distribution)

• 定义：伯努利试验是指只有两种可能结果的试验，通常称为“成功”和“失败”，且每次试验这两种结果的概率保持不变。设成功的概率为 𝑝p，失败的概率为 1−𝑝1−p，则一个伯努利随机变量 𝑋X 取值为1（成功）的概率为 𝑝p，取值为0（失败）的概率为 1−𝑝1−p。
• 概率质量函数 (PMF)：𝑃(𝑋=𝑘)=𝑝𝑘(1−𝑝)1−𝑘P(X=k)=pk(1−p)1−k，其中 𝑘=0,1k=0,1。

2. 二项分布 (Binomial Distribution)

• 定义：在一系列独立的伯努利试验中，成功次数的分布称为二项分布。如果进行了 𝑛n 次独立的伯努利试验，每次试验成功的概率为 𝑝p，则在这些试验中恰好成功 𝑘k 次的概率服从二项分布。
• PMF：𝑃(𝑋=𝑘)=(𝑛𝑘)𝑝𝑘(1−𝑝)𝑛−𝑘P(X=k)=(kn)pk(1−p)n−k，其中 (𝑛𝑘)(kn) 是组合数，表示从 𝑛n 个不同元素中取出 𝑘k 个元素的组合方式数量。

3. 泊松分布 (Poisson Distribution)

• 定义：泊松分布常用来描述在一定时间或空间区域内，稀有事件发生次数的概率分布。如果平均每单位时间（或空间）内事件发生的次数为 𝜆λ，则在任意时间（或空间）区间内事件发生 𝑘k 次的概率遵循泊松分布。
• PMF：𝑃(𝑋=𝑘)=𝜆𝑘𝑒−𝜆𝑘!P(X=k)=k!λke−λ，其中 𝜆λ 是平均事件数，𝑒e 是自然对数的底。

4. 几何分布 (Geometric Distribution)

• 定义：几何分布描述的是首次成功前进行试验的次数。在一个伯努利试验序列中，直到首次成功所需试验的次数 𝑋X 服从几何分布，每次试验成功的概率为 𝑝p。
• PMF：𝑃(𝑋=𝑘)=(1−𝑝)𝑘−1𝑝P(X=k)=(1−p)k−1p，𝑘=1,2,3,…k=1,2,3,…。

5. 负二项分布 (Negative Binomial Distribution)

• 定义：负二项分布描述的是在第 𝑟r 次成功之前已经发生了 𝑘k 次失败的概率分布。它扩展了几何分布，考虑了达到固定成功次数前的失败次数。
• PMF：𝑃(𝑋=𝑘)=(𝑘+𝑟−1𝑘)𝑝𝑟(1−𝑝)𝑘P(X=k)=(kk+r−1)pr(1−p)k，其中 𝑟r 是预先设定的成功次数。

组合公式

组合公式是用来计算从n个不同元素中不重复地选择r个元素的方法数，记作 𝐶(𝑛,𝑟)C(n,r) 或者 “𝑛n 选 𝑟r”，也称为二项式系数。公式如下：

𝐶(𝑛,𝑟)=𝑛!𝑟!(𝑛−𝑟)!C(n,r)=r!(n−r)!n!

其中，

• 𝑛!n! 表示n的阶乘，即 𝑛×(𝑛−1)×(𝑛−2)×⋯×1n×(n−1)×(n−2)×⋯×1，
• 𝑟!r! 是r的阶乘，
• 𝑛−𝑟n−r 代表剩余未被选择的元素数量，
• "!"符号表示阶乘运算。

当 𝑛<𝑟n<r 时，𝐶(𝑛,𝑟)C(n,r) 定义为0，因为无法从较少的元素中选择更多的元素。

这个公式在概率论、统计学、组合数学以及日常生活中解决排列组合问题时非常有用。

连续型随机变量

连续性随机变量是概率论中的一种重要概念，它用来描述那些可能取值无法逐一列举，而是在某个区间内可以取任意实数值的随机变量。与离散型随机变量不同，连续型随机变量在数轴上的取值是连续的，其概率分布需要用概率密度函数（probability density function, PDF）来描述，而不是概率质量函数。以下是连续性随机变量的详细解析：

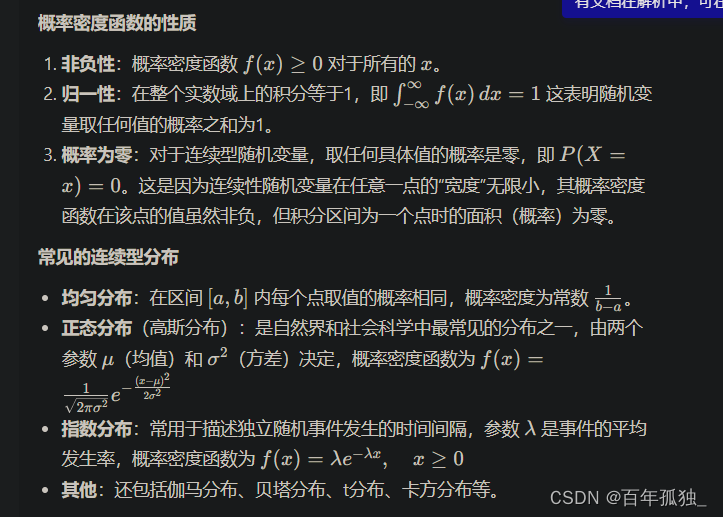
常见的连续型随机变量的及其分布

离散型随机变量函数的分布

离散型随机变量函数的分布是指如果有一个离散型随机变量 𝑋X，其概率质量函数（probability mass function, PMF）为 𝑃(𝑋=𝑥𝑖)=𝑝𝑖P(X=xi)=pi，对于 𝑋X 的某个函数 𝑌=𝑔(𝑋)Y=g(X)，我们想要找到 𝑌Y 的分布，即求解 𝑌Y 的概率质量函数 𝑃(𝑌=𝑦𝑗)P(Y=yj)。

处理离散型随机变量函数分布的一般步骤如下：

1. 确定 𝑌Y 的可能值：首先需要明确通过函数 𝑔g 转换后，𝑌Y 可能取到的所有值。这通常需要考虑 𝑋X 的所有可能取值，并应用 𝑔g 函数。
2. 计算每个 𝑦𝑗yj 的概率：对于 𝑌Y 的每一个可能值 𝑦𝑗yj，需要找出所有能使 𝑔(𝑋)=𝑦𝑗g(X)=yj 的 𝑋X 的值集合 𝑆𝑗Sj，然后将这些 𝑋X 值对应的概率相加来得到 𝑃(𝑌=𝑦𝑗)P(Y=yj)。

𝑃(𝑌=𝑦𝑗)=∑𝑥𝑖∈𝑆𝑗𝑃(𝑋=𝑥𝑖)P(Y=yj)=∑xi∈SjP(X=xi)

这里，𝑆𝑗Sj 是使得 𝑔(𝑥𝑖)=𝑦𝑗g(xi)=yj 成立的所有 𝑥𝑖xi 的集合。

1. 特殊情况处理：如果函数 𝑔g 导致某些 𝑌Y 的值没有对应的 𝑋X 值（即 𝑔g 不是满射），则那些 𝑌Y 的值的概率为0。反之，如果 𝑔g 将多个 𝑋X 映射到同一个 𝑌Y 值，则需要累加这些 𝑋X 值的概率。

举例说明：

假设 𝑋X 是一个离散型随机变量，取值为 {1, 2, 3}，相应的概率分别为 1331。考虑函数 𝑌=𝑔(𝑋)=𝑋2Y=g(X)=X2。

• 确定 𝑌Y 的可能值：应用 𝑔g 后，𝑌Y 的可能值为 {1, 4, 9}。
• 计算每个 𝑦𝑗yj 的概率：
  • 对于 𝑌=1Y=1，只有当 𝑋=1X=1 时成立，因此 𝑃(𝑌=1)=𝑃(𝑋=1)=13P(Y=1)=P(X=1)=31。
  • 对于 𝑌=4Y=4，只有当 𝑋=2X=2 时成立，所以 𝑃(𝑌=4)=𝑃(𝑋=2)=13P(Y=4)=P(X=2)=31。
  • 对于 𝑌=9Y=9，只有当 𝑋=3X=3 时成立，故 𝑃(𝑌=9)=𝑃(𝑋=3)=13P(Y=9)=P(X=3)=31。

最终，我们得到了 𝑌Y 的概率质量函数 𝑃(𝑌=1)=13P(Y=1)=31, 𝑃(𝑌=4)=13P(Y=4)=31, 𝑃(𝑌=9)=13P(Y=9)=31，这表明 𝑌Y 也是一个均匀分布的离散型随机变量。

二维连续型随机变量及其分布

二维连续性随机变量指的是由两个连续随机变量构成的随机向量，它们可以同时描述两个相互关联的连续随机现象。二维连续性随机变量的联合分布由联合概率密度函数（Joint Probability Density Function, JPDF）来描述，而边缘分布则描述了每个变量单独的分布情况。以下是二维连续性随机变量及其分布的详细说明：

协方差

计算协方差

计算协方差的具体步骤可以通过一个简单的例子来说明。假设我们有一组关于两个变量 𝑋X 和 𝑌Y 的数据对，分别是：

𝑋X	𝑌Y
2	4
4	6
6	8
8	10

首先，我们计算每个变量的平均值（均值）：

𝐸[𝑋]=2+4+6+84=204=5E[X]=42+4+6+8=420=5𝐸[𝑌]=4+6+8+104=284=7E[Y]=44+6+8+10=428=7

接下来，我们使用样本协方差的公式来计算协方差：

𝐶𝑜𝑣^(𝑋,𝑌)=1𝑛−1∑𝑖=1𝑛(𝑥𝑖−𝑥‾)(𝑦𝑖−𝑦‾)Cov(X,Y)=n−11∑i=1n(xi−x)(yi−y)

其中 𝑛=4n=4 是样本量，𝑥‾=5x=5 是 𝑋X 的均值，𝑦‾=7y=7 是 𝑌Y 的均值。现在，我们计算每一项并求和：

• 对于第一对数据（2, 4）：(2−5)(4−7)=(−3)(−3)=9(2−5)(4−7)=(−3)(−3)=9
• 对于第二对数据（4, 6）：(4−5)(6−7)=(−1)(−1)=1(4−5)(6−7)=(−1)(−1)=1
• 对于第三对数据（6, 8）：(6−5)(8−7)=(1)(1)=1(6−5)(8−7)=(1)(1)=1
• 对于第四对数据（8, 10）：(8−5)(10−7)=(3)(3)=9(8−5)(10−7)=(3)(3)=9

现在，将这些乘积相加并应用公式：

𝐶𝑜𝑣^(𝑋,𝑌)=14−1×(9+1+1+9)=13×20=203Cov(X,Y)=4−11×(9+1+1+9)=31×20=320

因此，变量 𝑋X 和 𝑌Y 之间的样本协方差大约为 6.676.67。这个正值表明 𝑋X 和 𝑌Y 之间存在正相关关系，即随着 𝑋X 的增加，𝑌Y 也倾向于增加。