Powered by:NEFU AB-IN
Link
文章目录
- 1027. 方格取数
- 题意
- 思路
- 代码
1027. 方格取数
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
典型的数字三角形模型的dp,但是不是走一遍,而是走两遍。此时不能贪心的做,做一遍dp,再做一遍dp
题目应该等价于,两个人同时走
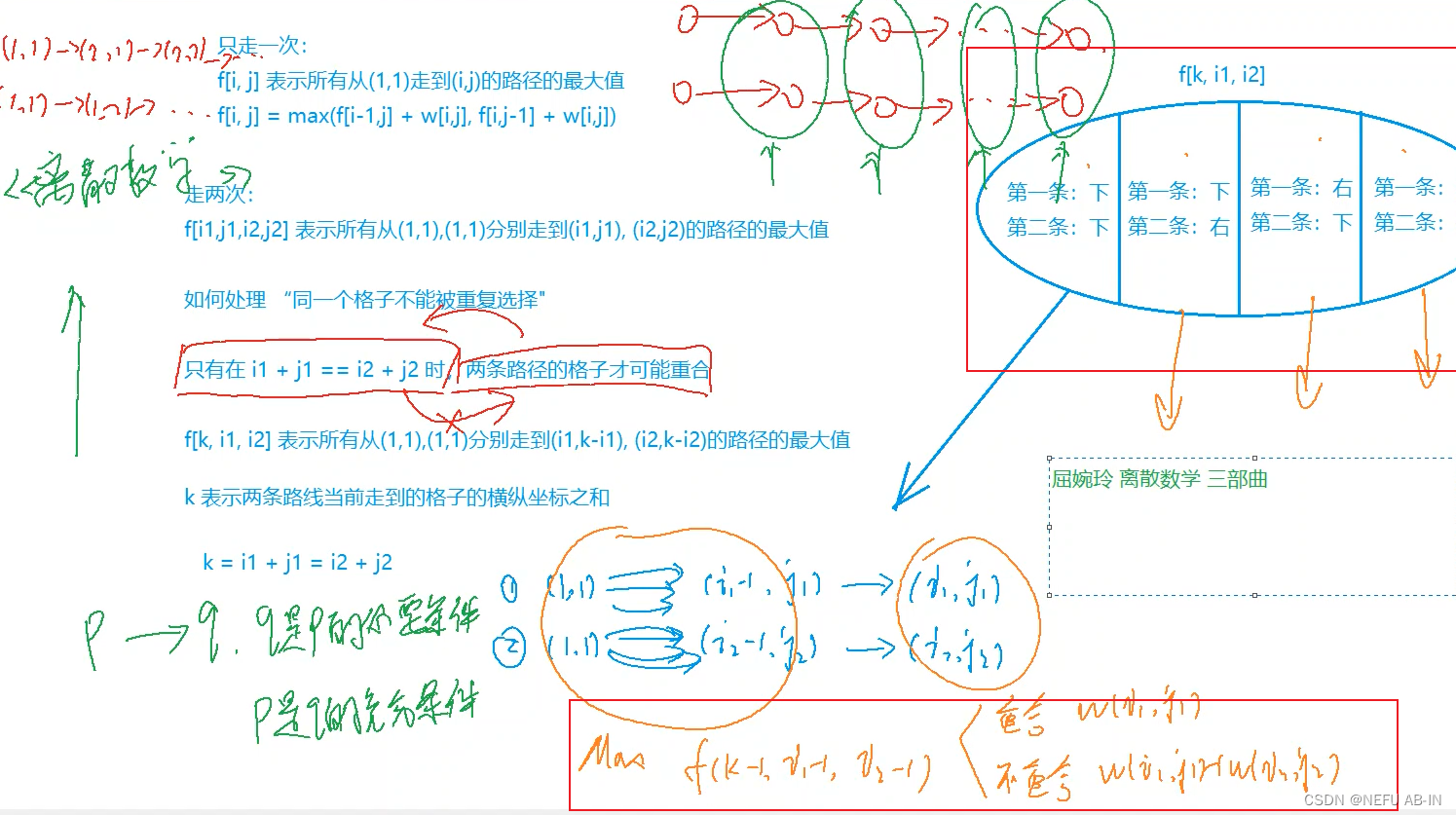
思路为再加一维的dp,记录两人的总步数,这样三维dp,就会分为四种情况,而不是之前的两个情况(由上和左走过来)
具体思路如下图
# import
from sys import setrecursionlimit, stdin, stdout, exit
from collections import Counter, deque, defaultdict
from heapq import heapify, heappop, heappush, nlargest, nsmallest
from bisect import bisect_left, bisect_right
from datetime import datetime, timedelta
from string import ascii_lowercase, ascii_uppercase
from math import log, gcd, sqrt, fabs, ceil, floor
from types import GeneratorType
from typing import TypeVar, List, Dict, Any, Callable# Data structure
class SA:def __init__(self, x, y):self.x = xself.y = ydef __lt__(self, other):return self.x < other.x# Constants
N = int(20) # If using AR, modify accordingly
M = int(20)
INF = int(2e9)# Set recursion limit
setrecursionlimit(INF)# Read
input = lambda: stdin.readline().rstrip("\r\n") # Remove when Mutiple data
read = lambda: map(int, input().split())
read_list = lambda: list(map(int, input().split()))# Func
class std:# Recursion@staticmethoddef bootstrap(f, stack=None):if stack is None:stack = []def wrappedfunc(*args, **kwargs):if stack:return f(*args, **kwargs)else:to = f(*args, **kwargs)while True:if isinstance(to, GeneratorType):stack.append(to)to = next(to)else:stack.pop()if not stack:breakto = stack[-1].send(to)return toreturn wrappedfuncletter_to_num = staticmethod(lambda x: ord(x.upper()) - 65) # A -> 0num_to_letter = staticmethod(lambda x: ascii_uppercase[x]) # 0 -> Aarray = staticmethod(lambda x=0, size=N: [x] * size)array2d = staticmethod(lambda x=0, rows=N, cols=M: [std.array(x, cols) for _ in range(rows)])max = staticmethod(lambda a, b: a if a > b else b)min = staticmethod(lambda a, b: a if a < b else b)filter = staticmethod(lambda func, iterable: list(filter(func, iterable)))# —————————————————————Division line ——————————————————————n, = read()
w = std.array2d(0, N, N)
f = [std.array2d(0, N, N) for _ in range(N * 2)]while True:x, y, num = read()if x + y + num == 0:breakw[x][y] = numfor k in range(2, n + n + 1):for i1 in range(1, n + 1):for i2 in range(1, n + 1):j1 = k - i1j2 = k - i2if 1 <= j1 <= n and 1 <= j2 <= n:t = w[i1][j1]if i1 != i2:t += w[i2][j2]f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2 - 1] + t,f[k - 1][i1 - 1][i2] + t,f[k - 1][i1][i2 - 1] + t,f[k - 1][i1][i2] + t)print(f[n + n][n][n])