一、冒泡排序

冒泡排序（Bubble Sort），顾名思义，就是指越小的元素会经由交换慢慢“浮”到数列的顶端。

算法原理

1. 从左到右，依次比较相邻的元素大小，更大的元素交换到右边；
2. 从第一组相邻元素比较到最后一组相邻元素，这一步结束最后一个元素必然是参与比较的元素中最大的元素；
3. 按照大的居右原则，重新从左到后比较，前一轮中得到的最后一个元素不参4与比较，得出新一轮的最大元素；
4. 按照上述规则，每一轮结束会减少一个元素参与比较，直到没有任何一组元素需要比较。

代码实现

// 冒泡排序
void BubbleSort(int* arr, int n)
{int i = 0;for (i = 0; i < n - 1; ++i) // 冒泡排序趟数{int j = 0;int flag = 1;for (j = 0; j < n - i - 1; ++j) // 待排序区间进行比较交换{if (arr[j] > arr[j + 1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;flag = 0;}}if (flag == 1){// 说明已经有序break;}}
}

 拓展：

 O()

二、快速排序

快速排序（Quick Sort），是冒泡排序的改进版，之所以“快速”，是因为使用了分治法。它也属于交换排序，通过元素之间的位置交换来达到排序的目的。

算法原理

在序列中随机挑选一个元素作基准，将小于基准的元素放在基准之前，大于基准的元素放在基准之后，再分别对小数区与大数区进行排序。

一趟快速排序的具体做法是：

1. 设两个指针 i 和 j，分别指向序列的头部和尾部；
2. 先从 j 所指的位置向前搜索，找到第一个比基准小的值，把它与基准交换位置；
3. 再从 i 所指的位置向后搜索，找到第一个比基准大的值，把它与基准交换位置；
4. 重复 2、3 两步，直到 i = j。

仔细研究一下上述算法我们会发现，在排序过程中，对基准的移动其实是多余的，因为只有一趟排序结束时，也就是 i = j 的位置才是基准的最终位置。

由此可以优化一下算法：

1. 设两个指针 i 和 j，分别指向序列的头部和尾部；
2. 先从 j 所指的位置向前搜索，找到第一个比基准小的数值后停下来，再从 i 所指的位置向后搜索，找到第一个比基准大的数值后停下来，把 i 和 j 指向的两个值交换位置；
3. 重复步骤 2，直到 i = j，最后将相遇点指向的值与基准交换位置。

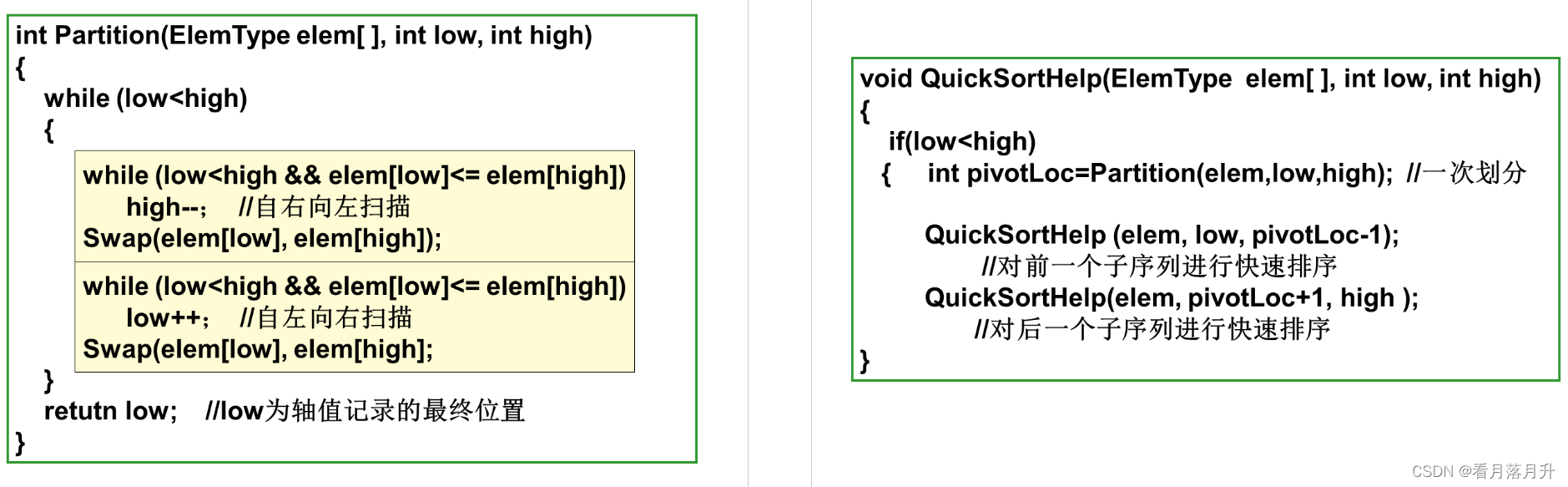
代码：

void QuickSort(int array[], int low, int high) {int i = low; int j = high;if(i >= j) {return;}int temp = array[low];while(i != j) {while(array[j] >= temp && i < j) {j--;}while(array[i] <= temp && i < j) {i++;}if(i < j) {swap(array[i], array[j]);}}//将基准temp放于自己的位置，（第i个位置）swap(array[low], array[i]);QuickSort(array, low, i - 1);QuickSort(array, i + 1, high);
}

三、插入排序

直接插入排序（Straight Insertion Sort），是一种简单直观的排序算法，它的基本操作是不断地将尚未排好序的数插入到已经排好序的部分，好比打扑克牌时一张张抓牌的动作。在冒泡排序中，经过每一轮的排序处理后，序列后端的数是排好序的；而对于插入排序来说，经过每一轮的排序处理后，序列前端的数都是排好序的。

算法原理

先将第一个元素视为一个有序子序列，然后从第二个元素起逐个进行插入，直至整个序列变成元素非递减有序序列为止。如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入大相等元素的后面。整个排序过程进行 n-1 趟插入

代码：

//========================写法1=======================
void insert_sort(int *arr, int len){int i, j;for (i = 1; i < len; i++){int tmp = arr[i];//待插入数for (j = i; j > 0 && arr[j - 1] > tmp; j--){arr[j] = arr[j - 1];//大的数依次右移}arr[j] = tmp;}
}//==========================写法2======================
void insert_sort_1(int *arr, int n)
{int i = 0, j = 0;for (i = 1; i < n; i++){j = i;//一直拿当前数与前面数比，有<=它的就停止，没有接着交换位置并往前比while (j >= 1){if (arr[j] < arr[j - 1])	{swap(arr, j, j - 1);}j--;}}
}

四、希尔排序

希尔排序（Shell’s Sort）是第一个突破 O(n²) 的排序算法，是直接插入排序的改进版，又称“缩小增量排序”（Diminishing Increment Sort）。它与直接插入排序不同之处在于，它会优先比较距离较远的元素。

算法原理

先将整个待排序列分割成若干个子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

子序列的构成不是简单地“逐段分割”，将相隔某个增量的记录组成一个子序列，让增量逐趟缩短，直到增量为 1 为止。

 

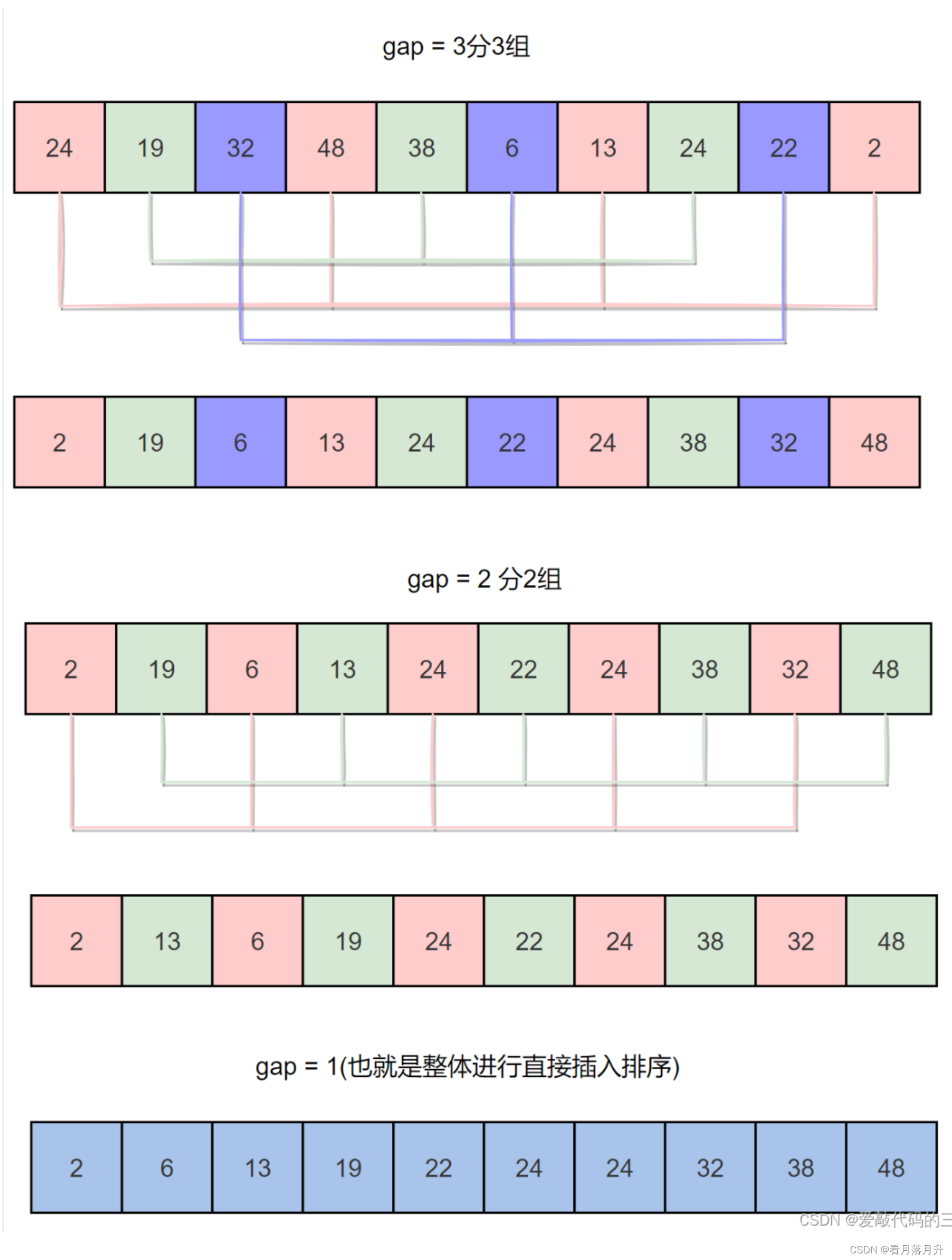
代码实现

这里的代码是通过一次就把所有元素排序完成。

• gap的取值保证最后为1就可以了
• gap不等于1之前其实都是预排序，让数据趋近于有序。

// 希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//保证最后gap为1就可以了int i = 0;for (i = 0; i < n - gap; ++i)//多组元素同时进行插入排序{int end = i;int tmp = arr[end+gap];while (end >= 0){if (arr[end] > tmp){arr[end+gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}

五、选择排序

每次从待排序的数据元素中选出最小(或最大)的一个元素，存放在序列的起始位置，直到全部待排序的元素排序完。

原理
每次从无序区间中选取一个最大(或最小)的一个元素，存放在无序区间的最后(或最前)，直到全部待排序的元素排序完。

在元素集合中a r r [ i ]   a r r [ n − 1 ] arr[i]~arr[n-1]arr[i] arr[n−1]中选择最大(最小的元素)
若它不是这组元素中的最后一个(第一个元素)，则将它与这组元素中的最后一个(第一个)元素交换
在剩余的a r r [ i ]   a r r [ n − 2 ] arr[i]~arr[n-2]arr[i] arr[n−2]集合中，重复此步骤，直到集合中剩余一个元素为止

 

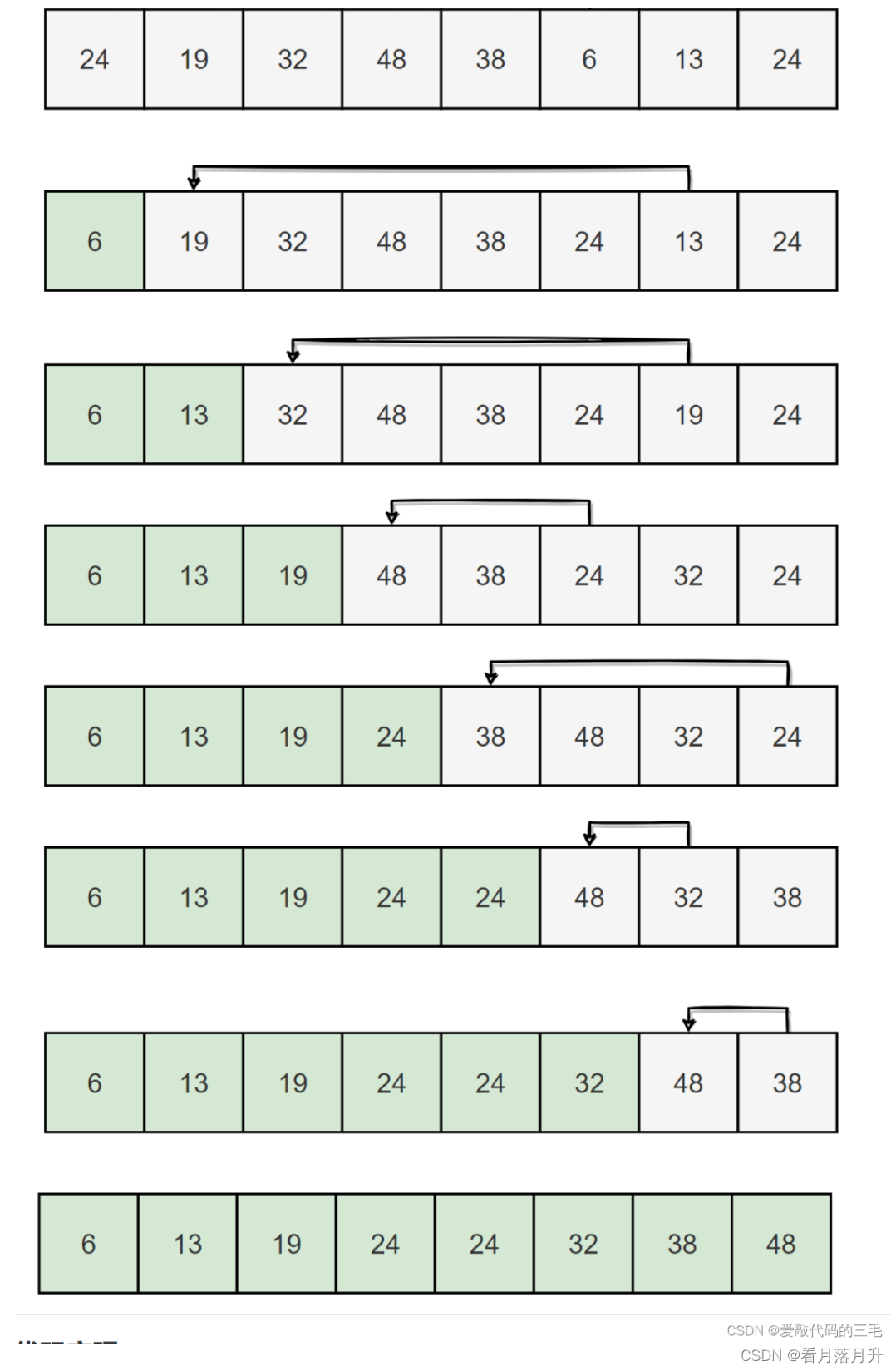
代码：

// 选择排序
void SelectSort(int* arr, int n)
{int i = 0;for (i = 0; i < n - 1; ++i){int minIndex = i;//记录待排序区间最小元素下标int j = 0;for (j = i + 1; j < n; ++j){if (arr[minIndex] > arr[j]){minIndex = j;}}int tmp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = tmp;}
}

六、堆排序

堆排序是利用数据结构堆的特性来进行排序，它也是一种选择排序，它通过堆来选取数据。排升序建大堆，排降序建小堆。
堆的详细介绍可以看这一篇文章数据结构堆的详解

原理
每次将堆顶元素和最后一个元素进行交换，再进行向下调整，然后缩小待排序区间，直到数据有序，因为堆顶的元素一定是一组数据中的最大或者最小值。

注意：向下调整的前提是，这个根节点的左右子树一定要是一个堆(大堆或小堆)

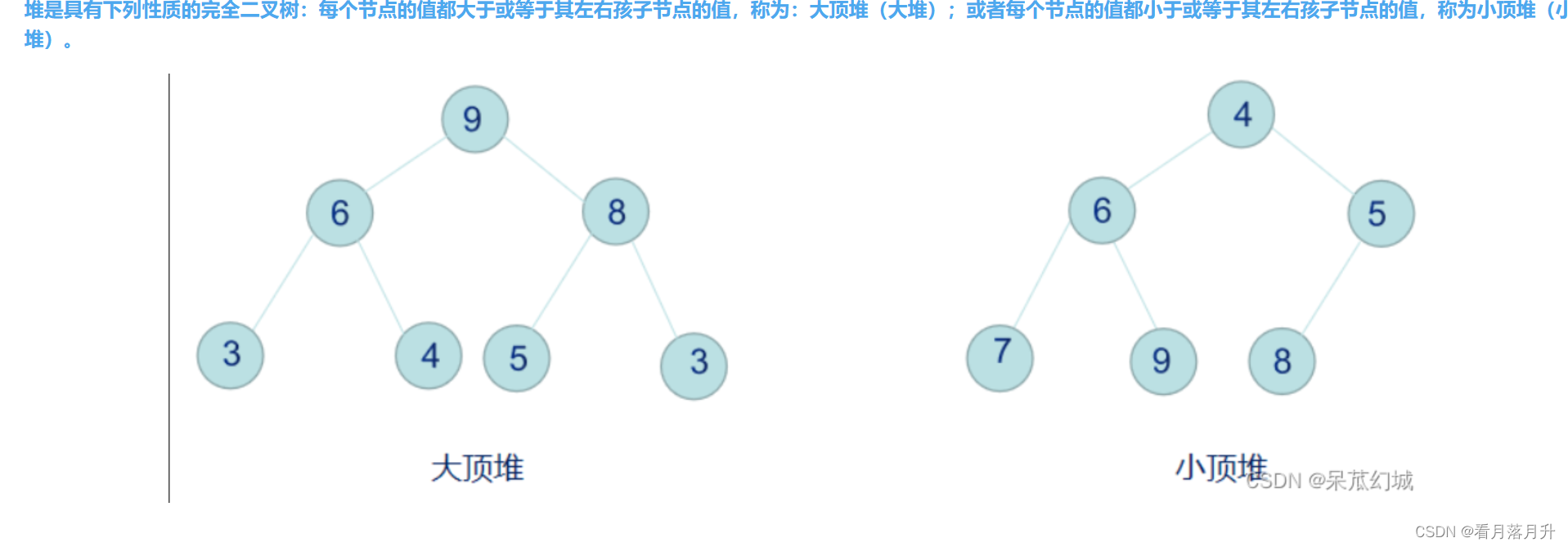
代码

void HeapAdjust(int* arr, int start, int end)
{int tmp = arr[start];for (int i = 2 * start + 1; i <= end; i = i * 2 + 1){if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子{i++;}//i一定是左右孩子的最大值if (arr[i] > tmp){arr[start] = arr[i];start = i;}else{break;}}arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{//第一次建立大根堆，从后往前依次调整for(int i=(len-1-1)/2;i>=0;i--){HeapAdjust(arr, i, len - 1);}//每次将根和待排序的最后一次交换，然后在调整int tmp;for (int i = 0; i < len - 1; i++){tmp = arr[0];arr[0] = arr[len - 1-i];arr[len - 1 - i] = tmp;HeapAdjust(arr, 0, len - 1-i- 1);}
}
int main()
{int arr[] = { 9,5,6,3,5,3,1,0,96,66 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));printf("排序后为:");for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}