电源简析和全桥LLC模型分析
1.1模拟电源、开关电源和数字电源简介
1.1.1 模拟电源
模拟电源:即变压器电源,通过铁芯、线圈来实现,线圈的匝数决定了两端的电压比,铁芯的作用是传递变化磁场,(我国)主线圈在 50HZ 频率下产生了变化的磁场,这个变化的磁场通过铁芯传递到副线圈,在副线圈里就产生了感应电压,于是变压器就实现了电压的转变。
模拟电源的缺点:线圈、铁芯本身是导体,那么它们在转化电压的过程中会 由于自感电流而发热(损耗),所以变压器的效率很低,一般不会超过 35%。
大功率设备需要变压器提供更多的功率输出,那么只有通过线圈匝数的增加、铁芯体积的增大来实现,匝数和铁芯体积的增加就会加重其损耗,所以,大功率变压器必须做的非常大,这样就会导致:模拟电源笨重,发热量大。
1.1.2 开关电源
开关电源:在电流进入变压器之前,通过晶体管的开关功能,将我们通常50HZ 的电流频率提升到数百至数万HZ,在这么高的频率下,磁场变化频率也达到数百至数万HZ,那么就可以减少线圈匝数、铁芯体积,获得同样的电压转化比。由于线圈匝数、铁芯体积的减少,损耗大大降低,一般开关电源效率达到90%,而体积可以做的非常小,重量也大幅减轻,并且输出稳定,所以开关电源具有模拟电源难以达到的优点。(开关电源也有自己的不足,如输出电压有纹波及开关噪声,模拟线性电源是没有的)。
1.1.3 数字电源
在简单易用、参数变更要求不多的应用场合,模拟电源产品更具优势,因为其应用的针对性可以通过硬件固化来实现,而在可控因素较多、实时反应速度更快、需要多个模拟系统电源管理的、复杂的高性能系统应用中,数字电源则更有优势。此外,在复杂的多系统业务中,相对模拟电源,数字电源是通过软件编程来实现多方面的应用,其具备的可扩展性与重复使用性使用户可以方便更改工作参数,优化电源系统。通过实时过电流保护与管理,它还可以减少外围器件的数量。
数字电源有用DSP控制的,还有用MCU控制的。相对来讲,DSP控制的电源 采用数字滤波方式,较MCU控制的电源更能满足复杂的电源需求、实时反应速度更快、电源稳压性能更好。
1.2 AC/DC、DC/AC和DC/DC简介
1.2.1 AC/DC
AC/DC电源也称一类电源,是交流转换成直流,它一般从电网获取能量,经过高压整流滤波得到一个直流高压,供DC/DC变换器使用,通过DC/DC变换器输出一个或几个稳定的直流电压,功率从几瓦到几千瓦,适用于不同的应用场合。
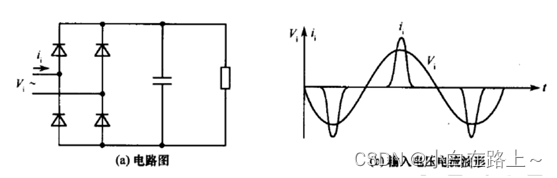
传统应用中输入侧交流电源经全波整流后,一般接一个大电容器,以得到波
形较为平直的直流电压。整流器-滤波电路是一种非线性元件和储能元件的组合,
因此,虽然输入交流电压是正弦的,但输入交流电流却严重畸变,呈现脉冲状。
由此可见,大量应用整流电路,会在电网端引起畸变的非正弦电流,造成严重的后果就是,谐波电流对电网有很高危害作用,同时,设备的输入端功率因数会大大下降。同时对于AC/DC场合,DC输出端通常要求具备稳定的直流母线电
压,甚至要求可调节。因此需要引入PFC调整,PFC有3个重要作用:
A) 改善输入电流谐波
B) 改善输入PF值
C) 稳定输出电压
1.2.2 DC/AC
DC/AC电源也称逆变电源,它是由一次电源或直流电池组提供一个直流输入电压,经过DC/AC变换器输出频率可变的交流电压。
逆变电源用途很广,常用的领域有光伏逆变、变频调速、新能源车PMSM电机驱动等。
重要参数指标:
A) 输出频率可调
B) 输出幅值可调
C) 输出稳定的正弦或方波
1.2.3 DC/DC
DC/DC电源也称二次电源,它是由一次电源或直流电池组提供一个直流输入电压,经过DC/DC变换器输出一个或几个稳定的直流电压。
DC/DC开关电源常见的拓扑有:Buck降压、Boost升压、Buck-Boost升降压、
反激、正激、推挽、半桥和全桥等8种。
全桥LLC的控制方法有PFM(变频控制)、移相全桥和有限双极性PWM(变宽控制),在后面控制软件的章节中,将重点阐述全桥LLC的有限双极性的发波控制原理。
重要参数指标:
A) 输出电压稳定(相位裕度)
B) 输出电压动态响应好 (增益裕度、带宽)
C) 抗高频干扰能力强(穿越频率、带宽)
总结一句话就是:即快又稳还抗干扰。
1.3 全桥LLC谐振变换器模型分析
1.3.1 概述
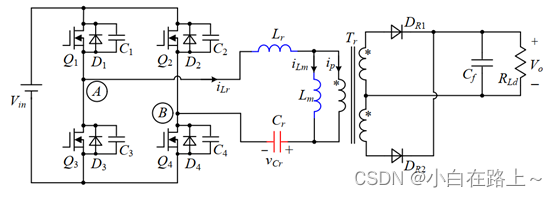
图 1.1 主电路结构图
全桥LLC谐振变换器的结构如图3.1所示。图中,Q1~Q4为主功率开关管, D1D4、C1C4分别为它们的体二极管及其漏源极之间的寄生电容。Tr为主功率变压器。DR1和 DR2为输出整流二极管,Cf为输出滤波电容,RLd为负载电阻。 谐振电感 Lr(包括变压器的原边漏感)、励磁电感 Lm和谐振电容 Cr组成 LLC谐振变换器的谐振网络。其中,励磁电感 Lm集成在变压器里;谐振电容 Cr串联在原边回路中,同时起到隔直电容的作用。
为了方便讨论,定义谐振电感 Lr和谐振电容 Cr的谐振频率为串联谐振频率,记作 fr;当谐振电流iLr下降到和励磁电感电流iLm相等时,励磁电感 Lm、谐振电感 Lr与谐振电容Cr一起谐振,此时的谐振频率定义为串并联谐振频率,记作 fm。两个谐振频率的表达式如下:

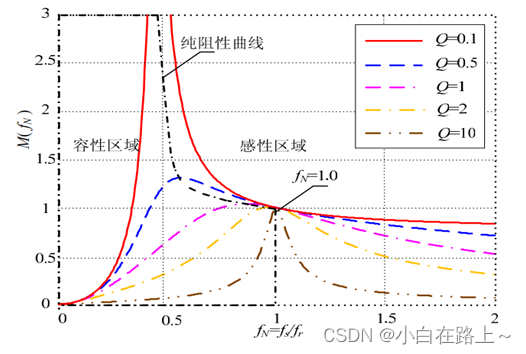
图 1. 2 LLC 谐振变换器增益曲线
图1.2给出了LLC谐振变换器在不同品质因数Q下的输入输出增益曲线。由图1.2可知:当开关频率fs<fm时,变换器工作在容性区域,此情况下,励磁电流将会在开关管关断前反向,开关管将不能实现ZVS开通;当开关频率fs>fm时,变换器工作在感性区域,原边开关管能够实现ZVS开通;若将变换器的开关频率进一步限制在fm<fs<fr时,副边整流二极管可以实现ZCS关断。
综上分析,LLC 谐振变换器主要有以下优点:
1)可以在较宽负载范围内实现原边开关管的ZVS开通;
2)可以在较宽负载范围内实现副边整流二极管的ZCS关断,避免反向恢复带来的损耗及电压尖峰;
3)可利用变压器的漏感和励磁电感来代替变换器的谐振电感和激磁电感,减小变换器体积,提高其功率密度
1.3.2 全桥LLC谐振变换器的工作原理(ZVS/ZCS)
LLC谐振变换器在调频工作方式下,通过改变开关频率的大小来调节其能 量输出的大小。根据开关频率fs与谐振频率fr的大小关系,LLC谐振变换器存在以下三种工作模式:

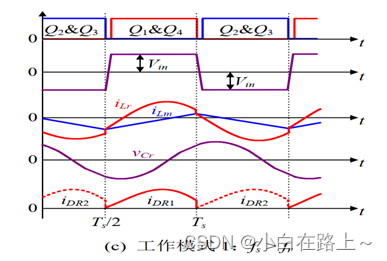
图 1.4 全桥LLC三种工作模式波形图
工作模式 1:fs < fr,此时变换器的主要工作波形如图1.4(a)所示。该模式下,当谐振电感电流iLr谐振到与励磁电感电流iLm相等时,如图中[t2~t4]所示,此时励磁电感Lm参与谐振,整流二极管电流断续,因此整流二极管可以实现ZCS关断。
工作模式 2:fs = fr,主要工作波形如图1.4(b)所示。励磁电感Lm不再参与谐振,其两端电压一直被输出电压箝位在nVo。整流二极管电流临界连续,因此同样能够实现ZCS关断。
工作模式 3:fs > fr,工作波形如图 1.4©所示。该模式下励磁电感Lm不参与谐振,其两端电压一直被箝位在 nVo。整流二极管电流连续,工作在硬关断模式下,因此存在反向恢复问题。
变换器在一个开关周期内共有6个模态,下图给出了各开关模态的等效电路图。
由于工作模式1中包含了模式2和模式3的工作模态,同时当LLC谐振变 换器工作在 fm<fs< fr的工作模式时,即能实现原边开关管的ZVS,也能实现整流二极管的ZCS。因此本文以工作模式1为例,分析变频模式时全桥LLC谐振变换器的工作原理。
在分析之前作如下假设:
-
所有开关管和二极管均为理想器件,所有电感、电容和变压器均为理想元件;
-
开关管Q1~Q4的结电容C1 = C2 = C3 = C4 = Coss;
-
输出滤波电容足够大,近似认为是一个大小为Vo的电压源。
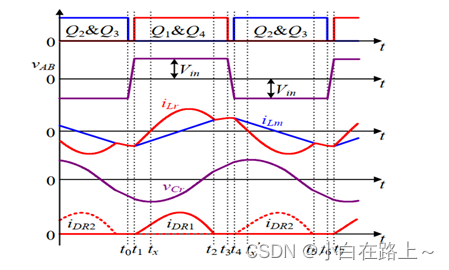
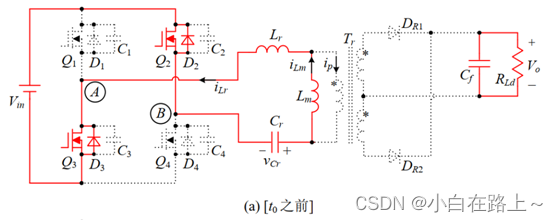
图 1.5
1)开关模态0 [t0之前],对应图t0时刻之前,开关管Q2和Q3导通,Lr、Cr
和 Lm 组成的谐振回路共同谐振。整流二极管DR1和DR2反偏截止,输出被变 压器隔离。变压器原、副边均无电流,输出电容Cf给负载供电。

图 1.6
2)开关模态1[t0,t1],对应图t0时刻,关断开关管Q2和Q3,由于励磁电感 Lm较大且该模态持续时间很短,可以近似认为谐振电感电流不变,iLr=iLm =Im,给C2和C3充电,同时给C1和C4放电。当Q1和Q4的体二极管导通时,即可零电压开通Q1和Q4。为了保证开关管Q1和Q4的零电压开通,应在iLr 由负变正之前开通Q1和Q4。

图 1.7
3)开关模态 2 [t1,t2],对应图t1时刻,零电压开通Q1和Q4。此时,A、B
两端的电压为Vin,整流二极管DR1导通,则励磁电感被箝位在nVo,不参与谐 振,励磁电感电流线性增加。Lr和Cr谐振工作,Lr和 Cr谐振网络两端的电压为(Vin−nVo)。
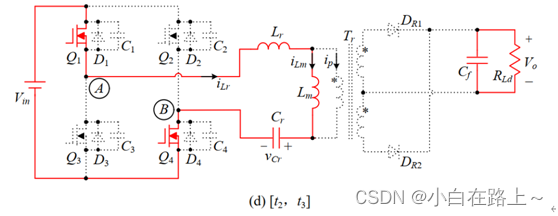
图 1.8
4)开关模态 3 [t2,t3],对应图t2时刻,谐振电感电流谐振到与励磁电感电 流相等,此时变换器负载端与谐振网络脱开,整流二极管DR1为ZCS关断,不 存在反向恢复问题。励磁电感 Lm 两端的电压不再被箝位在nVo,Lr、Lm与Cr 谐振工作。实际Lm一般比Lr大得多,所以该时段内谐振周期较长,可近似认为该时段内谐振电感电流保持不变,谐振电容被恒流充电,其两端电压线性上升。
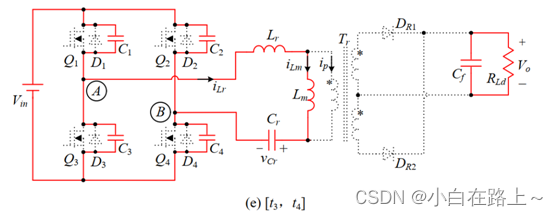
图 1.9
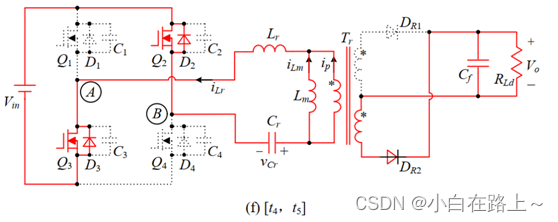
图 1.10
t3时刻开始,关断Q1和Q4,进入下半个工作周期,变换器的工作原理与上半个周期工作情况类似,这里将不再赘述。
1.3.3 全桥LLC谐振变换器的基本特性分析(基波分析法)
本节将采用基波分析法分析LLC谐振变换器的特性。一个完整的全桥LLC 谐振变换器的主电路结构如所示,将变换器的主电路模块化后,可以将其划分为: 逆变网络,谐振网络和整流滤波网络。
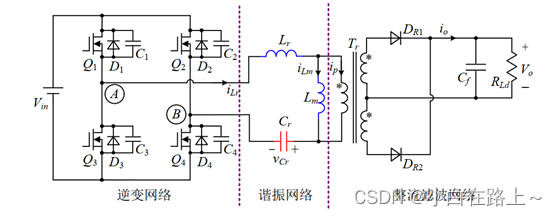
图 1.11 功能结构图
全桥LLC谐振变换器中开关管Q1&Q4与开关管Q2&Q3交替互补导通,则 A、B 两端的电压是一幅值为Vin的方波电压,如图所示。VAB傅立叶级数展开后的表达式为:

VAB的及其基波分量如图所示,根据基波分析法的思想,其VAB可以用其基波分量VAB1代替。

图 1.12 基波分析法
当LLC谐振变换器工作在谐振频率点附近时,整流滤波网络的输入电流可以近似认为是一正弦基波分量,其表达式为:

当ip> 0 时,整流二极管DR1导通,变压器原边电压vp =nVo,is=n∙ip
当ip< 0时,整流二极管DR2导通,变压器原边电压vp =-nVo,is=−n∙ip。ip(t)、is(t)、vp(t)以及io(t)的波形如图1.13所示。对其傅立叶分解后,可以得到变压器原边电压的基波分量为:
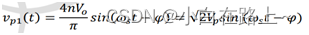
其中,Vp1为原边电压基波分量的有效值,大小为:

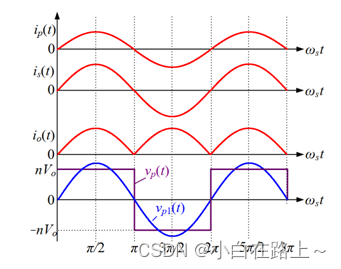
图 1.13 电流波形
整流网络的电流经过输出滤波电容Cf后,高频分量被滤除,所以只有直流分量流过负载电阻RLd,大小等于Io,则有:

因此可以得到:
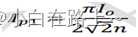
由可知整流网络可以等效为一纯阻性电阻:

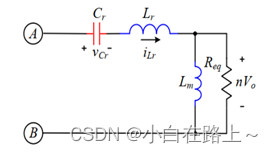
图 1.14 LLC 等效电路




![[个人感悟] MySQL应该考察哪些问题?](https://img-blog.csdnimg.cn/direct/3f01cb100b09427994ea5d60f7395be1.png#pic_center)






![【计算机网络】[第4章 网络层][自用]](https://img-blog.csdnimg.cn/direct/45e73d08c6614a32b73427f3ff22e7c7.png)