DDP(Differential Dynamic Programming)算法
基本原理
- DDP(Differential Dynamic Programming)是一种用于求解非线性最优控制问题的递归算法。它基于动态规划的思想,通过线性化系统的动力学方程和二次近似代价函数,递归地优化控制策略。DDP的核心在于利用局部二次近似来简化全局非线性最优控制问题,从而高效地求解控制策略。
- DDP算法通过递归的方式,结合局部线性化和二次近似,高效地求解非线性最优控制问题。它适用于多种机器人控制场景,特别是对于动态系统的控制问题具有良好的适应性。在实际应用中,DDP的初始解选择和收敛性可能需要进一步调整和优化。
算法步骤
1、初始化:
- 给定初始状态 x0。
- 初始化控制序列 {𝑢0,𝑢1,…,𝑢𝑇−1}。
- 设置最大迭代次数和收敛准则。
2、前向传播(Forward Pass):
- 通过给定的控制序列 {𝑢k},从初始状态 x0开始,依次计算系统状态 {x𝑘}:
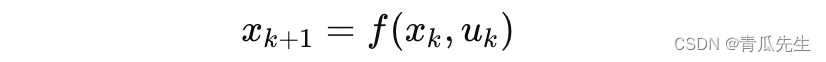
- 计算总代价 J: