什么是堆?
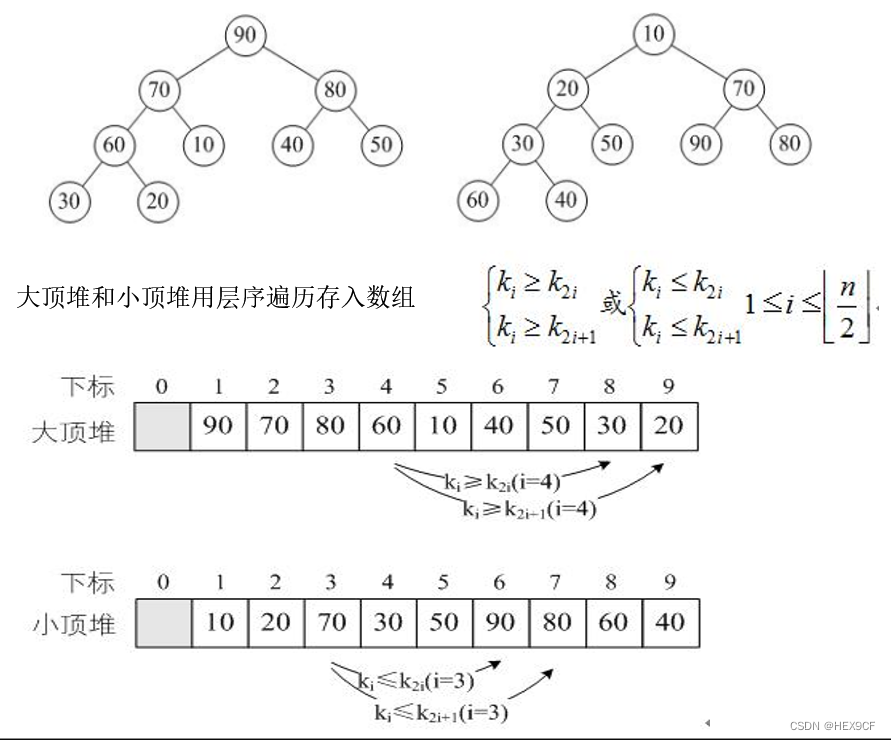
堆是一种特殊的完全二叉树,它满足堆的性质:在最大堆中,对于除了根之外的每个节点i,都有A[parent(i)] >= A[i];在最小堆中,对于除了根之外的每个节点i,都有A[parent(i)] <= A[i]。在最大堆中,父节点的值总是大于或等于其子节点的值;在最小堆中,父节点的值总是小于或等于其子节点的值。



建堆过程。
-
初始化堆:首先,将待排序的序列看作是一个完全二叉树(数组的形式存储),从最后一个非叶子节点开始(即最后一个节点的父节点),将当前节点和其子节点进行比较,如果当前节点小于(或大于,取决于是建立最大堆还是最小堆)其子节点,则交换它们。然后,向上移动到前一个非叶子节点,重复这个过程,直到根节点。
-
调整堆:初始化堆之后,根节点可能不满足堆的性质(在最大堆中,父节点应大于子节点;在最小堆中,父节点应小于子节点)。此时,我们需要调整堆。从根节点开始,将其与子节点进行比较并交换(如果需要),然后递归地调整子节点。这个过程一直持续到叶子节点,确保所有节点都满足堆的性质。
void push(int x) {hmin[++cnt] = x;int p = cnt;// 上浮while (p) {int parent = p >> 1;if (hmin[parent] > hmin[p]) {swap(hmin[parent], hmin[p]);} else {break;}p = parent;}return;
}




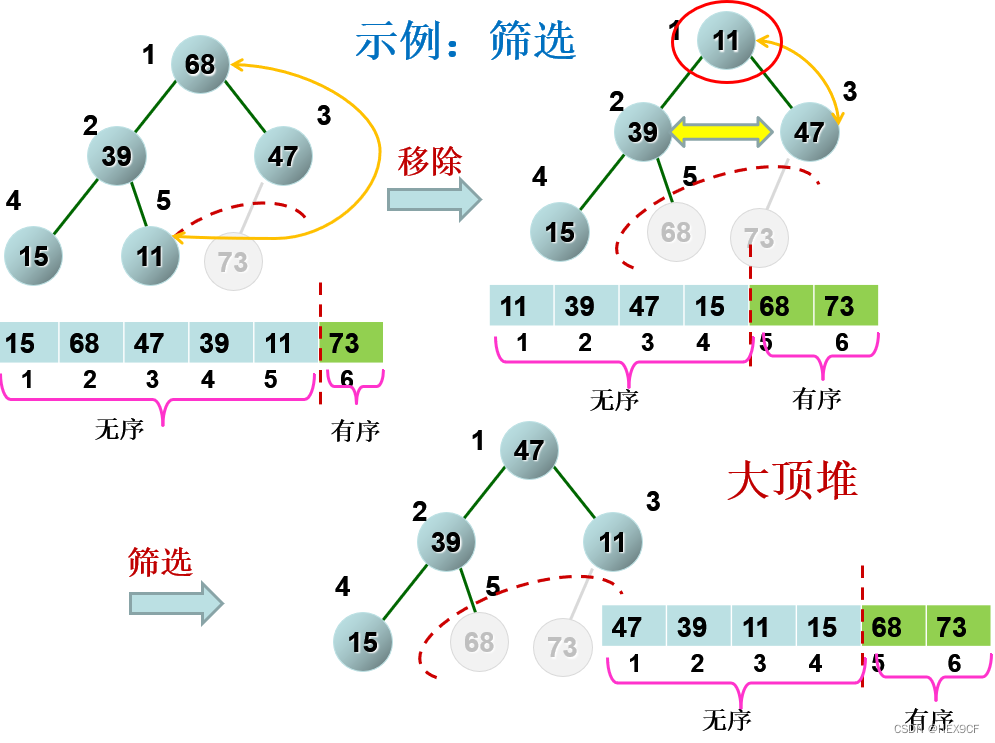
取出堆顶元素。
void pop() {swap(hmin[1], hmin[cnt--]);int p = 1;// 下沉while ((p << 1) <= cnt) {int child = p << 1;int childr = child + 1;if (childr <= cnt && hmin[child] > hmin[childr]) {// 右孩子更小child = childr;}if (hmin[child] < hmin[p]) {swap(hmin[child], hmin[p]);} else {break;}p = child;}return;
}