大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

抱个拳，送个礼

1. 方差

方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在数据分析和机器学习中，方差常用于描述数据集的变异情况

1.1 定义与计算方法 方差的计算方法如下：

1. 计算数据集的均值（平均值）
2. 计算每个数据点与均值的差值
3. 将这些差值平方
4. 将平方后的差值相加
5. 将总和除以数据点的数量

方差的公式为：

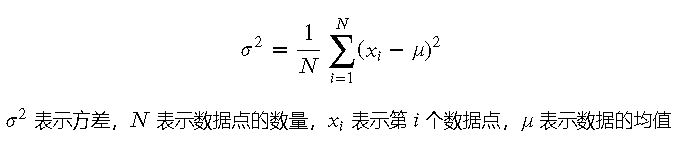
1.2 实际应用 方差在许多领域都有广泛应用。例如，在金融领域，方差用来衡量投资回报率的波动性。在质量控制中，方差用来衡量生产过程的稳定性。在机器学习中，方差用于评估模型的性能和稳定性

1.3 示例

假设我们有一组数据：[1, 2, 3, 4, 5]

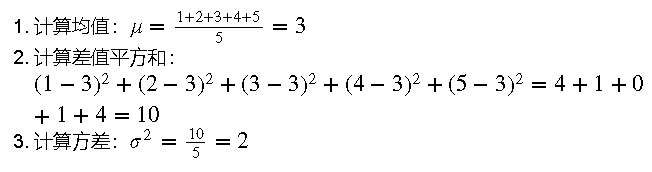
2. 标准差

标准差是方差的平方根，是另一种度量数据分散程度的指标。标准差与方差一样，反映了数据点与均值之间的偏离程度，但标准差的单位与数据本身一致，因此更容易解释和理解

2.1 定义与计算方法 标准差的计算方法如下：

1. 计算数据集的均值（平均值）
2. 计算每个数据点与均值的差值
3. 将这些差值平方
4. 将平方后的差值相加
5. 将总和除以数据点的数量，得到方差
6. 对方差取平方根，得到标准差

标准差的公式为：

2.2 实际应用 标准差广泛应用于各种领域。例如，在金融领域，标准差用来衡量投资回报率的波动性。在质量控制中，标准差用来衡量生产过程的稳定性。在统计分析和数据科学中，标准差用来描述数据集的离散程度

2.3 示例

继续前面的例子，假设我们有一组数据：[1, 2, 3, 4, 5]

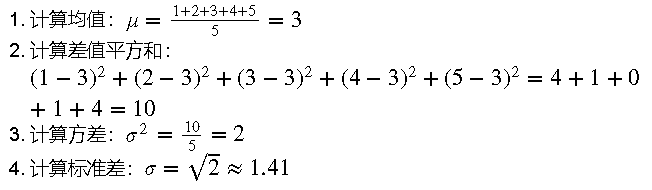
防失联，进免费知识星球，直达算法金 AI 实验室 https://t.zsxq.com/ckSu3

更多内容，见免费知识星球

3. 协方差

协方差是用来衡量两个变量之间关系的一种统计指标。它表示了两个变量如何一起变化：当一个变量变大时，另一个变量是否也变大（正协方差）或变小（负协方差）。协方差的值可以是正、负或零，具体取决于变量之间的关系

3.1 定义与计算方法 协方差的计算方法如下：

1. 计算每个变量的均值（平均值）
2. 计算每个变量与其均值的差值
3. 将两个变量的差值乘积求和
4. 将和除以数据点的数量

协方差的公式为：

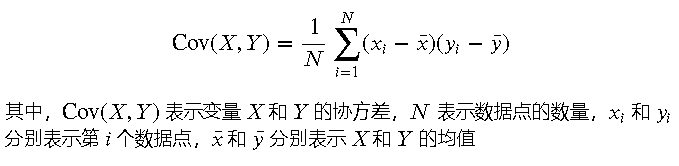
3.2 实际应用 协方差在许多领域都有广泛应用。例如，在金融领域，协方差用来衡量不同资产回报率之间的相关性。在经济学中，协方差用来分析不同经济指标之间的关系。在机器学习中，协方差用于特征选择和数据预处理

3.3 示例

假设我们有两个变量的数据集：𝑋=[1,2,3,4,5]𝑋=[1,2,3,4,5] 和 𝑌=[2,4,6,8,10]

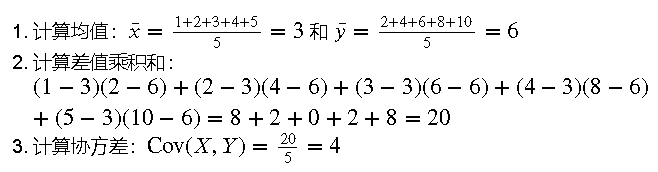
抱个拳，送个礼

点击 ↑ 领取

4. 协方差矩阵

协方差矩阵是用于描述多个变量之间协方差关系的矩阵。它是一个对称矩阵，其中每个元素表示对应变量对之间的协方差。协方差矩阵在多变量统计分析和机器学习中起着重要作用

4.1 定义与计算方法 协方差矩阵的计算方法如下：

1. 计算每个变量的均值（平均值）
2. 计算每个变量与其均值的差值
3. 计算每对变量之间的协方差
4. 将协方差填入矩阵对应位置

协方差矩阵的公式为：

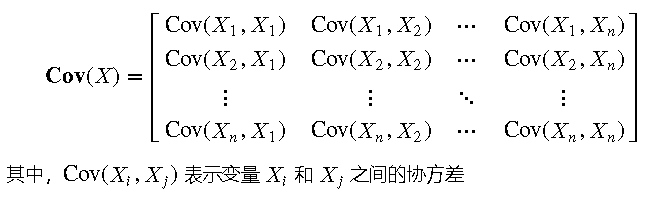
4.2 实际应用 协方差矩阵在数据分析和机器学习中有广泛的应用。例如，在主成分分析（PCA）中，协方差矩阵用于特征降维。在多变量回归分析中，协方差矩阵用于估计回归系数的标准误。在组合投资中，协方差矩阵用于分析不同资产的风险

4.3 示例

假设我们有三个变量的数据集：𝑋1=[1,2,3]，𝑋2=[4,5,6]，𝑋3=[7,8,9]

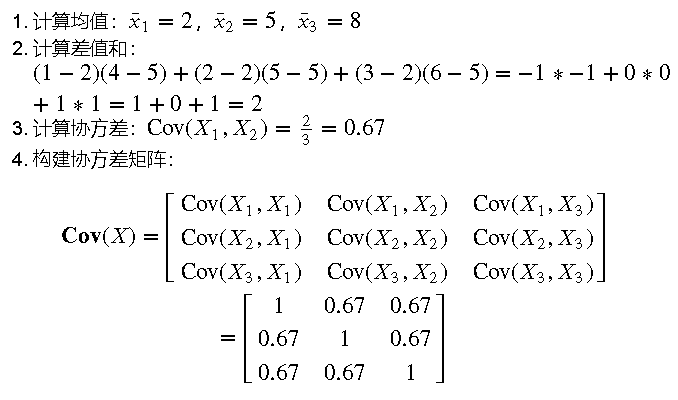
防失联，进免费知识星球，直达算法金 AI 实验室

https://t.zsxq.com/ckSu3

5. 各指标之间的关系与对比

在数据分析和统计学中，方差、标准差、协方差及协方差矩阵都是衡量数据分布和变量关系的重要工具。理解它们之间的关系和区别有助于更好地应用这些工具进行分析

5.1 方差与标准差 方差和标准差都是度量数据分散程度的指标，但它们的单位和解释不同

• 方差：方差表示数据点与均值之间的平方差的平均值，单位是数据单位的平方。方差公式为：

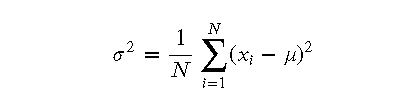
• 标准差：标准差是方差的平方根，因此其单位与数据本身一致。标准差公式为：

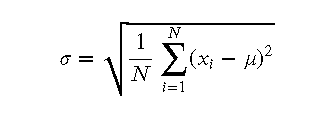
5.2 标准差与协方差 标准差和协方差虽然都是度量数据分布和关系的指标，但它们用于不同的情景

• 标准差：标准差用于度量单个变量的分散程度，是方差的平方根。它可以帮助我们理解单个变量的波动性
• 协方差：协方差用于度量两个变量之间的关系，表示一个变量变化时另一个变量的变化情况。协方差公式为：

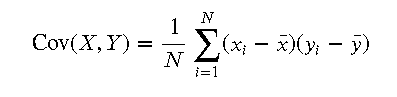
5.3 协方差与协方差矩阵 协方差和协方差矩阵都是用来描述变量之间关系的工具，但协方差矩阵可以同时描述多个变量之间的关系

• 协方差：协方差只描述两个变量之间的关系，正值表示正相关，负值表示负相关
• 协方差矩阵：协方差矩阵是一个对称矩阵，包含多个变量之间的协方差信息，用于多变量统计分析。协方差矩阵公式为：

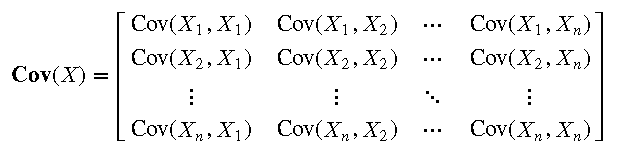
[ 抱个拳，总个结 ]

- 科研为国分忧，创新与民造福 -

日更时间紧任务急，难免有疏漏之处，还请大侠海涵 内容仅供学习交流之用，部分素材来自网络，侵联删

[ 算法金，碎碎念 ]

入选 CSDN 算法领域

内容榜单 Top 1

真香~

全网同名，日更万日，让更多人享受智能乐趣

如果觉得内容有价值，烦请大侠多多 分享、在看、点赞，助力算法金又猛又持久、很黄很 BL 的日更下去；同时邀请大侠 关注、星标 算法金，围观日更万日，助你功力大增、笑傲江湖