【简易版tinySTL】红黑树- 定义, 插入, 构建

文章目录

- 旋转
- - 左旋
  - 右旋
- 左旋右旋代码实现
- 红黑树的基本性质
- 红黑树的插入
- 红黑树的插入示例
- 红黑树修复代码实现
- 参考资料

旋转

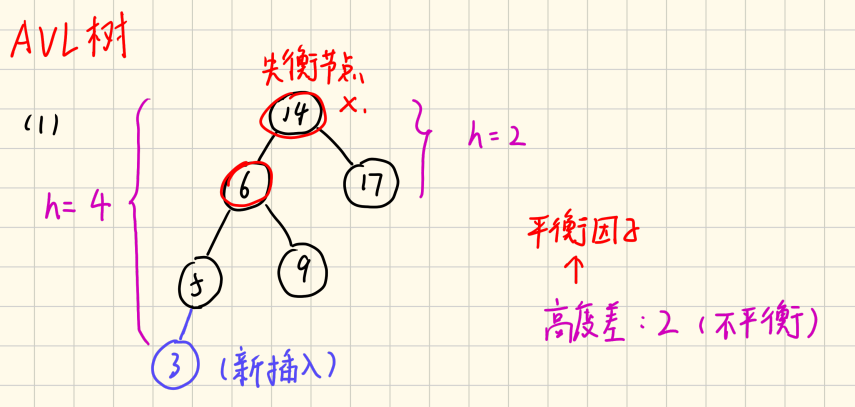
对于一个平衡二叉搜索树，左子树高度为4，右子树高度为2，它们的高度差为2，破坏了平衡性（高度差<2才算平衡，因此需要调整二叉树使其平衡）

二叉树最基本的调整方式包括左旋、右旋：

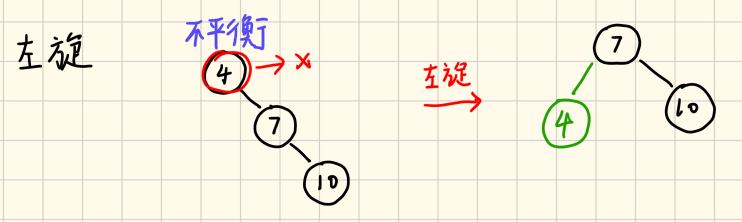
左旋

不平衡点没有左子树

不平衡点有左子树

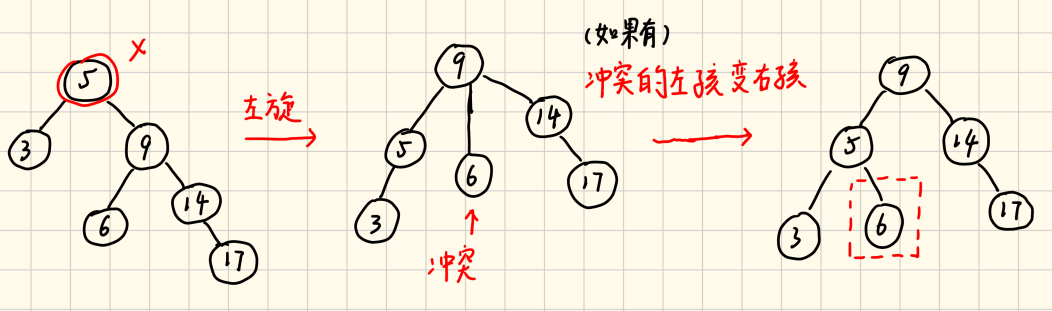
当结点5左旋时，由于有左子树3，会和结点6冲突，阻碍旋转，我们需要将"冲突的左孩变右孩"，即将结点6连在被旋转点5的右孩子上

右旋

不平衡点没有右子树

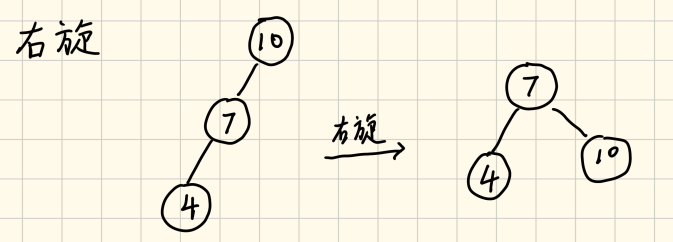
不平衡点有右子树

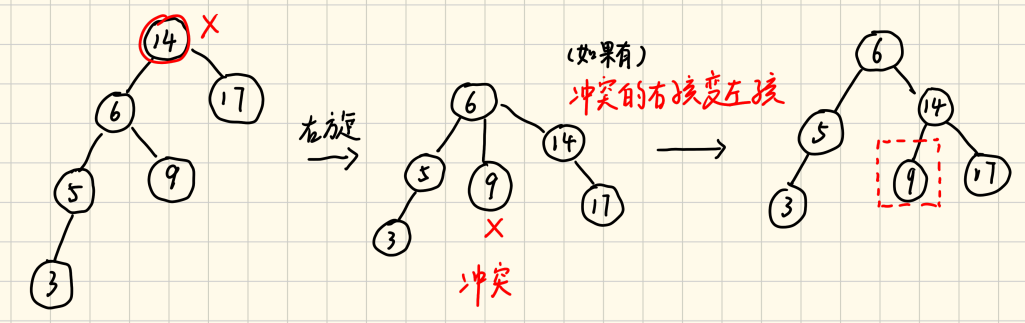
当结点14右旋时，由于有右子树17，会和结点9冲突，阻碍旋转，我们需要将"冲突的右孩变左孩"，即将结点9连在被旋转点14的左孩子上

左旋右旋代码实现

Node* rightRotate(Node* node)
{// node为失衡节点Node* l_son = node->left;// 不管是否会发生冲突，都把冲突的右孩变左孩node->left = l_son->right;// 右孩变左孩后，更新父节点（前提它不是空节点）if(node->left){node->left->parent = node;}// 更新旋转中心的父节点指向l_son->parent = node->parent;// 如果当前节点（node）是根节点，则更新根节点为 l_sonif(l_son->parent == nullptr){root = l_son;}// 如果node是父结点的左子节点else if(node->parent->left == node){node->parent->left = l_son;}else{// 如果node是父结点的右子节点node->parent->right = l_son;}// 把node结点接在l_son右边node->parent = l_son;l_son->right = node;return l_son;
}Node* leftRotate(Node* node)
{Node* r_son = node->right;// 提前断掉右结点node->right = r_son->left;if(r_son->left){node->right = r_son->left;r_son->left->parent = node;}r_son->parent = node->parent;if(r_son->parent == nullptr){root = r_son;}else if(node->parent->left == node){node->parent->left = r_son;}else{node->parent->right = r_son;}r_son->left = node;node->parent = r_son;return r_son;
}

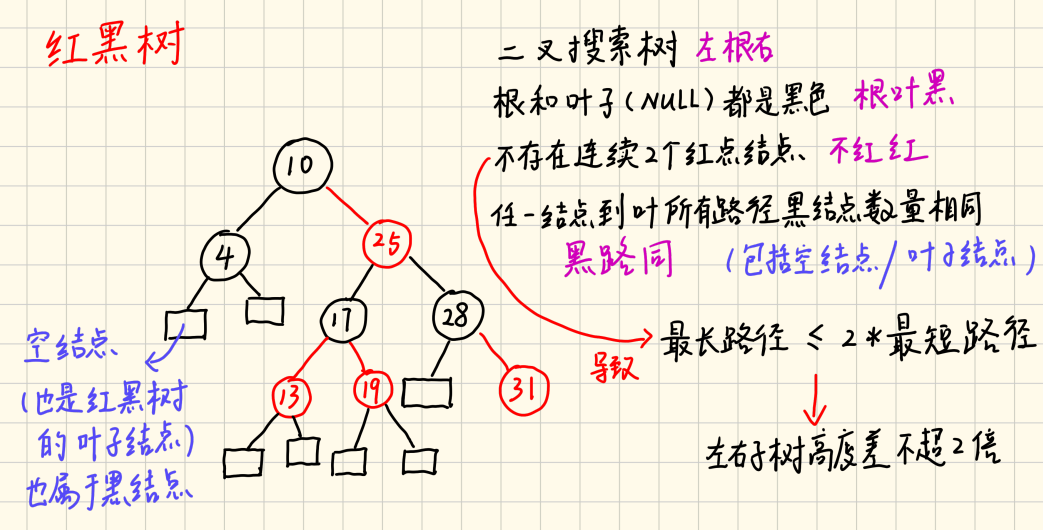
红黑树的基本性质

空结点也是红黑树的叶子结点，也属于黑结点

根叶黑：根和叶子结点默认为黑色
不红红：不存在连续2个红色结点
黑路同：任一结点到叶子结点的所有路径，黑结点的数量相同（包括空结点/叶子结点）

红黑树的插入

要求：

默认插入的都是红色
插入情况讨论：
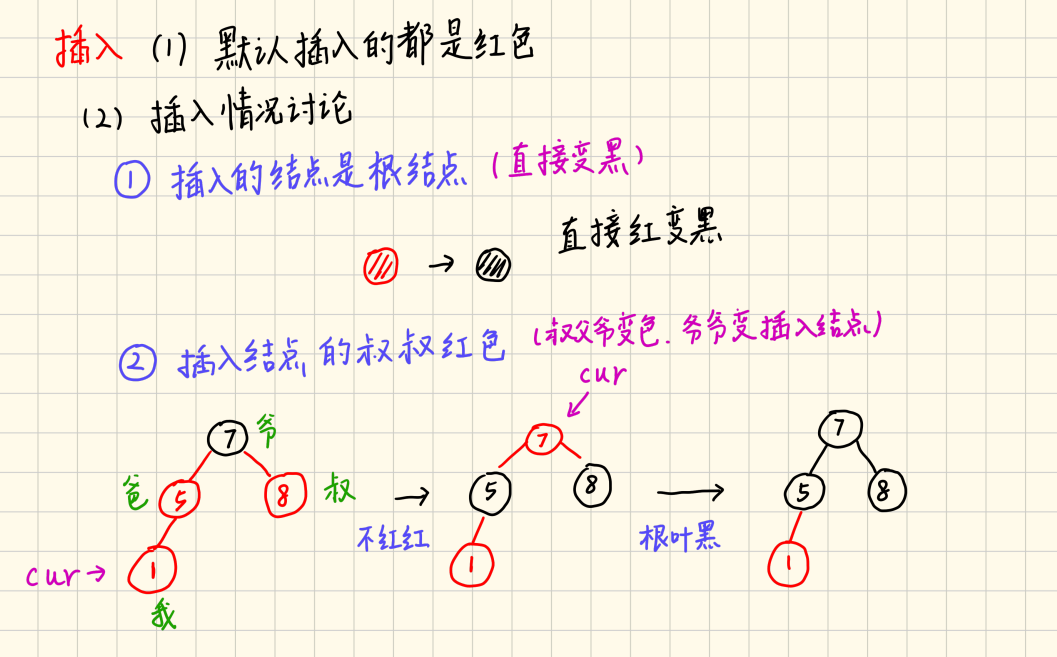
- 插入的结点是根结点：直接变黑
- 插入结点的叔叔结点是红色：叔父爷变色，当前指针指向爷爷结点，修复爷爷结点的红黑树性质
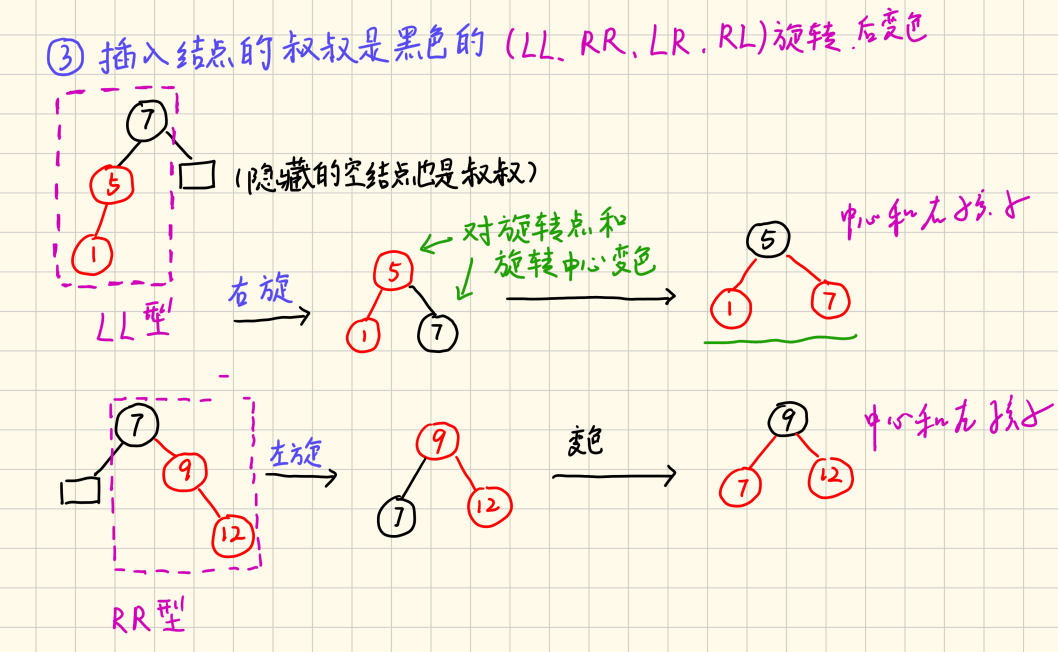
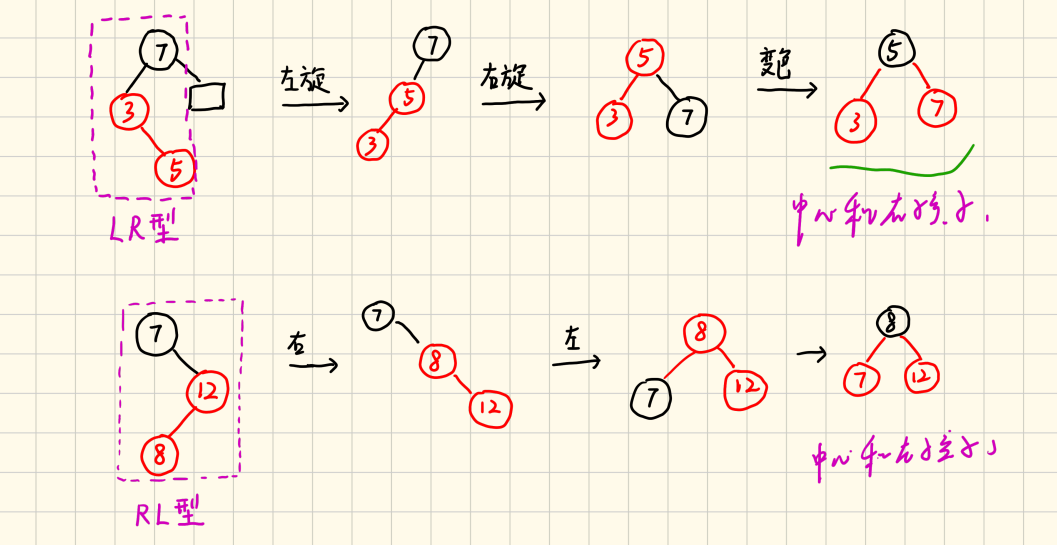
- 插入结点的叔叔结点是黑色：先旋转（LL、RR、LR、RL），后变色

红黑树的插入示例

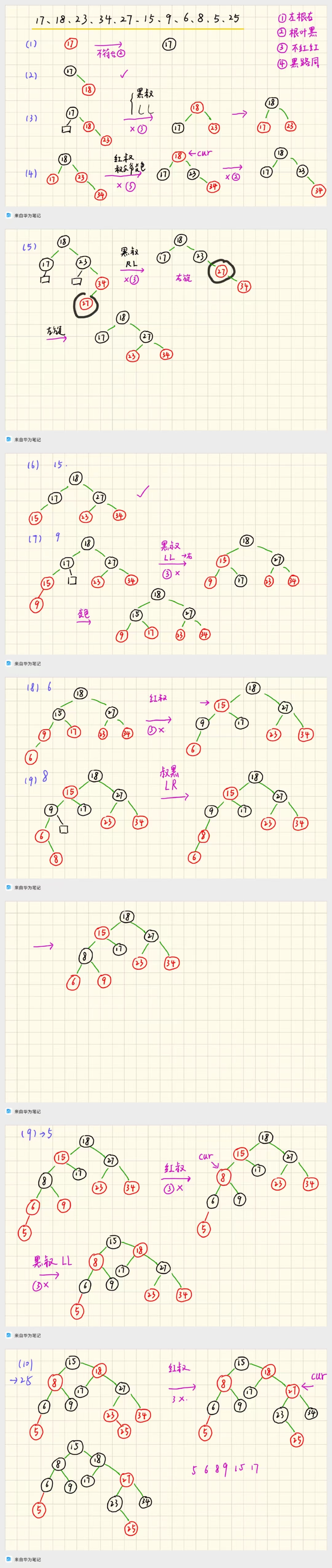
假设我们要依次插入：17、18、23、34、27、15、9、6、8、5、25

我们每次插入之后，都要检查是否满足红黑树的性质

微信图片_20240620192221

红黑树修复代码实现

/*O/O /O	<= target
*/
void insertFixup(Node* target) // target是当前插入的结点
{// 父结点存在，且出现红红while(target->parent && target->parent->color == Color::RED){Node* father = target->parent;Node* g_father;if(father)g_father = father->parent;// 父是爷的左孩子if(g_father && g_father->left == father){Node* uncle = g_father->right;// 如果叔结点存在，且颜色为红色if(uncle && uncle->color == Color::RED){// 叔父爷变色uncle->color = Color::BLACK;father->color = Color::BLACK;g_father->color = Color::RED;// 将当前指针指向爷结点target = g_father;}// 叔结点不存在或者颜色为黑色(LL/LR)else{// LRif(target == g_father->left->right){// 先左旋，旋转函数的输入结点是失衡点leftRotate(father);}// RR和LR后面的步骤都是一样的Node* t = rightRotate(g_father);// 变色t->color = Color::BLACK;t->right->color = Color::RED;t->left->color = Color::RED;return;}}if(g_father && g_father->right == father){Node* uncle = g_father->left;if(uncle && uncle->color == Color::RED){g_father->color = Color::RED;father->color = Color::BLACK;uncle->color = Color::BLACK;target = g_father;}else{// RLif(target == g_father->right->left){// !不是旋转父结点rightRotate(father);}// LL和RL后续都一样Node* t = leftRotate(g_father);t->color = Color::BLACK;t->left->color = Color::RED;t->right->color = Color::RED;return;}}root->color = Color::BLACK;}
}void insert(Key k, Value v)
{Node* node = new Node(k, v);Node* p = nullptr;Node* cur = root;if(this->size == 0){root = node;size++;return;}// 找到插入点while(cur){p = cur;if(k > cur->key){cur = cur->right;}else if(k < cur->key){cur = cur->left;}else{std::cout << "the key was in the tree" << std::endl;delete node;return;}}// 插入新结点size++;if(k > p->key){p->right = node;}else{p->left = node;}node->parent = p;if(!p){root = node;}// 修复红黑树insertFixup(node);
}