INS-GPS组合导航——卡尔曼滤波

系列文章目录

《SAR笔记-卫星轨道建模》

《SAR笔记-卫星轨迹（三维建模）》

《常用坐标系》

文章目录

前言

一、经典卡尔曼滤波

二、扩展卡尔曼滤波

三、无迹卡尔曼滤波

总结

前言

SAR成像仪器搭载于运动平台，平台的自定位误差将影响SAR图像质量。为保证SAR成像质量，需要长期精确且稳定的平台自定位轨迹，目前常见的定位系统包括惯导系统以及卫导系统。

惯性导航系统INS测量角度增量、速度增量等惯导参量，通过路径积分得到平台的位置、速度、姿态信息，具有较高的短期测量精度，更新频率高，但惯导数据漂移，长期导航误差大。全球定位系统GPS通过测量不同卫星与平台的时延差估计平台位置，具有良好的长期精度，但短期精度差，数据输出频率低，受星座构型、环境影响大。惯导系统测量量与卫导系统测量量之间相互联系，都能生成平台轨迹数据，但测量是相互独立的，因此可以用两套系统测得的数据进行融合，得到长期短期的稳定度以及精度都很高的平台轨迹信息。其中一种常见的数据融合算法就是卡尔曼滤波。

卡尔曼滤波本质上是一个数据融合算法，将具有同样测量目的、来自不同传感器、可能具有不同单位 (unit) 的数据融合在一起，得到一个更精确的目标估计值。本文简单介绍卡尔曼滤波的关键步骤，方便使用，关于步骤由来不做说明，网上的资料挺多的，可以根据自身需要学习。

一、经典卡尔曼滤波

经典卡尔曼滤波（Kalman Filter，KF）的局限性在于其只能拟合线性高斯系统。但其最大的优点在于计算量小，能够利用前一时刻的状态和当前时刻的测量值来得到当前时刻下的状态的最优估计。整个滤波算法主要涉及5个方程，分为两个阶段：预测阶段；校正阶段。

预测阶段涉及两个方程：

1、预测器方程（功能：由前一时刻的状态预测当前时刻的状态）

$\hat{x}_{n,n-1}=F\hat{x}_{n-1,n-1}+Gu_{n}$

2、预测器协方差方程（功能：得到当前状态估计的协方差）

$P_{n,n-1}=FP_{n-1,n-1}F^{T}+Q$

校正阶段涉及三个方程：

1、卡尔曼增益方程（功能：决定当前状态输出是更相信预测结果还是更相信测量结果）

$K_{n}=P_{n,n-1}H^{T}\left ( H P_{n,n-1}H^{T}+R_{n} \right )^{-1}$

2、状态更新方程（功能：卡尔曼滤波输出结果）

$\hat{x}_{n,n}=\hat{x}_{n,n-1}+K_{n}\left ( z_{n}-H \hat{x}_{n,n-1}\right )$

3、状态协方差更新（功能：更新状态的协方差更新）

$P_{n,n}=\left (I-K_{n} H\right )P_{n,n-1}\left (I-K_{n} H\right )^{T}+K_{n}R_{n}K_{n}^{T}$

除了上述主要方程，还涉及其他辅助方程：

1、测量方程（功能：描述状态量与测量量之间的关系）

$z_{n}=Hx_{n}$

考虑测量误差时，测量方程为

$z_{n}=Hx_{n}+v_{n}$

2、测量协方差（功能：描述测量量不确定性的，需要预先统计）

$R_{n}=E\left ( v_{n} v_{n}^{T}\right )$

3、过程噪声协方差（功能：描述系统建模误差，比如理论上匀速直线运动的模型，在实际处理中会因为各种干扰很难匀速直线，导致真实轨迹并非匀速直线运动，而预测器方程基于匀速直线模型建立，这样产生的误差即为过程噪声协方差 $w_{n}$ ，包括系统输入 $u_{n}$ 产生的影响，本文中 $w_{n}=Gu_{n}$ ，需要预先统计）

$Q_{n}=E\left ( w_{n} w_{n}^{T}\right )$

4、估计协方差（功能：卡尔曼滤波输出结果的协方差）

$P_{n,n}=E\left ( e_{n} e_{n}^{T}\right )=E\left ( \left ( x_{n} -\hat{x}_{n,n}\right ) \left ( x_{n} -\hat{x}_{n,n}\right ) ^{T}\right )$

其中更新后状态的协方差可以做如下化简

$P_{n,n}=\left (I-K_{n} H\right )P_{n,n-1}\left (I-K_{n} H\right )^{T}+K_{n}R_{n}K_{n}^{T}\\ =P_{n,n-1}-P_{n,n-1}H^{T}K_{n}^{T}-K_{n} HP_{n,n-1}+K_{n}\left (HP_{n,n-1}H^{T} +R_{n}\right )K_{n}^{T}\\ =P_{n,n-1}-P_{n,n-1}H^{T}K_{n}^{T}-K_{n} HP_{n,n-1}\\+P_{n,n-1}H^{T}\left ( H P_{n,n-1}H^{T}+R_{n} \right )^{-1}\left (HP_{n,n-1}H^{T} +R_{n}\right )K_{n}^{T}\\ =P_{n,n-1}-P_{n,n-1}H^{T}K_{n}^{T}-K_{n} HP_{n,n-1}+P_{n,n-1}H^{T}K_{n}^{T}\\ =P_{n,n-1}-K_{n} HP_{n,n-1}\\ =\left (I-K_{n} H \right )P_{n,n-1}\\$

这个方程看起来要精炼很多并且容易记忆，并且在许多情况下没什么问题。但是，在计算卡尔曼增益时的一个小误差（浮点截尾误差）可能给结果带来巨大的偏差。 $\left (I-K_{n} H \right )$ 的差可能因为浮点计算误差而使其结果不再是对称阵。这个方程在数值计算上并不稳定！

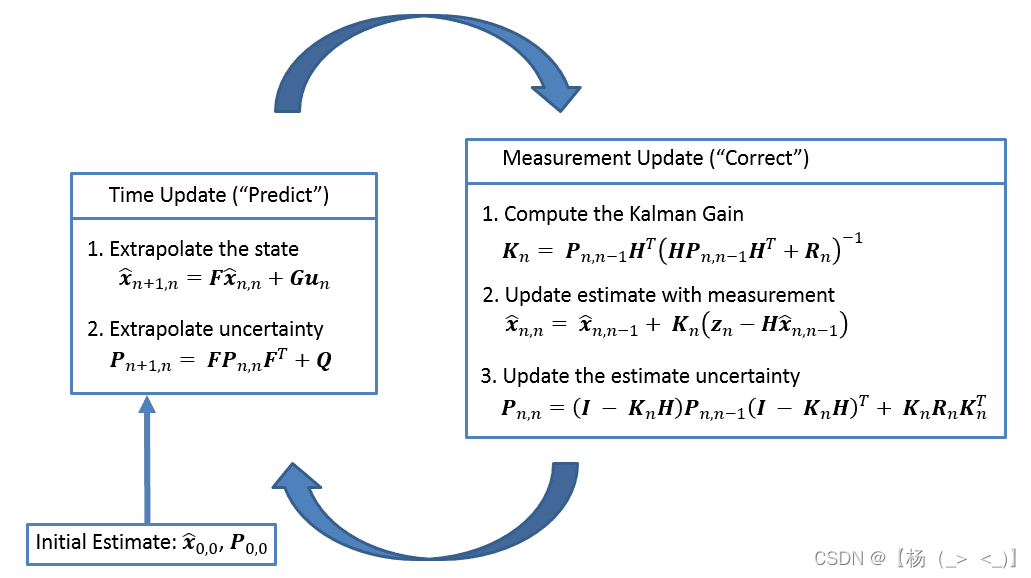
卡尔曼滤波算法流程如上图所示：一旦初始化完成，卡尔曼滤波首先预测下一时刻的系统状态，并且同时给出这个预测的不确定性。随后拿到测量结果，卡尔曼滤波会更新（或修正）这个预测值及其不确定性，并且同时再进行下一时刻的预测，以此类推。

二、扩展卡尔曼滤波

经典卡尔曼滤波解决的是经典的线性高斯系统的滤波问题。针对非线性系统，由于线性变换的关系不在了，因此预测量以及估计量的概率分布也不再是高斯分布。为了解决这类问题，人们利用非线性函数的局部线性特性，发明了扩展卡尔曼滤波（Extended Kalman Filter，EKF）。不考虑过程噪声以及噪声误差，非线性的状态转移方程以及观测为：

$x_{n}=f\left ( x_{n-1} \right )$

$z_{n}=h\left ( x_{n} \right )$

对函数f以及h进行泰勒展开并保留线性部分得

$f\left ( \hat{x}_{n-1} \right )=f\left ( x_{n-1} \right )+F_{n}\left ( \hat{x}_{n-1}- x_{n-1}\right )$

$h\left ( \hat{x}_{n} \right )=h\left ( x_{n} \right )+H_{n}\left ( \hat{x}_{n}- x_{n}\right )$

将非线性系统通过泰勒展开转换为动态变化的线性系统，扩展卡尔曼滤波与经典卡尔曼滤波类似，也包括：预测阶段；校正阶段。

预测阶段涉及两个方程：

1、预测器方程（功能：由前一时刻的状态预测当前时刻的状态）

$\hat{x}_{n,n-1}=f\left (\hat{x}_{n-1,n-1} \right )+w_{n}$

2、预测器协方差方程（功能：得到当前状态估计的协方差）

$P_{n,n-1}=F_{n}P_{n-1,n-1}F_{n}^{T}+Q$

其中 $F_{n}=\frac{\partial f}{\partial x}|_{x=\hat{x}_{n-1,n-1}}$ ；

校正阶段涉及三个方程：

1、卡尔曼增益方程（功能：决定当前状态输出是更相信预测结果还是更相信测量结果）

$K_{n}=P_{n,n-1}H_{n}^{T}\left ( H_{n} P_{n,n-1}H_{n}^{T}+R_{n} \right )^{-1}$

其中 $H_{n}=\frac{\partial h}{\partial x}|_{x=\hat{x}_{n,n-1}}$

2、状态更新方程（功能：卡尔曼滤波输出结果）

$\hat{x}_{n,n}=\hat{x}_{n,n-1}+K_{n}\left ( z_{n}-H_{n} \hat{x}_{n,n-1}\right )$

3、状态协方差更新（功能：更新状态的协方差更新）

$P_{n,n}=\left (I-K_{n} H_{n}\right )P_{n,n-1}\left (I-K_{n} H_{n}\right )^{T}+K_{n}R_{n}K_{n}^{T}$

扩展卡尔曼（EKF）与经典卡尔曼（KF）的区别在于测量矩阵H的计算。EKF对非线性函数进行泰勒展开后，进行一阶线性化的截断，忽略了其余高阶项，进而完成非线性函数的近似线性化。正是由于忽略了部分高阶项，使得EKF的状态估计会损失一些精度。因此，EHF 能否成功应用取决于两个因素：被近似的函数的局部非线性化程度；概率分布自身的不确定度（协方差）。

三、无迹卡尔曼滤波

无迹卡尔曼滤波（Unscented Kalman Filter，UKF）是一种非线性滤波算法，能够有效地处理复杂非线性系统的状态估计问题。其核心思想是通过一组选定的 sigma 点来逼近系统运动的高斯分布，从而实现状态估计。UKF算法通过选取 sigma 点，将系统的非线性映射转化为一组线性运算，然后利用卡尔曼滤波的思想进行状态估计。无迹卡尔曼滤波不采用泰勒展开实现非线性系统线性化，而是采用无迹变换（Unscented Transform，UT）来处理均值和协方差的非线性传递问题。

参考资料

卡尔曼滤波（Kalman Filtering）——（1）递归算法

Kalman滤波通俗理解+实际应用

卡尔曼滤波：从入门到精通

无人驾驶技术入门（十八）| 手把手教你写扩展卡尔曼滤波器

卡尔曼滤波

总结

本文主要介绍了经典卡尔曼滤波、扩展卡尔曼滤波，个人认为可以按照上述算法流程编写对应算法。从目前了解的信息，一般认为无迹卡尔曼滤波比前面两种卡尔曼滤波在非线性模型中的应用效果更好，后续根据学习情况更新无迹卡尔曼滤波。另外注明，本文为博主学习卡尔曼滤波的学习记录，内容上如果存在问题，欢迎评论区指出。转载请附链接【杨（_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/365112.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！