拓扑排序[讲课留档]

拓扑排序

拓扑排序要解决的问题是给一个有向无环图的所有节点排序。

即在 $A OE$ 网中找关键路径。

前置芝士！

有向图：有向图中的每一个边都是有向边，即其中的每一个元素都是有序二元组。在一条有向边 $(u, v)$ 中，称 $u$ 是 $v$ 的直接前驱， $v$ 是 $u$ 的直接后继。
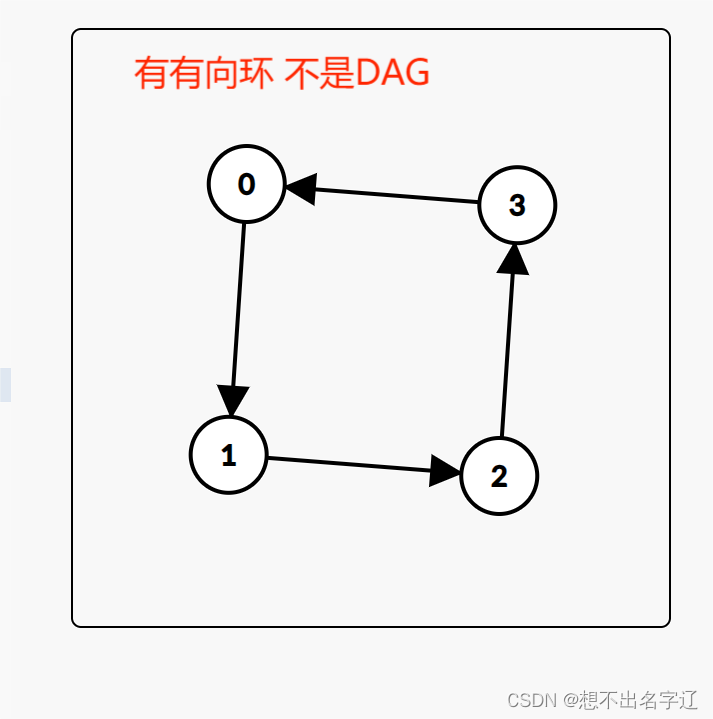
有向无环图 $(Directed\ Acyclic\ Graph)$ ：没有有向环，但不保证原图变成无向图时无环。

$D A G$ 的性质：能拓扑的图一定是 $D A G$ ， $D A G$ 一定能拓扑。( $A OE 和 A O V$ 网都是 $D A G$ )
度：顶点 $v$ 的度数是与 $v$ 关联的边数。有向图中没有度的概念。
入度、出度：入度是指以该顶点为终点的有向边数量；顶点的出度是指以顶点为起点的有向边数量。无向图中没有出入度的概念。

举个例子！

我们可以拿大学排课的例子来描述这个过程，比如学习大学课程中有：程序设计，算法语言，高等数学，离散数学，编译技术，数据结构，数据库系统等。当我们想要学习数据结构的时候，就必须先学会离散数学、编译技术和算法语言。

这些课程就相当于几个顶点 $u$ , 顶点之间的有向边 $(u, v)$ 就相当于学习课程的顺序。教务处安排这些课程，使得在逻辑关系符合的情况下排出课表，就是拓扑排序的过程。

但是如果某一天排课的老师打瞌睡了，说想要学习数据结构，还得先学操作系统，而操作系统的前置课程又是数据结构，那么到底应该先学哪一个（不考虑同时学习的情况）？在这里数据结构和操作系统间就出现了一个环，显然你现在没办法弄清楚你需要先学什么了，于是你也没办法进行拓扑排序了。

拓扑排序即，在一个 $D A G$ （有向无环图）中，我们将图中的顶点以线性方式进行排序，使得对于任何的顶点u到v的有向边 $(u, v)$ , 都可以有 $u$ 在 $v$ 的前面。

严谨来说，给定一个 $D A G$ ，如果从 $i$ 到 $j$ 有边，则认为 $j$ 依赖于 $i$ 。如果 $i$ 到 $j$ 有路径（ $i$ 可达 $j$ ），则称 $j$ 间接依赖于 $i$ 。拓扑排序的目标是将所有节点排序，使得排在前面的节点不能依赖于排在后面的节点。

理论存在！

从图中选择一个入度为零的点。
记录该顶点，从图中删除此顶点及其所有的出边。

重复上面两步，直到所有顶点都输出，拓扑排序完成，此时我们可以得到一个点的出队顺序（遍历顺序）这个序列叫拓扑序；或者图中不存在入度为零的点，此时说明图是有环图，拓扑排序无法完成。

拓扑排序需要遍历整张图，假设该图为 $G (V, E)$ ，获得拓扑序的时间复杂度大约是O（V+E）。

实践开始！

void topu_sort() {queue<int>q;for (int i = 1; i <= n; ++i) {if (!d[i])q.push(i);}while (!q.empty()) {int now = q.front();q.pop();ans.push_back(now);int len = vec[now].size();for (int i = 0; i < len; ++i) {int to = vec[now][i];d[to]--;if (!d[to]) q.push(to);}}/*for(auto x:vec[now]){d[x]--;if(!d[x]) q.push(x);}*/
}

例题

拓扑模板：B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 150;
int n;
vector<int> e[N];
int d[N];
vector<int> ans;void topu() {queue<int> q;for (int i = 1; i <= n; ++i) {if (d[i] == 0) q.push(i);}while (!q.empty()) {int now = q.front();q.pop();ans.push_back(now);for (auto x: e[now]) {d[x]--;if (d[x] == 0) q.push(x);}}
}int main() {cin >> n;for (int i = 1; i <= n; ++i) {int x;while (cin >> x) {if (x == 0) break;d[x]++;e[i].push_back(x);}}topu();for (auto x: ans) {cout << x << " ";}cout << '\n';return 0;
}

提高

拓扑构造：Problem - E - Codeforces

解析：

先忽略所有输入的无向边（但是不忽略点），对当前的有向图拓扑排序，如果给定的有向图中已经不是 $D A G$ 显然是一定不成立也无法构造的；如果当前的图是 $D A G$ ，那么拓扑完我们可以得到一个或多个拓扑序，每个拓扑序都是线性的，这也代表当选定一个拓扑序，在所有点中任选两个点，他们一定有已知确定先后顺序，我们按照这样的顺序去构造，建边（每次令拓扑序靠前的指向靠后的）即可保证不会出现拓扑序靠前的点依赖于靠后的点，则不会出现有向环。

AC代码：
pii ans[N];
vector<int>e[N];
int d[N];
int n,m,order=0;
int ord[N];bool topu(){queue<int>q;for(int i=1;i<=n;++i){if(!d[i]){q.push(i);}}while(!q.empty()){int t=q.front();q.pop();ord[t]=++order;for(auto x:e[t]){d[x]--;if(!d[x])q.push(x);}}if(order!=n)return 0;return 1;
}void work() {cin>>n>>m;int tot=0;order=0;for(int i=1;i<=n;++i){d[i]=0;e[i].clear();ans[i].fi=ans[i].se=0;}for(int i=1;i<=m;++i){int z,u,v;cin>>z>>u>>v;if(z){e[u].pb(v);d[v]++;}else{ans[++tot].fi=u;ans[tot].se=v;}}if(!topu()){cout<<"No\n";return;}cout<<"Yes\n";for(int i=1;i<=tot;++i){if(ord[ans[i].fi]>ord[ans[i].se])swap(ans[i].se,ans[i].fi);cout<<ans[i].fi<<" "<<ans[i].se<<'\n';}for(int i=1;i<=n;++i){if(e[i].size()){for(auto x:e[i]){cout<<i<<" "<<x<<'\n';}}}
}
课后练习：P1347 排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)