DP：子序列问题

文章目录

什么是子序列
- 子序列的特点
- 举例说明
- 常见问题
关于子序列问题的几个例题
- 1.最长递增子序列
- 2.摆动序列
- 3.最长递增子序列的个数
- 4.最长数对链
- 5.最长定差子序列
总结

什么是子序列

在计算机科学和数学中，子序列（Subsequence）是指从一个序列中删除一些元素（可以是零个或多个），但不改变其余元素相对顺序后形成的新序列。

子序列的特点

元素的相对顺序保持不变。
可以删除零个或多个元素。
一个序列的子序列可以为空序列，即不包含任何元素。

举例说明

设有序列 S = [A, B, C, D, E]，则其子序列可以有：
删除零个元素：[A, B, C, D, E]（即自身）
删除一个元素：[A, B, C, D]、[A, B, C, E]、[A, B, D, E]、[A, C, D, E]、[B, C, D, E]
删除两个元素：[A, B, C]、[A, B, D]、[A, B, E]、[A, C, D]、[A, C, E]、[A, D, E]、[B, C, D]、[B, C, E]、[B, D, E]、[C, D, E]
删除三个元素：[A, B]、[A, C]、[A, D]、[A, E]、[B, C]、[B, D]、[B, E]、[C, D]、[C, E]、[D, E]
删除四个元素：[A]、[B]、[C]、[D]、[E]
删除所有元素：[]（空序列）

常见问题

子序列问题在算法设计和编程竞赛中非常常见。以下是几种经典问题：
最长公共子序列（LCS）：给定两个序列，找出它们的最长公共子序列。动态规划是解决这个问题的常用方法。
最长递增子序列（LIS）：给定一个序列，找出其中最长的递增子序列。可以使用动态规划或贪心算法结合二分查找解决。
子序列和问题：给定一个序列，找出所有和为特定值的子序列。可以使用回溯法或动态规划解决。

根据我上面的介绍，可以总结，大多数子序列问题其实都可以用DP的算法来解决。

关于子序列问题的几个例题

1.最长递增子序列

题目链接
题目：

样例输出和输入：

首先根据上述子序列的描述，这道题就很容易理解了，就是让我们求给定数组的最长的递增子序列。
算法原理：
状态表示：dp[i]表示以i位置为结尾的所有子序列中最长的那个子序列的长度。
状态转移方程：
在这里插入图片描述
首先我们要求状态转移方程就要看i位置的状态，我们要确定i位置的状态，是不是应该将0到i-1位置遍历一遍，然后将当中的最长子序列求出来然后再加上当前位置的长度1就可以了，这是当子序列长度大于1的时候，还有一种情况是长度等于1的时候，长度等于1的时候，可以默认看做一个子序列，所以dp[i]就等于1，当长度大于1的时候，这种情况，我们先用一个变量j将0到i-1位置的最长子序列遍历出来，然后再+1，所以状态转移方程：dp[i] = max(dp[j]+1,dp[i])。
初始化：因为单独一个元素就可以看做一个递增的子序列，所以DP表中的值可以全部初始化为1.
代码展示：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i-1;j >= 0;j--){if (nums[j] < nums[i]){dp[i] = max(dp[j]+1,dp[i]);}dpmax=max(dp[i],dpmax);}}return dpmax;}
};

运行结果：
在这里插入图片描述

2.摆动序列

题目链接
题目：

样例输出和输入：

这道题让我们求摆动序列的最长的子序列的长度，首先我们要搞清楚，什么是摆动序列：
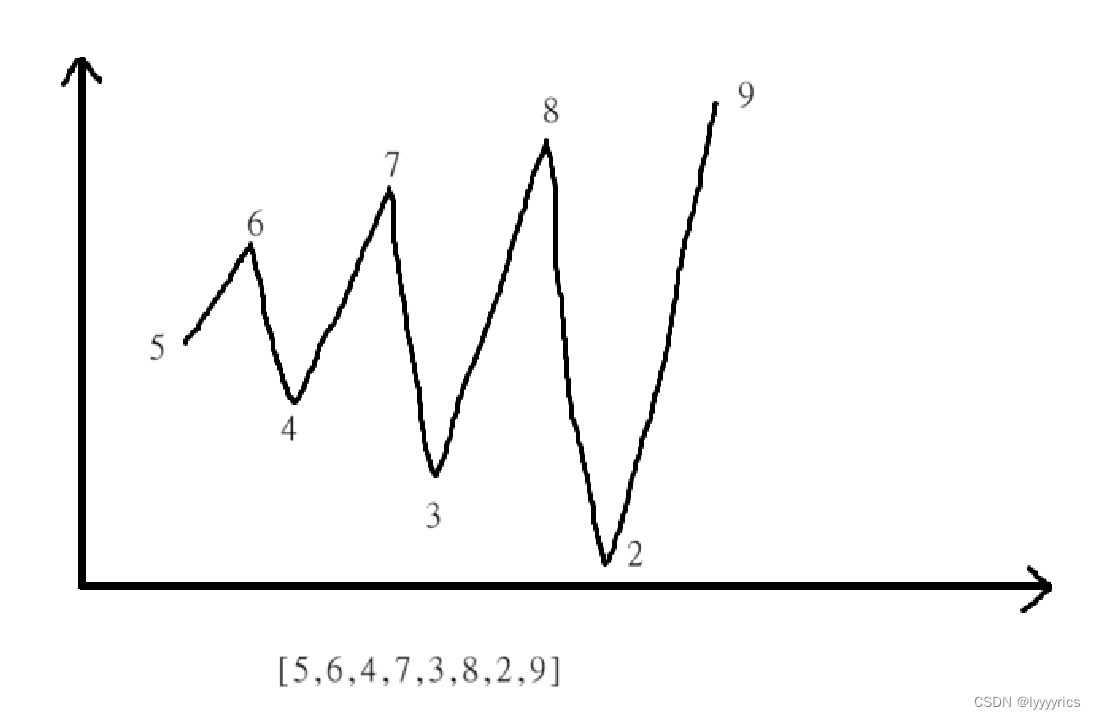
在这里插入图片描述

上面就是一个摆动序列。
算法原理：
这道题首先要求摆动序列，我们上个专题已经做过类似的题了，就像湍流数组一样，这道题很显然，我们需要两个状态，一个状态是向下的状态，一个状态是向上的状态，这里定义f[i]是向上的状态，g[i]是向下的状态。
状态表示：f[i]是以i位置为结尾的子序列中长度最长且最后一个状态是向上的最长子序列的长度，g[i]表示以i位置为结尾最后的子序列中最后一个状态向下的最长子序列的长度。
状态转移方程：首先对f[i]分析：在这里插入图片描述
所以这里f[i]的状态转移方程：f[i] = max(g[j] + 1, f[i])，同理也可以求出g[i]的状态转移方程：g[i] = max(f[j] + 1, g[i])
代码展示：

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n,1), g(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (nums[j] > nums[i]){g[i] = max(f[j] + 1, g[i]);}else if (nums[j] < nums[i]){f[i] = max(g[j] + 1, f[i]);}dpmax = max(max(dpmax, f[i]), g[i]);}}return dpmax;}
};

运行结果：
在这里插入图片描述

3.最长递增子序列的个数

题目链接
题目：

样例输出和输入：

这道题相对于第一道题换了一个问法。这道题是求最长子序列的个数
算法原理：
状态表示：首先我们先定义一个状态，看这个状态能推下去吗，dp[i]表示以i位置为结尾的所有子序列中，最长子序列的个数。
状态转移方程：首先这里就出问题了，这里我们根本不知道最长的子序列是什么，因为根本没有记录的，所以这里根本就推不出来，所以还得加一个len[i]，len[i]表示以i位置为结尾的所有子序列中最长子序列的长度，将dp[i]改为count[i]，count[i]表示以i位置为结尾的所有子序列中最长的子序列的个数。接下来来推状态转移方程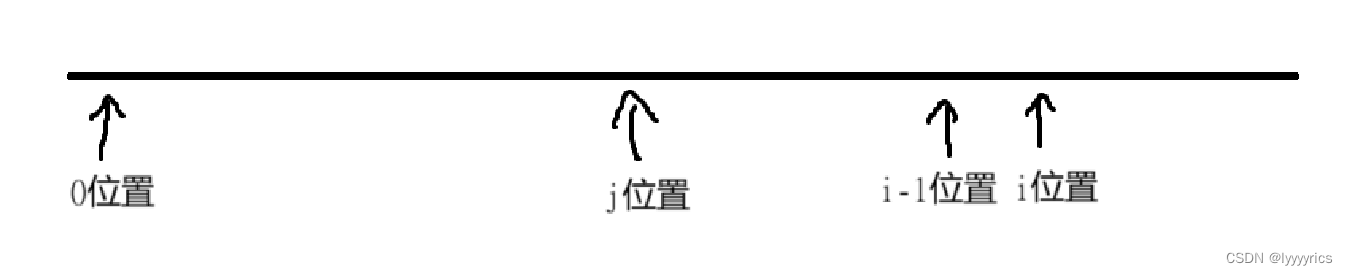，在这里插入图片描述
有三种情况，当我们遍历的len[j]+1==len[i]，意思就是0到i-1位置的子序列中加上当前的长度和之前的最长的子序列是相同的，这里我们应该把以j位置为结尾的最长子序列的个数全部加到count[i]]中。这里画图表示
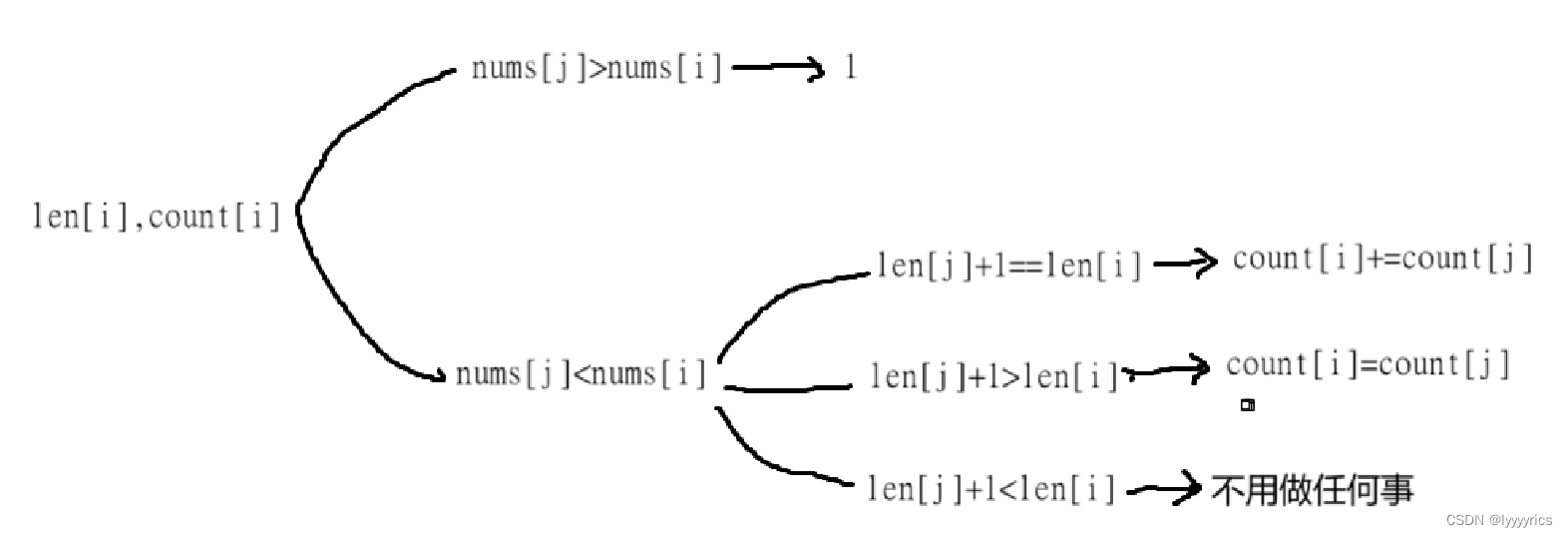
在这里插入图片描述

根据这些情况可以将表填完，但是，我们还需要一个retlen和一个retcount更新每次的最长子序列的长度和最长子序列的个数。
这里也分为三种情况，和上面的情况相同，只需要每次遍历完一个位置，更新结果即可。

代码展示：

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n,1), count(n,1);//统计每次的每次的最终结果int retlen = 1, retcount = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){//当出现递增的时候if (nums[j] < nums[i]){//判断如果加上递增的那一个和当前最长的长度还是一样的则需要更新countif (len[j] + 1 == len[i])count[i] += count[j];//如果加上当前的一个元素比比之前的最长的子序列要长，则重新规划长度else if (len[j] + 1 > len[i])count[i] = count[j],len[i] = len[j];}}//统计每次的结果，如果len和结果的len相同，则直接用count累加if (retlen == len[i])retcount += count[i];//如果len比结果的len要大，则直接重置结果len和结果的countelse if (retlen < len[i])retcount = count[i], retlen = len[i];}return retcount;}
};

运行结果：
在这里插入图片描述

4.最长数对链

题目链接
题目：

样例输出和输入：

这道题其实和求最长子序列的长度是相同的题，但是换了一个形式而已，根据题目条件我们可以得知什么是数对链：
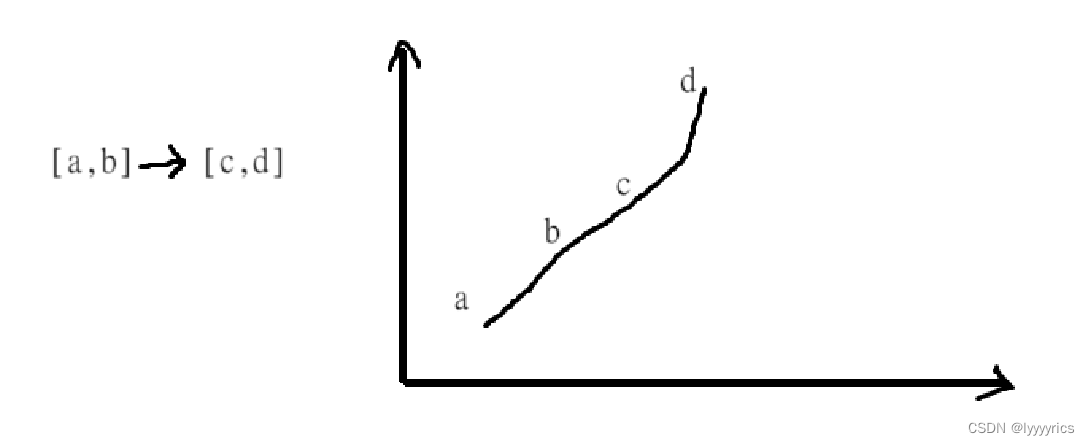
在这里插入图片描述
数对连就要满足上述条件
算法原理：
预处理：首先我们得将数组排序，排序的规则，只需要比较每个数对的第一个元素的大小即可，因为每个数对都是单增的，如果我们排序之后保证了a>c，那么d>c是绝对大于前一个数对的，所以这里只需要根据前一个数排序即可。
状态表示：这里dp[i]表示以i位置为结尾的所有数对链中最长的那个数对链的长度。
状态转移方程：分两种情况：
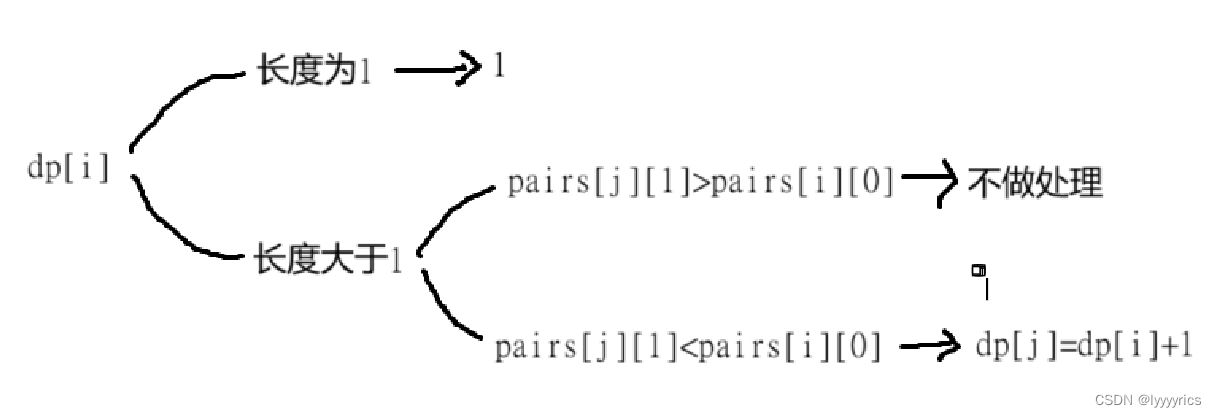
在这里插入图片描述

代码展示：

class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (pairs[j][1] < pairs[i][0]){dp[i] = max(dp[j] + 1, dp[i]);}ret = max(dp[i], ret);}}return ret;}
};

运行结果：
在这里插入图片描述

5.最长定差子序列

题目链接
题目：

样例输出和输入：

这道题给定一个difference，让我们求出数组中的差为difference的最长的子序列的长度
算法原理：
状态表示：dp[i]表示以i位置为结尾的所有子序列中的最长的等差子序列，且差值是difference。
状态转移方程：首先我们可以分析一下，我们可以选择从0位置开始遍历寻找和i位置之差是difference的数，这里的dp表其实我们可以借助hash表来充当，因为每次我们都得去前面找和i位置差值是difference的数，所以这里hash表既可以充当dp表，也可以将前一个位置和当前位置的差值是difference的数存起来。
这里的状态转移方程：hash[arr[i]] = hash[arr[i] - difference] + 1这里如果没有在hash表中找到前一个位置差值是difference值的数，则hash[arr[i] - difference]就是0，所以也免去了这种情况，由于我们找的是离i位置最近的前一个位置，这里也可以用hash表解决，因为，我们是从左到右遍历的，这就使得后一个位置每次都是覆盖了前一个位置的值，每次都是最新的状态值。

代码展示：

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;//arr[i]----dp[i]hash[arr[0]] = 1;int ret = 1;for (int i = 1;i < arr.size();i++){//需要的最后一个b的值，这个hash能保证，因为从左到右遍历，前面的值已经被覆盖了hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};