笔者近期上了国科大周晓飞老师《强化学习及其应用》课程,计划整理一个强化学习系列笔记。笔记中所引用的内容部分出自周老师的课程PPT。笔记中如有不到之处,敬请批评指正。
文章目录
- 1.1 概述
- 1.2 Markov决策过程
- 1.2.1 Markov Process (MP) 马尔科夫过程
- 1.2.2 Markov Reward Process (MRP) 马尔科夫回报过程
- 1.2.3 Markov Decision Process (MDP) 马尔科夫决策过程
- 1.3 强化学习
1.1 概述
强化学习:通过与环境互动,获取环境反馈的样本;回报(作为监督),进行最优决策的机器学习。
强化学习的过程可以用下图进行描述:在状态S1下选择动作a1,获取回报R1的同时跳转到状态S2;在状态S2下选择动作a2,获取回报R2的同时跳转到状态S3……如此循环下去。
强化学习的目标就是:对于给定的状态S,我们能选一个比较好的动作a,使得回报最大。

1.2 Markov决策过程
1.2.1 Markov Process (MP) 马尔科夫过程
一个马尔科夫过程是一个元组<S,P>,其中S表示一个有限的状态集合,P表示一个状态转移矩阵。
比如:下图矩阵P中的P1n表示,t时刻状态为n的情况下,t+1时刻转移到状态1的概率。矩阵P中的第一行表示从状态1转移出去的概率,最后一行表示从状态n转移出去的概率,所以矩阵中每一行的和都是1。

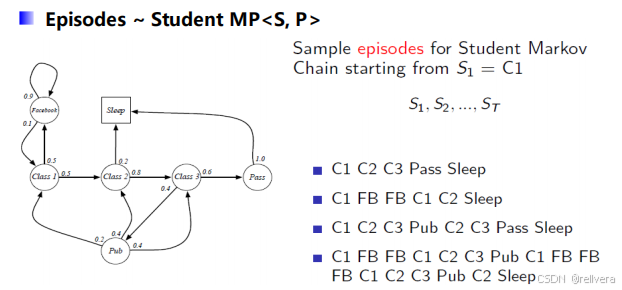
这是Markov过程的一个例子:
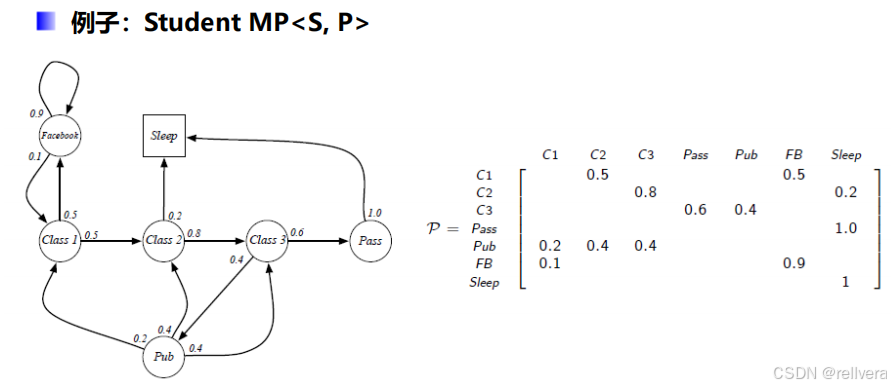
在这个例子中,假设初始状态为C1(即class1),进行4次采样,可以得到4个采样结果:
1.2.2 Markov Reward Process (MRP) 马尔科夫回报过程
马尔科夫回报过程也是一个元组 < S , P , R , γ > <S,P,R,\gamma> <S,P,R,γ>,相比于马尔科夫过程MP,MRP多了 R R R和 γ \gamma γ。其中, R R R表示在给定状态 s s s的情况下,未来回报的期望。 γ \gamma γ则是折扣因子。

那么,该怎么计算回报呢?假设当前时间为 t t t,要计算从时间 t t t开始获得的奖励 G t G_t Gt。最直接的方法是计算 G t = R t + 1 + R t + 2 + R t + 3 . . . . . . G_t=R_{t+1}+R_{t+2}+R_{t+3}...... Gt=Rt+1+Rt+2+Rt+3......,但是这样计算是不好的。
第一,如果这么算,就认为未来的奖励和当前的奖励同等重要,这在许多现实问题中并不合理。例如,在金融和经济领域,时间越长的不确定性越高,因此更倾向于重视当前的收益。
第二,在无限时间步长的过程中,累积奖励的和可能是发散的,这会导致价值函数无法计算和优化。
所以,引入了折扣因子 γ \gamma γ。奖励计算方法如下图公式所示。 γ \gamma γ趋向于0时,表示更注重当前奖励, γ \gamma γ趋向于1时,表示更具有远见。

下面是一个MRP的计算实例。首先进行采样得到几个观测序列。然后套上面的公式得到观测序列的回报,初始状态为 C 1 C1 C1, γ \gamma γ取值为1/2(每一个动作对应的回报值在下一张图片上有)。

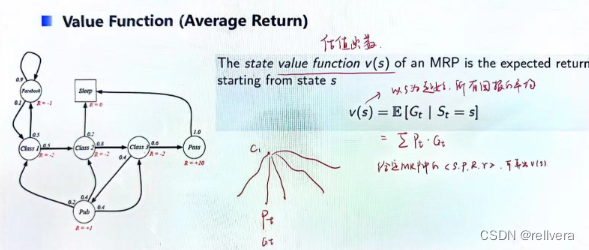
在MRP中还有一个要提的概念是估值函数(value function),它表示以状态s为起始,所有回报的平均。就像下图中所画的一样,假设从状态c1起始进行采样,得到多个观测序列,每一个观测序列都有对应被采样到的概率 P t P_t Pt,以及获得的回报 G t G_t Gt。将 P t ∗ G t P_t*G_t Pt∗Gt再求和就是估值函数v(s)。
所以,当MRP确定的时候,v(s)就是确定的值。
那么v(s)该如何计算呢?
Bellman方程将这个估值函数表示为即时奖励和后续状态价值的和,其公式如下图所示。

然后可以通过解方程解求出v(s),如下图所示。下图中的 R R R、 g a m m a gamma gamma、 P P P都是MRP中的已知量,只有v(1)~v(n)是未知量。也就是说,当 MRP(环境参数)已知时,理论上通过求解 Bellman 方程式可以计算 v(s)。
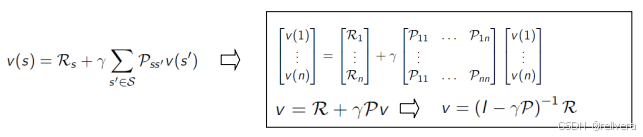
1.2.3 Markov Decision Process (MDP) 马尔科夫决策过程
MDP的定义:相比于MRP,MDP多了一个有限的动作集A。可以理解为:MDP 是一个多层的 MRP,每一层对应一个行动 a。

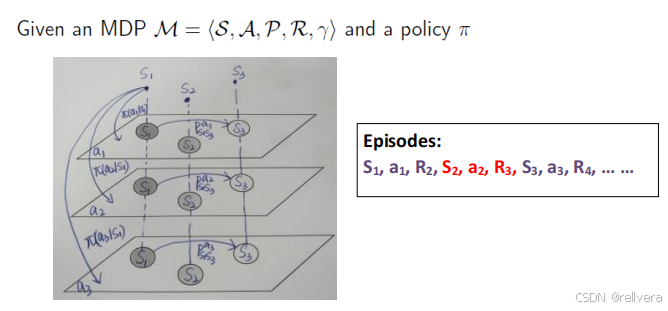
那么给定一个状态s,我们该选择怎样的行动a呢?这就要提到策略 π π π(policy π π π)了,策略 π π π表示在状态s情况下,跳转到动作a的概率。

这是一个MDP示意图。图中每一层代表了一个MRP,也隐含了一个动作a。选择a的过程其实就是在不同层之间跳转。
通过推导可以得出下面两个结论:
(1)MDP by a policy is a MP
这意味着,一旦我们固定了策略 𝜋,在任意状态 𝑠下采取动作 𝑎 的概率就确定了,这样原来的MDP就变成了一个不再依赖动作选择的过程,即一个Markov Process (MP)。
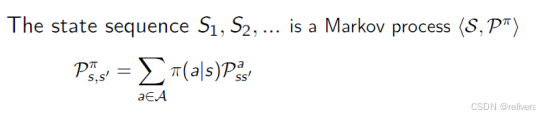
(2)MDP by a policy is also a MRP
这意味着,在有了策略 𝜋 后,MDP中的奖励也可以固定下来,即从状态 𝑠 到状态 𝑠′ 的转移的期望奖励。

再补充几个概念:
(1)state-value function v π ( s ) v_π(s) vπ(s):从状态s开始,按照策略 π π π进行决策得到的期望回报
(2)action-value function q π ( s , a ) q_π(s,a) qπ(s,a):从状态s开始,采取动作a,按照策略 π π π进行决策得到的期望回报
(3) v π ( s ) v_π(s) vπ(s)和 q π ( s , a ) q_π(s,a) qπ(s,a)的关系如下图中红色方框中的公式所示。

此时,有了MDP by a policy is a MP、MDP by a policy is also a MRP这两个结论后,我们可以进一步推导出:

从而得到贝尔曼期望方程:
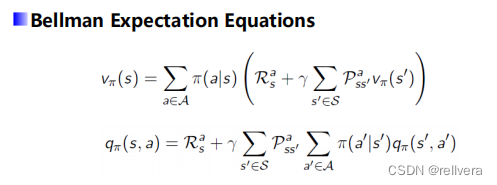
Bellman期望方程有啥用呢?
(1)策略评估。用于评估一个给定策略 𝜋 的价值函数 V π ( s ) V^π(s) Vπ(s)和 Q π ( s , a ) Q^π(s,a) Qπ(s,a)。通过迭代的方法,可以逐步逼近真实的值函数。
(2)策略改进。在策略迭代和值迭代算法中,Bellman期望方程用于评估当前策略,并根据评估结果改进策略,从而逐步找到最优策略。
1.3 强化学习
再回想一下强化学习的目标,在强化学习中,我们的目标是对于给定的状态S,我们能选一个比较好的动作a,使得回报最大。即:学习一个策略 π π π,让 v π ( s ) v_π(s) vπ(s)和 q π ( s , a ) q_π(s,a) qπ(s,a)最大。为了达到这个目标,引入了optimal state-value function v π ( s ) v_π(s) vπ(s)和optimal action-value function q π ( s , a ) q_π(s,a) qπ(s,a):

在此基础上推导出了贝尔曼最优方程:

推导过程详见这篇博文:贝尔曼最优方程推导,这篇文章写得挺好的,所以笔者在此就不多赘述啦,大家直接看这篇文章就好!
贝尔曼最优方程定义了最优值函数和最优动作值函数。最优值函数表示从状态 𝑠 出发,按照最优策略所能获得的最大期望回报。最优动作值函数表示在状态 𝑠 采取动作 𝑎 后,按照最优策略所能获得的最大期望回报。
贝尔曼最优方程在强化学习中可以用来定义和求解最优策略,使得在每个状态下的累积回报最大化。它为我们提供了一种系统的方法,通过动态规划和迭代更新来逼近最优解,是解决强化学习问题的核心工具。




![[译]Reactjs性能篇](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Ffacebook.github.io%2Freact%2Fimg%2Fdocs%2Fshould-component-update.png&pos_id=img-oQfScO9b-1720015041810)