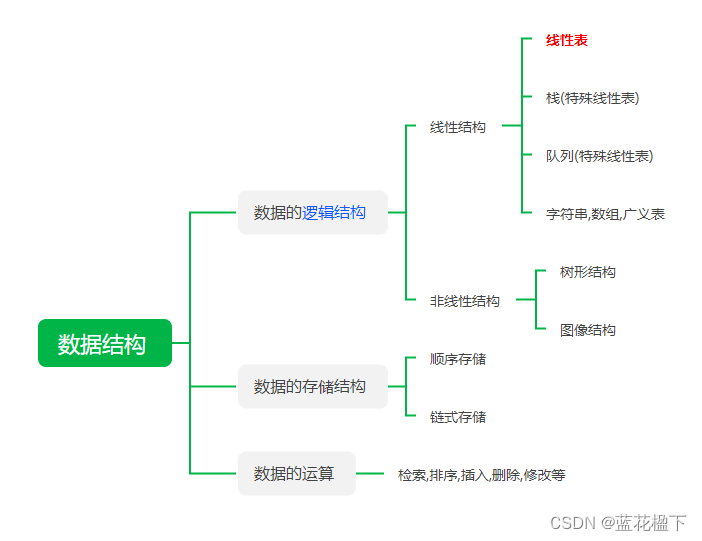
线性表的定义和特点
线性表是具有相同特性的数据元素的一个有限序列
:线性起点/起始节点
:
的直接前驱
:
的直接后继
:线性终点/终端节点
n:元素总个数,表长
下标:是元素的序号,表示元素在表中的位置
n=0时称为空表
线性表
由n(n>0)个数据元素(结点),组成的有限序列
将非空的线性表(n>0)记作:()
这里的数据元素(
)只是一个抽象的符号,其具体含义在不同的情况下,可以不同
例1
分析26个英文字母组成的英文表
(A,B,C...Z)
数据元素都是字母,元素间关系是线性关系
例2
分析学生情况登记表
略
每条记录也是线性关系
例3
某单位历年拥有计算机的数量(4,6,45,34,33) 线性关系(先后)
例4
12星座 (白羊座,金牛座,...双鱼座) 线性关系(先后)
同一线性表的元素必定有相同特性,数据元素之间的关系是线性关系
综上 线性表的逻辑特征是:
在非空的线性表中,有且一个开始节点,它没有直接前趋,仅有一个后继
在非空的线性表中,有且一个终端节点,它没有直接后继,仅有一个前趋
其余节点(
) 仅有一个前趋
,仅有一个后继
线性表是一种典型的线性结构
线性表案例
例1
一元多项式的运算:实现两个多项式加,减,乘运算
线性表P=()
每一项的指数i隐含在其系数的序号中
用数组来表示
指数用下标表示,系数用具体值表示
操作
两个多项式相加
线性表R = ()
例2:稀疏多项式
如果用前面下标代表指数,会造成空间浪费
多项式非零项的数组表示
线性表
线性表A=((7,0),(3,1),(9,8).(5,17))
线性表B=((8,1),(22,7),(-9,8))
创建一个新数组c
分别从头遍历比较a和b的每一项
指数相同,对应系数相加,若其和不为0,则在c中加一个新项
指数不相同,则将指数较少的项复制到c中
一个多项式遍历完毕时,将另一个剩余项依次复制到c即可
缺陷:并不知道数组c的空间要分配多少
顺序存储结构存在问题
存储空间分配不灵活
运算的空间复杂度高(需要额外的空间)
解决问题
链式存储结构 后续详细介绍
例3:图书信息管理系统
需要的功能: 增(插入)删改查排序计数
图书表抽象为线性表
表中每本书抽象成线性表中的数据元素
图书顺序表:数组存储
图书链表:链表存储
选择适当的存储结构
实现此存储结构上的基本操作
利用基本操作完成功能
总结:
线性表中数据元素的类型可以为简单类型,也可以为复杂类型
许多实际应用问题所涉及的基本操作有很大相似性,不应为每个具体应用单独编写一个程序
从具体应用中抽象出共性的逻辑结构和基本操作(抽象数据类型),然后实现其存储结构和基本操作
线性表的类型定义
抽象数据类型线性表的定义如下:
ADT List{
数据对象: D = { 属于Elemset,
}
数据关系: R = { 属于
(i=2,3,....n)}
基本操作:
InitList(&L)
略
} ADT List
基本操作:
初始化线性表
InitList(&L)
操作结构:构造一个空的线性表L
销毁线性表
DestroyList(&L)
初始条件:线性表L已经存在
操作结果:销毁线性表L
清除线性表
ClearList(&L)
初始条件:线性表L已经存在.
操作结果:将线性表L重置为空表
判断线性表是否为空
ListEmpty(L)
初始条件:线性表L已经存在
操作结果:若线性表L为空表,则返回Ture,否则返回False
返回线性表L的元素个数
ListLlenth(L)
初始条件:线性表L已经存在
操作结果:返回线性表L中的数据元素个数
返回线性表第i个元素的值
GetElem(L,i,&e);
初始条件:线性表L已经存在,1<=i <= ListLenth(L)
操作结果:用e 返回线性表L中第i个元素的值
返回L中第1个与e满足compare()的数据元素的位序
LocateElem(L,e,compare())
初始条件:线性表L已经存在,compare()是数据元素判定函数
操作结果:返回L中第1个与e满足compare()的数据元素的位序,若这样的数据元素不存在则返回值为0.
待补充
忘保存,明天补上
线性表的顺序表示和实现2

顺序表的特点:
以物理位置相邻表示逻辑关系
任一元素均可随机存取(优点)
用高级语言实现数据类型

用一维数组表示顺序表
线性表可变(删除)
数组长度不可动态定义
注:一维数组的定义方式
类型说明符 数组名[常量表达式]
说明:常量表达式中可以包含常量和符号常量,不能包含变量,, 即C语言中不允许对数组的大小做动态定义
解决方式:用一变量表示顺序表的长度属性
如下所示
c定义结构体
#define LIST_INIT_SIZE 100
//线性表存储空间的初始分配量
//定义了一个结构体 SqList,包含一个数组和一个整型变量
typedef struct { Elem Type elem[LIST_INIT_SIZE];int length; //当前长度
} SqList;实例
多项式的顺序存储结构类型定义
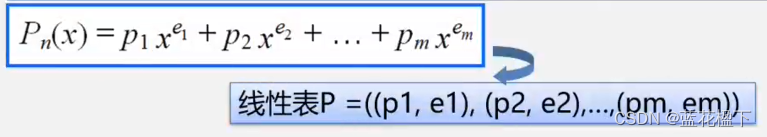
c实现
#define MAXSIZE 1000
//多项式可能达到的最大长度//结构体:多项式非零项定义
typedef struct {float p; //系数int e; //指数
} Polynomial;//结构体:多项式顺序存储结构
typedef struct{Polynomial *elem; //基地址int length; //当前项个数
} SqList;图书表的顺序存储结构类型定义
#define MAXSIZE 10000
//图书表可能达到的最大长度//图书信息定义
typedef struct {char no[20]; //图书ISBNchar name[50]; //图书名字float price; //图书价格
} Book;//图书表顺序存储结构类型为SqList
typedef struct {Book *elem; //存储空间的基地址int length; //图书表中当前图书个数
}SqList; //图书表的顺序存储结构类型为SqList补充知识:
元素类型说明
顺序表类型定义
类c
typedef struct {ElemType data[]; //ElemType一般是自定义的顺序表里的元素类型int length;
} SqList; //顺序表类型ElemType一般是自定义的顺序表里的元素类型
如下所示
typedef strcut {float p;int e;
} Polynomial;typedef strcut {Polynomial *elem;int length;
}SqList;数组定义
静态分配
typedef struct {ElemType data[MaxSize];int length;
} SqList; 动态分配
typedef struct{ElemType *data;int length;
}SqList;动态分配创建变量
#include <stdlib.h>
typedef struct{ElemType *data;int length;
}SqList;SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)*MaxSize);
//MaxSize:数组最大长度 sizeof:获取类型长度 malloc分配固定长度的空间
//释放指针p所指变量的存储空间,即彻底删除一个变量
free(L.data)c++动态存储分配
new 类型名(初值列表)
功能:申请用于存放T类型对象的内存空间,并根据初值列表赋初值
结果值;
成功:T类型的指针,指向新分配的内存
失败:0
int *p1 = new int;
int *p2 = new int(10);
delete p1;