题目如下,其中周期是 2 π 2\pi 2π
y = { 1 0 < x < π 0 x = 0 − 1 − π < x < 0 y=\begin{cases} 1 \ 0<x<\pi\\ 0 \ x=0\\ -1 \ -\pi <x<0\\ \end{cases} y=⎩ ⎨ ⎧1 0<x<π0 x=0−1 −π<x<0
计算可得
a n = 1 π ∫ − π π y ( x ) cos ( n x ) d x = 0 (由于是奇函数乘偶函数) a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} y(x) \cos(nx) \, dx=0 (由于是奇函数乘偶函数) an=π1∫−ππy(x)cos(nx)dx=0(由于是奇函数乘偶函数)
b n = 1 π ∫ − π π y ( x ) sin ( n x ) d x = 1 π ( ∫ − π 0 ( − 1 ) sin ( n x ) d x + ∫ 0 π 1 ⋅ sin ( n x ) d x ) = 2 ( 1 − ( − 1 ) n ) π n b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} y(x) \sin(nx) \, dx \\ = \frac{1}{\pi} \left( \int_{-\pi}^{0} (-1) \sin(nx) \, dx + \int_{0}^{\pi} 1 \cdot \sin(nx) \, dx \right) =\frac{2(1-(-1)^n)}{\pi n} bn=π1∫−ππy(x)sin(nx)dx=π1(∫−π0(−1)sin(nx)dx+∫0π1⋅sin(nx)dx)=πn2(1−(−1)n)
因此,该函数的傅里叶级数表示为:
y ( x ) = ∑ n = 1 ∞ 4 π ( 2 n − 1 ) sin ( ( 2 n − 1 ) x ) ( − π < x < π ) y(x) = \sum_{n=1}^{\infty} \frac{4}{\pi (2n-1)} \sin((2n-1)x) \quad (-\pi < x < \pi) y(x)=n=1∑∞π(2n−1)4sin((2n−1)x)(−π<x<π)
代码如下
k=30;%用k代替无穷大,k越大,越接近
t=-pi:pi/200:pi;%代表x
y=0;
for i=1:2:k %奇数个才不为0y=y+4*sin(i*t)/(i*pi);
end
plot(t,y);
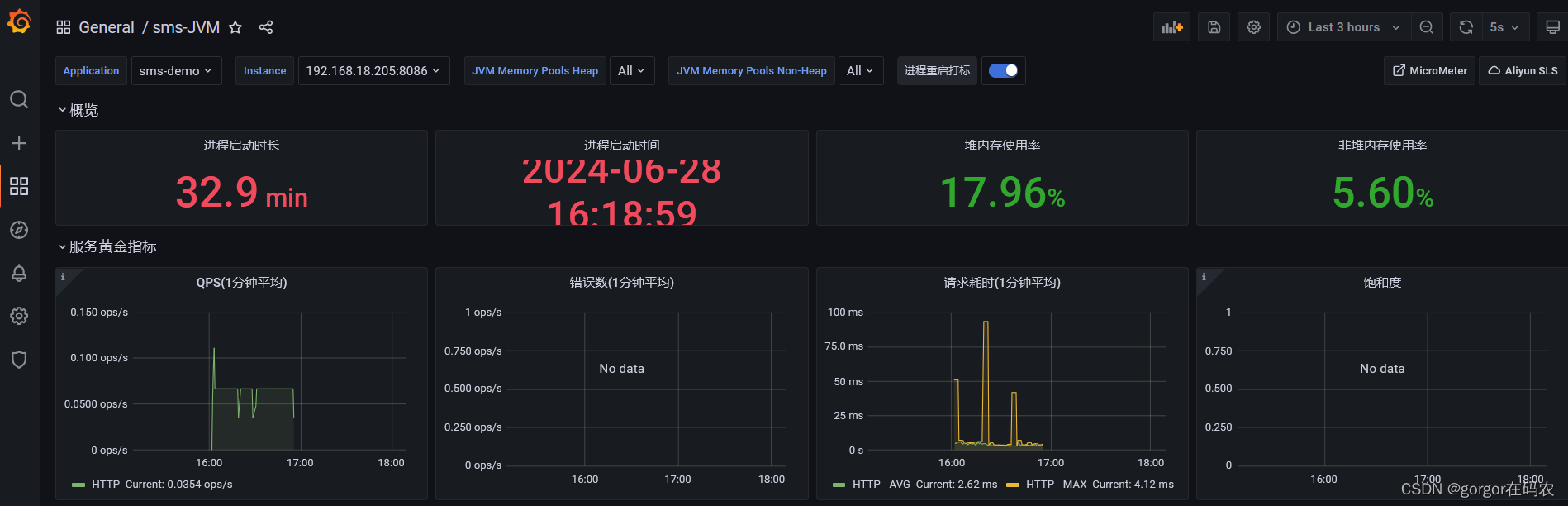
效果如图