Studying-代码随想录训练营day27| 贪心算法理论基础、455.分发饼干、376.摆动序列、53.最大子序和

第27天，贪心开始！(ง •_•)ง💪，编程语言：C++

贪心算法理论基础

贪心的套路

贪心的一般解题步骤

总结

455.分发饼干

376.摆动序列

53.最大子序和

总结

贪心算法理论基础

什么是贪心？—— 贪心的本质是选择每一个阶段的局部最优，从而达到全局最优。例如：你可以拿走十张，如果想达到最大的金额，你要怎么拿？指定每次拿最大的，最终结果就是拿走最大数额的钱！

但要注意的是只有局部最优能够推出全局最优，也就是没有反例的情况下，才能够使用贪心算法。因为比如说再举一个例子如果是有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，就不行了，需要考虑了的条件增加了许多，这时候就需要动态规划，而不是贪心了。

贪心的套路

总结：贪心算法没有固定套路。说到底贪心只有一句话通过局部最优，推出整体最优，而能否从局部最优推出整体最优，只能通过思考，模拟，并且举反例的方式来确定。一般来说最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。

对于贪心来说最重要的是能够想到模拟策略，面试中最重要的也是能够自圆其说即可。刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

贪心算法很多情况下都是常识性推导，让人认为本应该就这么做，这也是贪心难的地方，能够想到就能解出，但如果想不到就很难解出了。

贪心的一般解题步骤

贪心算法一般分为四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

但事实上以上四步有些过于理想化，我们做题的时候不会说按照这样去思考，因此最重要的还是想清楚局部最优是什么，并且如何推导出全局最优。

总结

贪心算法没有套路，有的只是常识性的推导和灵感的碰撞。

455.分发饼干

文档讲解：代码随想录分发饼干

视频讲解：手撕分发饼干

题目：

学习：本题算是比较经典的贪心算法之一。首先需要理解题干的意思：有一堆饼干和一群小孩，把饼干分给小孩，但每个小孩只能分得一块饼干。每块饼干具有一个尺寸值，每位小孩具有一个胃口值，只有当尺寸值大于胃口值时，小孩才能够满足。

给予以上分析，可以推出局部最优就是尽可能大尺寸的饼干满足大胃口的人（牢记一块饼干只能给一个人），从而得到总体最优满足最多的人。

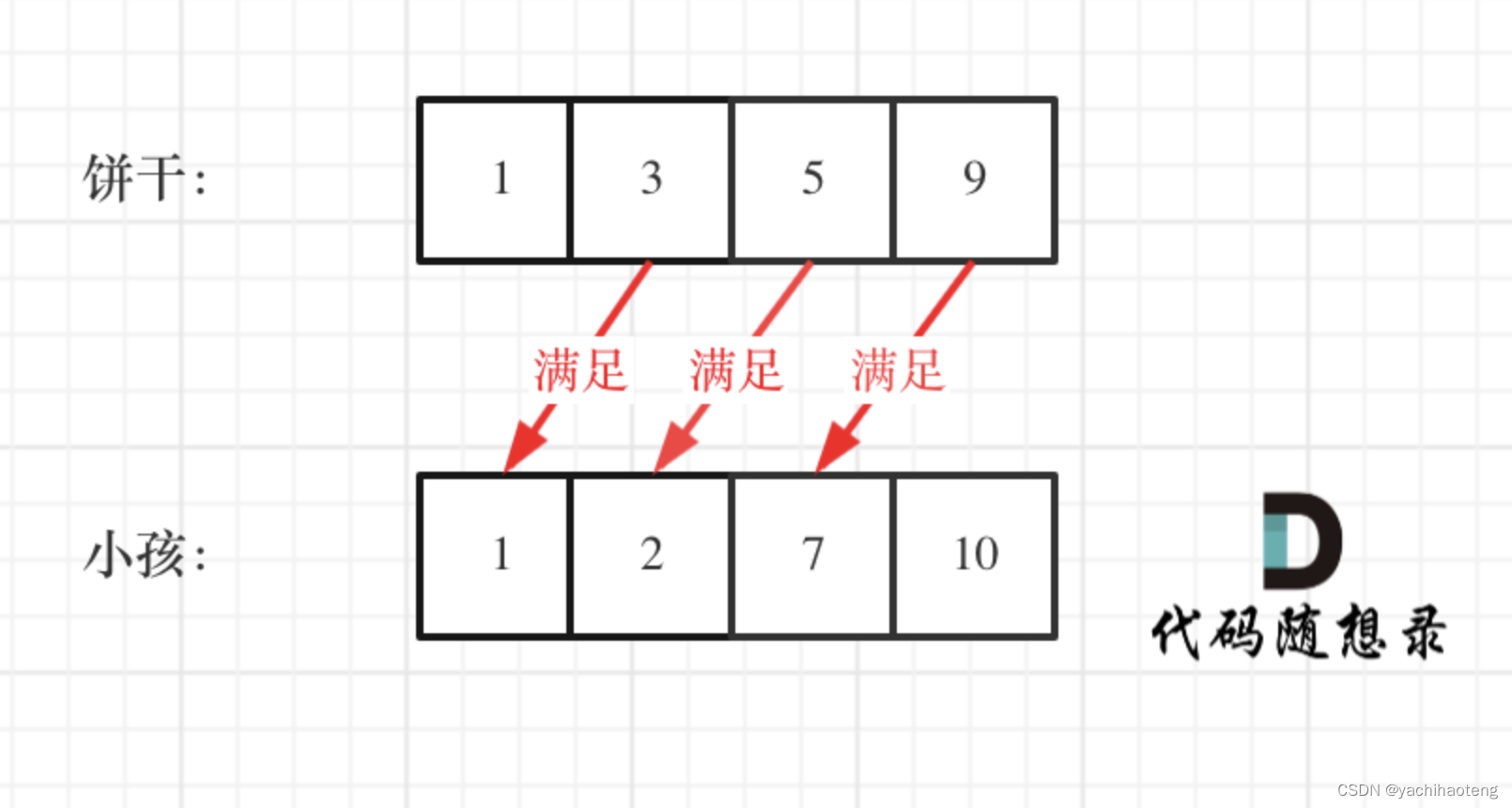
根据上述策略，我们首先要对饼干和小孩两个数组进行排序，而后选择尺寸最大的饼干，之后遍历小孩找到符合要求的最大胃口的小孩，接着在选择下一块饼干继续遍历（要注意遍历小孩我们也是从胃口最大的开始遍历，因此选择下一个饼干时我们不需要从头遍历，因为胃口大的那些小孩肯定不会满足尺寸更小的饼干，继续遍历就可以了）

代码：

//时间复杂度O(nlogn + mlogm)两个排序的时间复杂度
//空间复杂度O(1)
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int count = 0; //记录小孩数量//先进行排序sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1; //指向最后一个元素，此时为最大饼干for(int i = g.size() - 1; i >= 0 && index >= 0; i--) {if(g[i] <= s[index]) {count++;index--;}}return count;}
};

本题还可以采取小饼干先喂小胃口的人的方法，但此时要注意先选择小胃口的人，然后遍历饼干，因为此时我们需要的是找到满足最小胃口的最小饼干，和前面的找到满足最大饼干的最大胃口是相反的。

代码：

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {//第二种方法，先遍历胃口再遍历饼干（先满足小胃口的）sort(g.begin(), g.end());sort(s.begin(), s.end());int index = 0;//遍历饼干，找到符合最小胃口的小孩for(int i = 0; i < s.size() && index < g.size(); i++) {if(s[i] >= g[index]) {index++; //查找下一个胃口小的小孩}}return index; //满足了多少个小孩，就是答案数量}
};

376.摆动序列

文档讲解：代码随想录摆动序列

视频讲解：手撕摆动序列

题目：

学习：本题理解题意，摆动序列指的是数字之间的差是正负数摇摆交替的，可以通过删除一些元素，来使得剩余元素组成的序列是摇摆序列。如果仅有一个元素或者含两个不等元素的序列也视作摇摆序列。

首先我们很容易能够想到，找到波峰和波谷，删除中间多余的元素，就能够组成一个摇摆序列。

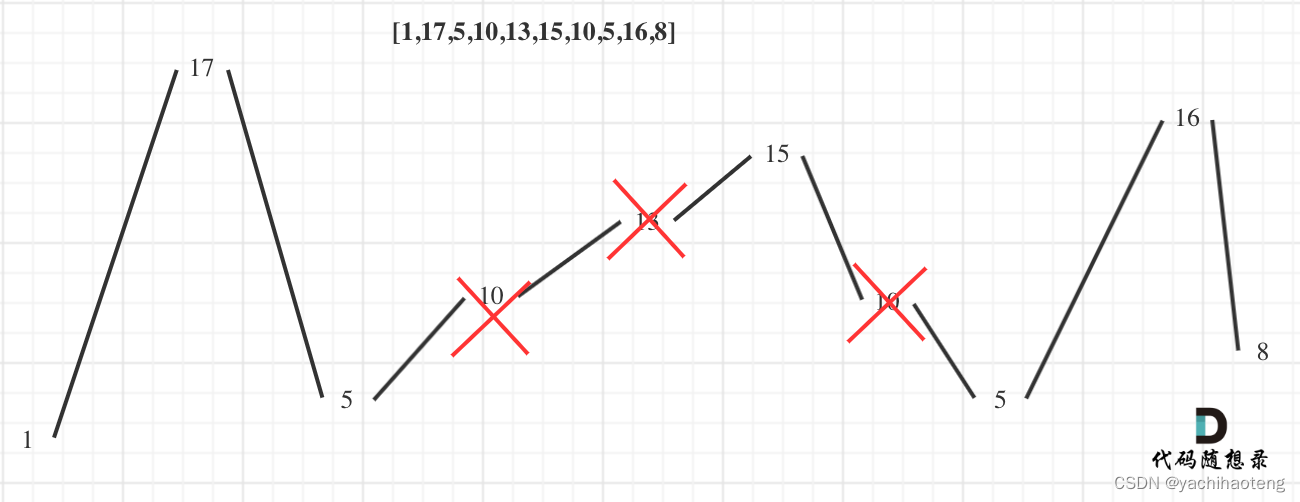
在解题过程中，我们不需要删除多余的元素，只需要保存波峰和波谷的元素就能够得到元素最多的摆动序列，并且本题甚至只需要返回长度值，不需要我们把元素进行保存。

但本题不能仅仅判断左右差值是否为正负，我们需要考虑除上图情况以外的三种情况：

情况一：上下坡中有平坡

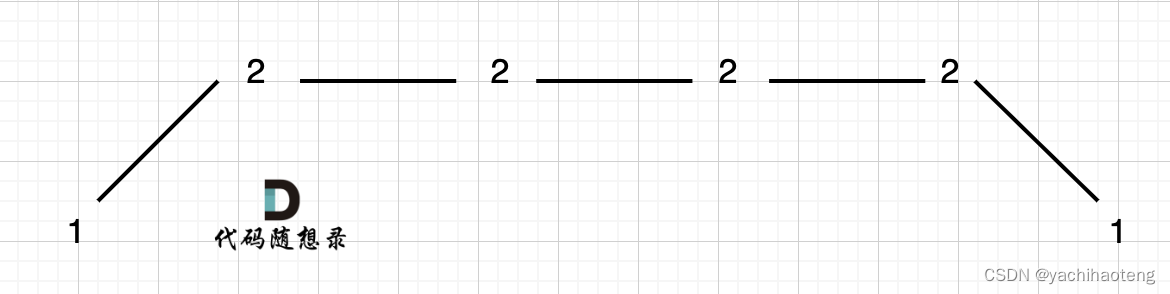
对于这种情况，显然是把中间多余的三个3去除，最后留下（1，2，1）序列，也就是长度为3。但本题2在的位置不是明显的波峰或是波谷，不能通过判断左右差值为正负来进行。因此我们需要单独考虑该情况的逻辑。

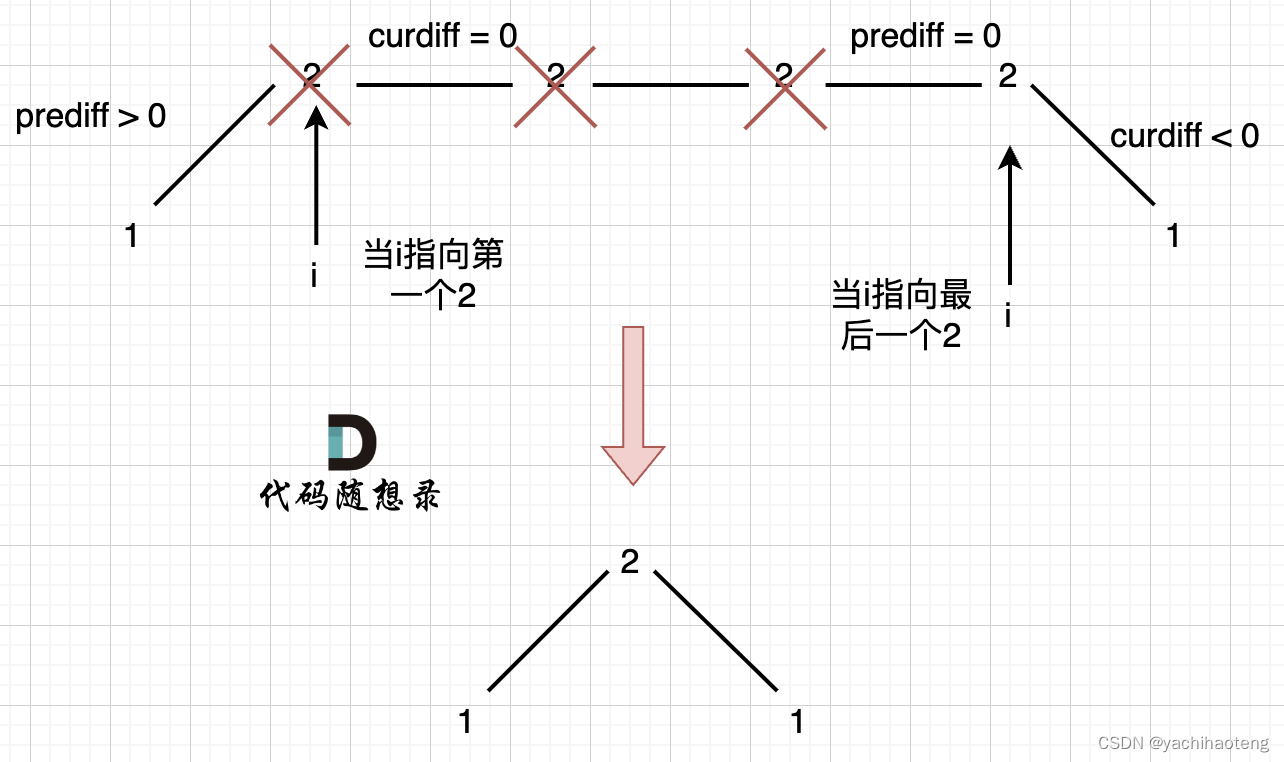
当i指向第一个2的时候，prediff > 0 & curdiff = 0，当i指向最后一个2的时候，prediff = 0 && curdiff < 0。这两个条件都可以，但是为了便于我们进行从左到右的遍历，我们这边采用删除左面三个2的规则，因此当prediff = 0 && curdiff < 0时要记录一个峰值，这是上坡的情况。下坡的情况就是prediff = 0 && curdiff > 0的情况也要记录一个峰值。加上前面的判断正负的情况，因此我们要记录峰值的条件应该是：(prediff <= 0 && curdiff > 0) || (prediff >= 0 && curdiff < 0)。

情况二：数组首尾两端

因为本题的要求，如果只有一个元素则摆动序列为1，如果有两个元素且两个元素不同的情况下摆动序列为2。但我们在计算prediff和curdiff的时候，至少需要三个数字才能进行计算。我们可以通过单独列出一个if 来处理当元素只有两个的情况。但我们也可以将其加入到统一的循环当中，那就是让prediff初始 = 0。例如我们针对序列[2,5]，可以假设为[2,2,5]，这样也就有了坡度。

针对上述情形，我们的result初始为1，默认最右面有一个数值（符合我们上面说的遍历规则）。当出现上述情况的时候，result就会+1，最后得到的就是2。这样也能够处理超过两个数并且所有数都是一样的情况。

情况三：单调坡度有平坡

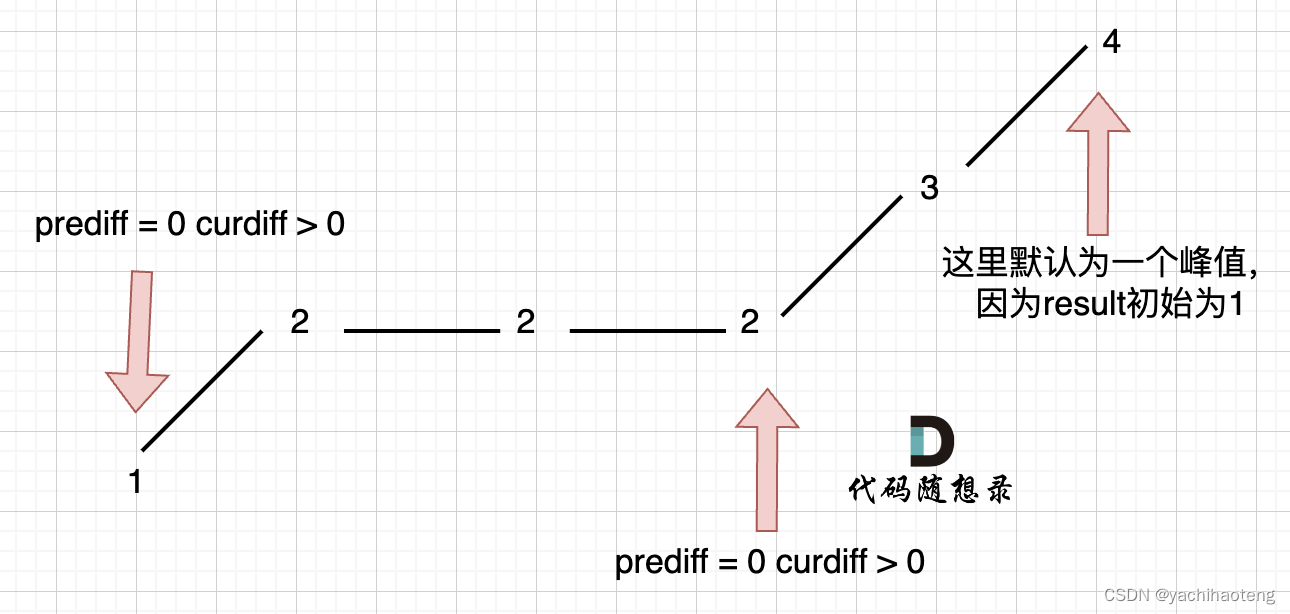
可以看出针对这种情况，我们在情况一中使用的方法可能就会带来错误，因为上述的序列，我们最后得到的只能是[1,4]或者时其他长度为2的摆动序列。因此我们这边要注意的是prediff的更新逻辑。prediff不能实时进行更新，它保存的不仅仅是差值还应是数组的一个趋势，因此prediff应该在有坡度摆动变化的时候进行更新，也就是出现峰值的时候我们再进行更新。

代码：解决上述三种情况后，可以得到代码：

//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() == 1) return 1; //如果只有一个元素，返回1int prediff = 0; //前端差值int curdiff = 0; //后段差值int result = 1; //记录结果，默认加入尾元素，首元素单独处理，防止出现所有元素都相同的情况//不遍历尾元素for (int i = 0; i < nums.size() - 1; i++) {curdiff = nums[i + 1] - nums[i];//出现峰值if((prediff >= 0 && curdiff < 0) || (prediff <= 0 && curdiff > 0)) {result++;prediff = curdiff; //当需要记录结果的时候，再改变前端差值，保证当前数组趋势}}return result;}
};

53.最大子序和

文档讲解：代码随想录最大子序和

视频讲解：手撕最大子序和

题目：

学习：本题显然可以通过两个for循环进行暴力求解。但本题同样也可以使用贪心算法来降低时间复杂度。本题的贪心逻辑在于我们从头开始遍历的过程中，如果发现加和为负数，就立马抛弃目前的“连续和”，因为负数参与加和只会使得数变小，而不会变大。因此我们需要立马抛弃该和，从下一个元素重新计算“连续和”，由这种局部最优的方式来推导出全局最优。

注意：我们是在加和为负数的情况下，才去抛弃“连续和”，而不是遇到负数就抛弃，两者是有区别的，因为加和还不为负数时，仍然是可以给后面的数提供加大的可能性的。但我们也要通过设置一个maxcount实时记录当前count的最大值，这样也能够避免我们因为存在负数而错过最大值的情况。

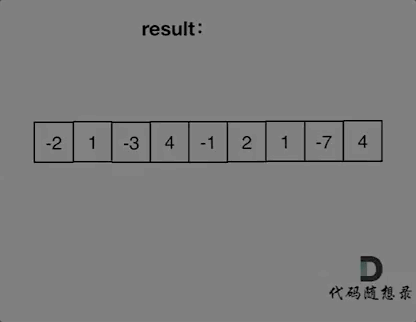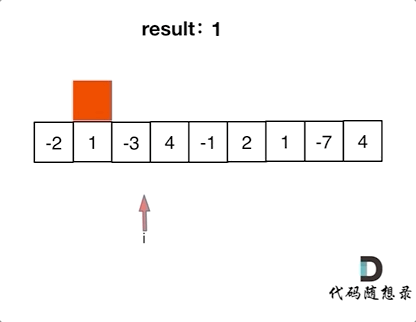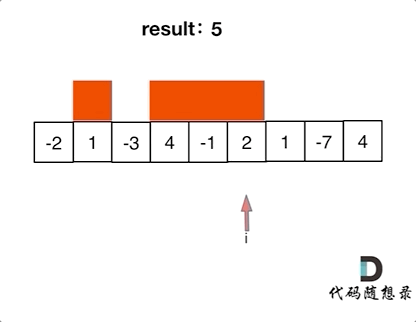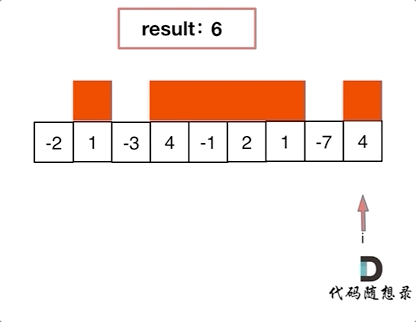
因为本题不需要我们记录最大序列的左右下标，因此本题设置一个result或者maxcount记录最大值就可以了，否则还需要设置两个左右端点来记录下标。

代码：

//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:int maxSubArray(vector<int>& nums) {int count = 0; //记录当前和int maxcount = INT_MIN; //记录最大值for(int i = 0; i < nums.size(); i++) {//如果当前和小于0，抛弃前和，改为当前值if(count < 0) {count = nums[i];}else {count += nums[i];}//如果当前和大于最大值，更新最大值if (count > maxcount) {maxcount = count;}}return maxcount;}
};