目录
- 一、数组
- 1.1、一维数组
- 1.1.1 、一维数组的定义方式
- 1.1.2、一维数组的数组名
- 1.2、二维数组
- 1.2.1、二维数组的定义方式
- 1.2.2、二维数组的数组名
- 二、对称矩阵的压缩存储
- 三、三角矩阵的压缩存储
- 四、三对角矩阵的压缩存储
- 五、稀疏矩阵的压缩存储
一、数组
概述:数组是一个集合,用于存放相同数据类型的元素
1. 特点一: 数组中的每个数据元素具有相同的数据类型;
2. 特点二: 数据占用一段连续的内存空间
1.1、一维数组
1.1.1 、一维数组的定义方式
- 只能用数字,字母和下划线命名,且不能用数字作为开头,注意数组名不要与其他变量名重复;
- 数组的下标从0开始。
一维数组的三种定义方式:
第一种:
//数据类型 数组名[数组长度];
int main(){int arr[10];//定义一个长度为10的数组,数组元素为int型//使用数组下标对数组元素进行访问arr[0] = 10;//数组第一个元素的下标为0arr[2] = 20;arr[9] = 20;//数组最后一个元素的下标为9,对于长度为i的数组,最后一位元素的下标即为i-1
}
注意:定义数组时,若未给定数组元素的初始值,则必须指定数组的长度,否则提示错误,因为编译时需要分配空间,数组长度未知的话,无法进行分配。
第二种:
//数据类型 数组名[数组长度] = {值1, 值2,...};
int main(){int arr[10] = {1, 2, 3, 4};//未设定初始值的后6位元素默认为0
}
注意: 数组初始化时,若大括号{}内的元素个数小雨定义的数组长度,则剩余的数组元素默认为0。
第三种:
//数据类型 数组名[] = {值1, 值2, ...};
int main(){int arr[] = {1,2,3,4,5,6,7,8,9,10};//数组长度为10
}
注意: 定义数组元素时,数组可以不用指定数组长度,数组长度由所定义元素的数量决定。
1.1.2、一维数组的数组名
作用一: 统计数组所占用的内存空间、数组中单个数据元素所占用的内存空间、数组的长度,如下:
#include<iostream>
using namespace std;int main(){int arr[10];cout<<"数组arr用内存空间为"<<sizeof(arr)<<endl;//40cout<<"数组arr中单个元素占用内存空间为:"<<sizeof(arr[0])<<endl;//4cout<<"数组长度为:"<<sizeof(arr)/sizeof(arr[0])<<endl;//10return 0;
}
作用二: 获取数组在内存中的地址,如下:
int main(){int arr[10];cout<<arr<<endl;//获取数组的首地址cout<<&arr[0]<<endl;//获取数组的首地址cout<<&arr<<endl;//获取整个数组的地址return 0;
}
注意: arr/&arr[0]和&arr虽然数值相同,但是含义不同!&数组名表示指针,对程序做出如下变化:
#include<iostream>using namespace std;int main() {int arr[10];cout << "数组长度为:" << sizeof(arr) << endl;cout << "" << sizeof(arr[0])<< endl;cout << "首地址为:"<<arr<<endl;cout << "地址为:" << arr+1<< endl;//与之前相差4cout << "首地址为:" << &arr[0] << endl;cout << "数组地址为:" << &arr << endl;cout << "地址为:" << &arr +1<< endl;//与之前相差了40return 0;
}
运行结果为:

注意:
- 数组名是常量,不能进行赋值,否则会报错;
1.2、二维数组
1.2.1、二维数组的定义方式
二维数组有四种定义方式;
数据类型 数组名[行数][列数];数据类型 数组名[行数][列数] = {数据1, 数据2, 数据3};数据类型 数组名[行数][列数] = {{数据1, 数据2}, {数据3, 数据4},{数据5, 数据6}};数据类型 数组名[][列数] = {数据1, 数据2, 数据3, 数据4};
第3种定义方式最直观,可以提高代码的可读性;
第2种和第4种要根据二维数组的列数推断数组元素**(可以省略行数,不能省略列数)**;
定义二维数组时,若已经初始化数据,可以省略行数。
示例如下:
#include<iostream>using namespace std;int main() {int arr[][2] = { {1,2},{4,5} };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {for (int j = 0; j < sizeof(arr[i]) / sizeof(arr[i][0]);j++) {cout << arr[i][j] << "";}cout << endl;}return 0;
}
运行结果为:

注意cout时的格式!
1.2.2、二维数组的数组名
二维数组名称的作用:
1. 计算二维数组所占内存空间;
cout << "二维数组所占空间为:" <<sizeof(arr) <<endl;cout << "二维数组中第1行所占空间为:" << sizeof(arr[0]) << endl;cout << "二维数组中某个元素所占空间为:" << sizeof(arr[0][1]) << endl;
运行结果为:

2. 计算二维数组的行数和列数
求行数:sizeof(arr)/sizeof(arr[0]);//即数组元素总数/每一行的元素数
求列数:sizeof(arr[0])/sizeof(arr[0][0])
3. 获取二维数组中的相关地址
二维数组首地址:arr[0]或者&arr[0][0]
二维数组第一个元素的地址:arr[0]或&arr[0][0]
二维数组第一行的地址:arr或arr[0]或arr+0或*(arr+0)
二维数组第i行的地址:arr[i]或&arr[0]+i或*(arr+i)
二维数组第i行首元素的地址:arr[i]或arr+i或&arr[0]+i或*(arr+i)
二维数组第i行第j列元素的地址:&arr[i][j]或*(arr+i)+j
4. 通过指针解引用访问或操作某元素:*(*(arr+i)+j)
二、对称矩阵的压缩存储
对称矩阵的矩阵压缩:
若n阶方阵中任意一个元素 都有
都有 ,则称该矩阵为对称矩阵,对于对称矩阵,只须存储对角线+下三角区。若按照优先原则将各元素存入一维数组中,即
,则称该矩阵为对称矩阵,对于对称矩阵,只须存储对角线+下三角区。若按照优先原则将各元素存入一维数组中,即 存入数组
存入数组 中,那么数组
中,那么数组 共有
共有 个元素。对于k,有:
个元素。对于k,有:


三、三角矩阵的压缩存储
- 下三角矩阵:除了主对角线和下三角区,其余的元素都相同;
- 上三角矩阵:除了主对角线和上三角区,其余的元素都相同。
- 压缩存储策略:按行优先原则将主对角线+下三角区存入一维数组中,并在最后一个位置存储常量,即
 存入数组
存入数组 中,那么数组
中,那么数组 共有
共有 个元素。对于k,有:
个元素。对于k,有:


四、三对角矩阵的压缩存储
三对角矩阵:又称为带状矩阵:当 时,有
时,有 。对于三角矩阵,按行优先原则,只存储带状部分,即
。对于三角矩阵,按行优先原则,只存储带状部分,即 存入数组
存入数组 中,那么k=2ij - 3。若一直数组下标k,则
中,那么k=2ij - 3。若一直数组下标k,则

五、稀疏矩阵的压缩存储
稀疏矩阵的非零元素远远少于矩阵元素的个数,压缩存储策略:
- 三元数组<行, 列,值>
| i(行) | j(列) | v(值) |
|---|---|---|
| 1 | 3 | 4 |
| 1 | 6 | 5 |
| 2 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 5 | 6 |
| 4 | 2 | 2 |
注意:此处的行列下标从1开始。
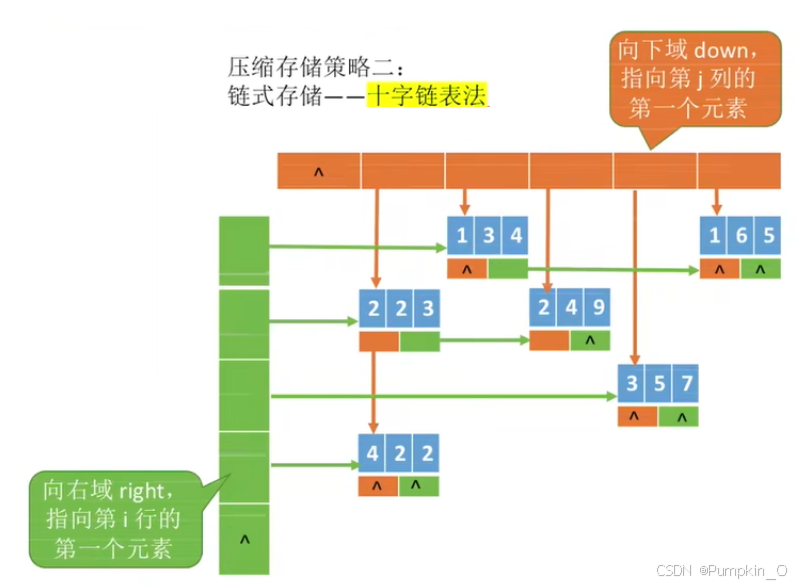
- 十字链表