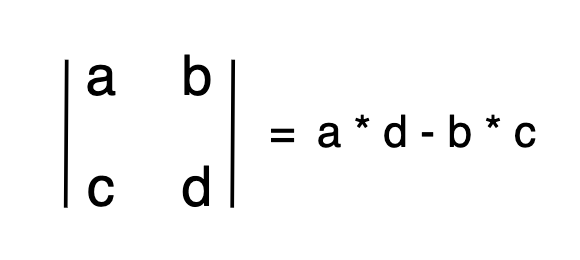常见考点1:
设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2,则n0=n2+1(叶子结点比二分支结点多一个)

常见考点2:
二叉树第一层至多右 有个结点(i>=1)
m叉树第一层至多右 有个结点(i>=1)

常见考点3:
高度为h的二叉树至多有个结点(满二叉树)
高度为h的m叉树至多有个结点
等比数列求和公式:a+aq+aq^2...+aq^n-1=
完全二叉树的常考性质
常见考点1:
具有n个(n>0)结点的完全二叉树的高度h为或
推导过程:
高度为h的满二叉数共有个结点
高度为h-1的满二叉数共有个结点
所以n个(n>0)结点的完全二叉树:
高度为h-1的满二叉数<n个(n>0)结点的完全二叉树<=高度为h的满二叉数
推导过程:
高度为h-1的满二叉数共有个结点
高度为h的完全二叉数至少有个结点,至多
个结点
得出
根据以上两种方法得出:第i个结点所在层次为或

常见考点2:
对于完全二叉树,可以由结点数n推出度为0、1和2的结点个数为n0、n1和n2
- 完全二叉树最多只有一个度为1的结点——>n1=0或1
- n0=n2+1——>n0+n2一定是奇数
由1和2可得出:
- 若完全二叉树有2k个(偶数)个结点,则必有n1=1,n0=k,n2=k-1
- 若完全二叉树有2k-1个(奇数)个结点,则必有n1=0,n0=k,n2=k-1
总结