Logistic回归模型:
适用于二分类或多分类问题,样本特征是数值型(否则需要转换为数值型)
策略:极大似然估计
算法:随机梯度 或 BFGS算法(改进的拟牛顿法)
线性回归表达式:
式子中;w为N个特征权重组成的向量,即
;b是第i个样本对应的偏置常数。
Sigmoid函数:
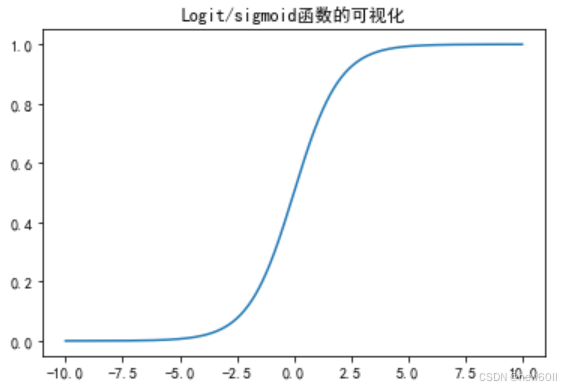
对数概率
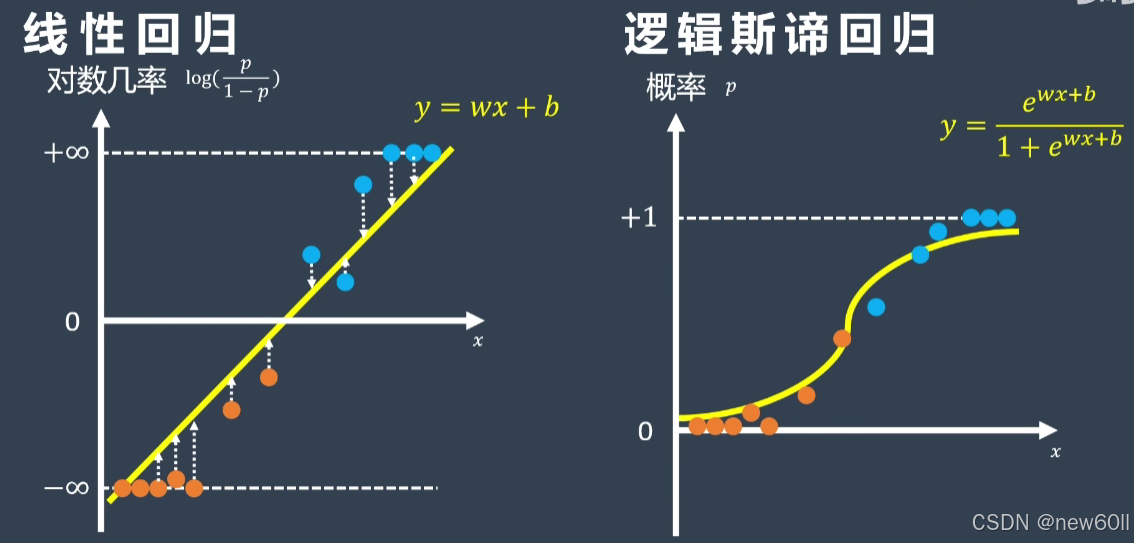
Logistic 回归模型:
,
构造似然函数:
Logistic回归优化:梯度下降,分别对权重w,偏置b求导数:
综上,可归纳Logistic回归的过程:

实例:鸢尾花数据集划分:
class Logistic_Regression:def __init__(self):self.coef_ = Noneself.intercept_ = Noneself._theta = Nonedef _sigmoid(self,t):return 1./(1.+np.exp(-t)) def fit(self,X_train,y_train,eta = 0.01, n_iters =1e4):def J(theta,X_b,y):y_hat = self._sigmoid(X_b.dot(theta))try:return -np.sum(y*np.log(y_hat) +(1-y)*np.log(1-y_hat) )except:return float('inf')def dJ(theta,X_b,y):return X_b.T.dot(self._sigmoid(X_b.dot(theta))-y)def gradient_descent(initia_theta,X_b,y, eta,n_iters =1e4,epsilon =1e-8 ):theta = initia_thetacur_iter = 0while cur_iter < n_iters:gradient = dJ(theta,X_b, y)last_theta = thetatheta = theta - eta * gradientif (abs(J(theta,X_b, y)-J(last_theta,X_b, y)) < epsilon):breakcur_iter += 1return thetaX_b = np.hstack([np.ones(len(X_train)).reshape(-1,1),X_train])initia_theta = np.zeros(X_b.shape[1])self._theta = gradient_descent(initia_theta,X_b,y_train,eta,n_iters)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef predict_proba(self,X_predict):X_b = np.hstack([np.ones(len(X_predict)).reshape(-1,1),X_predict])return self._sigmoid(X_b.dot(self._theta))def predict(self,X_predict):proba = self.predict_proba(X_predict)return np.array(proba >= 0.5,dtype = 'int')def score(self,X_test,y_test):y_predict = self.predict(X_test)return accuracy_score(y_test, y_predict)def __repr__(self):return "LogisticRegression()"
可视化划分:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
plot_decision_boundary(log_reg,X_test)
plt.scatter(X_test[y_test==0,0],X_test[y_test==0,1])
plt.scatter(X_test[y_test==1,0],X_test[y_test==1,1])
plt.show()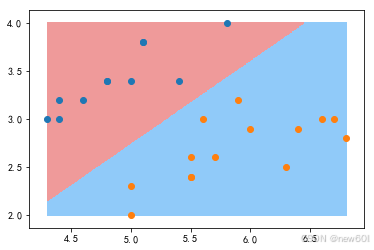
总结
注意:虽然 Logistic 回归的名字叫作回归,但其实它是一种分类方法!!!
优点
- 逻辑斯蒂回归模型基于简单的线性函数,易于理解和实现。
- Logistic 回归模型对一般的分类问题都可使用。
- Logistic 回归模型不仅可以预测出样本类别,还可以得到预测为某类别的近似概率,这在许多需要利用概率辅助决策的任务中比较实用。
- Logistic 回归模型中使用的对数损失函数是任意阶可导的凸函数,有很好的数学性质,可避免局部最小值问题。
缺点
- Logis ic 回归模型本质上还是种线性模型,只能做线性分类,不适合处理非线性的情况,一般需要结合较多的人工特征处理使用。
- Logistic 回归对正负样本的分布比较敏感,所以要注意样本的平衡性,即y=1的样本数不能太少。
- 模型不能自动捕捉特征之间的交互作用,需要手动进行特征工程。






![[Git][认识Git]详细讲解](https://i-blog.csdnimg.cn/direct/4f03a191b5b44f5d8bdf70d5ba418ca1.png)











