IDL=indexed double list
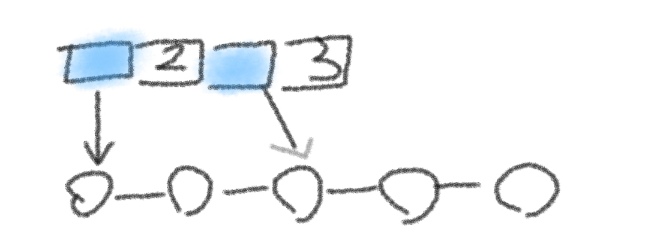
如图,下方是一个双链表,上方是索引。索引储存为结构体数组,结构体内包括一个指针,和长度。
假设索引只有一个,这时,它应该指向双链表的中间,这样才能提高搜索效率。称为1/2索引。
索引数增加到两个,它们应该指向1/3处。
索引数为N,指向1/(N+1)处。
经过上述设计后,索引速度不会达到O(logn),但是却能提高不少。
设双链表的最大长度为100万,则索引长1000,每个索引项中的长度为1000。即,隔一千多项有一个指针。
增加数据时,重新计算索引数组中的指针和长度,这需要产生2K次修改。相比使用数组,对于有1M个元素的数组,在首部增加1项,会产生1M个数据移动。2K比1M小很多。
举例来说,索引中储存的长度是6-6-5-6,插入一项之后变成6-7-5-6。总长度为24,分4段,平均每段长度为6,所以,修改为6-6-6-6。这一过程可以叫做“索引的均衡化”。
查找数据时,在索引数组中采用二分法,先找到双链表的中间位置,比大小。然后在前半段或后半段之中继续查找。当索引数组中的前后两项相邻时,就启用双链表的遍历,一项接一项地查找。
上文中计算过,隔一千个元素有一个索引,所以,遍历的过程会持续1000次。这仍然比遍历整个双链表的100万次小很多。
总之,带索引的双链表和跳表相比,它们都能维持序列,进行范围搜索。IDL占用的空间比跳表少,速度也慢,这是“空间换时间”策略的折中方案。
之前的博客描述过“延迟序列”,这是另一个处理序列的方案。它更省内存,可以用于从内存里的红黑树,到硬盘上的数据结构(如B+树),的转换过程中的替代品。但是延迟序列不能访问相邻元素,IDL却可以。