排序算法：冒泡排序，golang实现

前言

冒泡排序

代码示例

1. 算法包

2. 冒泡排序代码

3. 模拟排序

4. 运行程序

5. 从大到小排序

循环细节

外层循环

内层循环

总结

循环次数测试

假如 10 条数据进行排序

假如 20 条数据进行排序

假如 30 条数据进行排序

假设 5000 条数据，对比选择、插入、快速、堆、归并

冒泡排序的适用场景

1. 数据量非常小

2. 数据几乎有序

3. 教学用途

4. 稳定性

前言

在实际场景中，选择合适的排序算法对于提高程序的效率和性能至关重要，本节课主要讲解"冒泡排序"的适用场景及代码实现。

冒泡排序

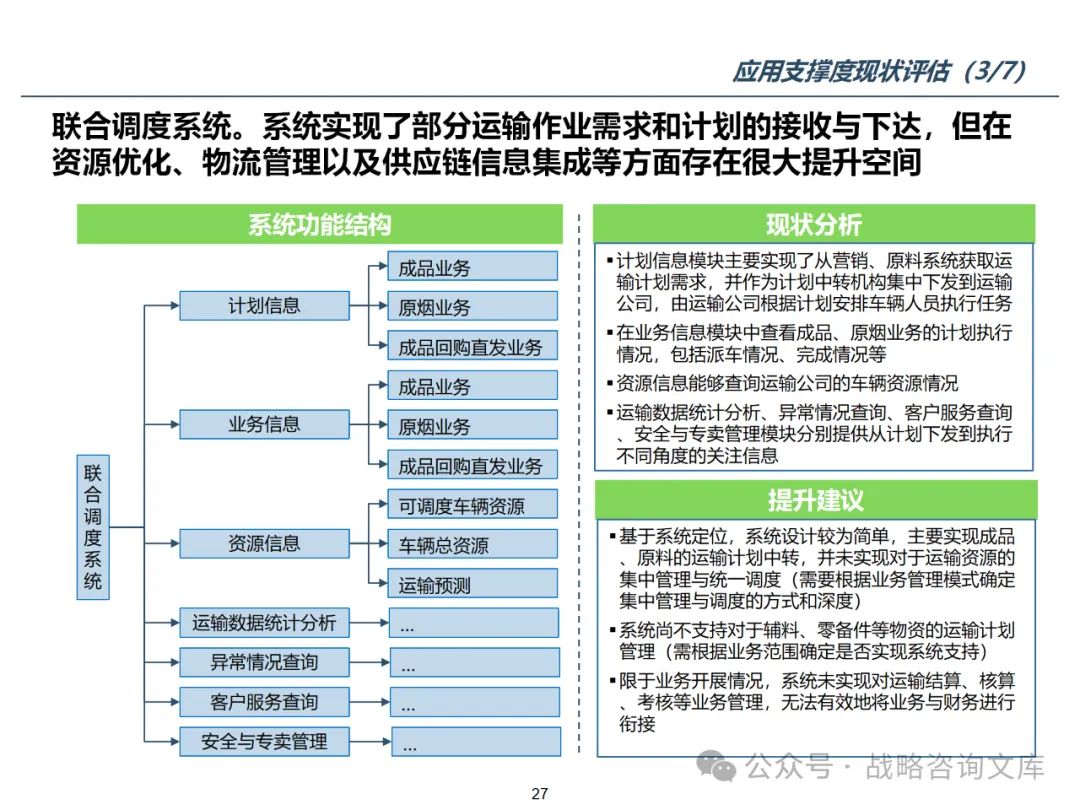
冒泡排序(Bubble Sort) 是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小(或越大)的元素会经由交换慢慢"浮"到数列的顶端。

代码示例

下面我们使用Go语言实现一个冒泡排序：

1. 算法包

创建一个 pkg/algorithm.go

touch pkg/algorithm.go

2. 冒泡排序代码

打开 pkg/algorithm.go 文件，代码如下

从小到大 排序

package pkg// BubbleSort 冒泡排序
func BubbleSort(arr []int) {n := len(arr)              // 获取切片长度for i := 0; i < n-1; i++ { // 外层循环控制遍历的次数for j := 0; j < n-i-1; j++ { // 内层循环控制每轮遍历的次数，每完成一轮，最大数就“冒泡”到最后if arr[j] > arr[j+1] { // 比较相邻元素，如果前一个比后一个大，则交换arr[j], arr[j+1] = arr[j+1], arr[j] // 两个元素换位置}}}
}

3. 模拟排序

打开 main.go 文件，代码如下：

package mainimport ("demo/pkg""fmt"
)func main() {// 定义一个切片，这里我们模拟 10 个元素arr := []int{999, 452, 37, 1573, 234, 5, 318, 76483, 115, 86}fmt.Println("Original data:", arr) // 先打印原始数据pkg.BubbleSort(arr)                // 调用冒泡排序fmt.Println("New data:  ", arr)    // 后打印排序后的数据
}

4. 运行程序

打开终端，我们运行 go ：

go run main.go

能发现， Original data 后打印的数据，正是我们代码中定义的切片数据，顺序也是一致的。

New Data 后打印的数据，则是经过冒泡排序后的数据，是从小到大的。

5. 从大到小排序

如果需要从大到小排序也是可以的，在代码里，将两个元素比较的大于符号改成小于符号即可。

修改 pkg/algorithm.go 文件：

package pkg// BubbleSort 冒泡排序
func BubbleSort(arr []int) {n := len(arr)              // 获取切片长度for i := 0; i < n-1; i++ { // 外层循环控制遍历的次数for j := 0; j < n-i-1; j++ { // 内层循环控制每轮遍历的次数，每完成一轮，最大数就“冒泡”到最后if arr[j] < arr[j+1] { // 比较相邻元素，如果前一个比后一个大，则交换arr[j], arr[j+1] = arr[j+1], arr[j] // 两个元素换位置}}}
}

只需要一丁点的代码即可

在第八行代码中，我们将 ">" 改成了 "<" ，这样就变成了从大到小排序了

循环细节

心细的同学已经发现，我们的外层循环中，有 "n - 1"，而内层循环中，有 "n - i - 1"

外层循环

外层循环控制的是遍历数组的总轮数。在冒泡排序中，没完成一轮遍历，都会确保至少有一个元素被放置到它最终的位置上。因此，随着排序的进行，未排序的元素数量逐渐减少。

初始时，未排序的元素是整个数组，长度为 n
第一轮遍历后，最大的元素被放到了数组的最后一位，因此未排序的元素减少了一个，剩下 n - 1 个
第二轮遍历后，第二大的元素被放到了倒数第二个，未排序的元素再减少一个，剩下 n - 2 个
以此类推，直到所有的元素都排序完成

因此，外层循环的次数是 n - 1，即

for i := 0; i < n - 1; i ++ {}

内层循环

内层循环负责在每一轮遍历中，通过相邻元素的比较和交换，将未排序部分的最大元素"冒泡"到其正确位置。随着外层循环的进行，每一轮结束后，数组的末尾都会增加一个已排序的元素(即最大元素)，因此内层循环的遍历范围需要相应减少。

初始时，内层循环需要遍历整个未排序的数组，即 j 从 0 到 n - 1。但由于每次遍历结束时，最后一个元素都会是未排序部分的最大值，所以实际上内层循环只需要遍历到 n - 2 (因为最后一个元素已经是最大的了，无需再比较)
随着外层循环的进行(即 i 的增加)，每一轮结束时，数组的末尾都会增加一个已排序的元素，因此，每进入下一轮外层循环，内层循环的遍历范围就可以减少一个元素，即 n - i - 1

综上，内层循环的条件是