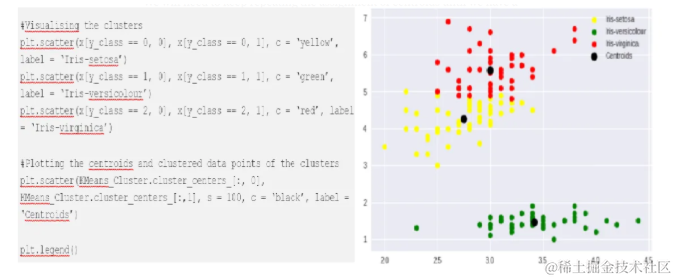
LeetCode2368 受限条件下可到达节点的数目

 

 

 

class Solution {
public:int dfs(vector<vector<int>>& g,int x,int fa){int sum=1;for(int y:g[x]){if(y!=fa) sum+=dfs(g,y,x);}return sum;}int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {vector<vector<int>> g(n);unordered_set<int> s;for(int i=0;i<restricted.size();i++) s.insert(restricted[i]);for(int i=0;i<edges.size();i++){int x=edges[i][0],y=edges[i][1];if(!s.count(x)&&!s.count(y)){//两节点都不受限才建立边g[x].push_back(y);g[y].push_back(x);}}return dfs(g,0,-1);}
};

时间复杂度：O(n)

空间复杂度：O(n) 

LeetCode2477 到达首都的最少油耗（贡献法）

 

/** @lc app=leetcode.cn id=2477 lang=cpp** [2477] 到达首都的最少油耗*/// @lc code=start
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;class Solution {
public:long long res=0;int sum=0;int dfs(vector<vector<int>>& g,int x,int fa,int seats){int sum=1;for(int y:g[x]){if(y!=fa){ //递归子节点，不能递归父节点sum+=dfs(g,y,x,seats); //统计子树大小}}if(x!=0) //x不是根节点res+=(sum-1)/seats+1; //ceil(sum*1.0/seats); return sum;}long long minimumFuelCost(vector<vector<int>>& roads, int seats) {int n=roads.size()+1;vector<vector<int>> g(n);for(int i=0;i<roads.size();i++){int from=roads[i][0],to=roads[i][1];g[from].push_back(to);g[to].push_back(from);}dfs(g,0,-1,seats);return res;}
};

时间复杂度：O(n)

空间复杂度：O(n)